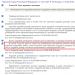
The magnitude of the regression coefficient shows the average change. Types of regression models

In the presence of correlations between factor and effective features, doctors often have to be installed, for which magnitude the value of one attribution can change when the other is changed by the generally accepted or established by the researcher himself.

For example, how the mass of the 1st class schoolchildren (girls or boys) changes, if they increase them by 1 cm. For these purposes, the regression analysis method is applied.

Most often, the regression analysis method is used to develop regulatory scales and physical development standards.

1. Definition of regression. Regression is a function that allows one characteristic of a single sign to determine the average value of another feature, correlatedly related to the first.

   For this purpose, the regression coefficient and a number of other parameters are applied. For example, you can calculate the number of colds on average at certain values \u200b\u200bof the average monthly air temperature in the autumn-winter period.

2. Definition of the regression coefficient. The regression coefficient is an absolute value on which the value of one sign changes when the other associated feature is changed to the established unit of measurement.
3. The formula of the regression coefficient. R y / x \u003d r x x (σ y / σ x)
   where R y / x is the regression coefficient;
   r Hu - the correlation coefficient between signs x and y;
   (Σ y and Σ x) - the rms deviations of the signs of X and y.

   In our example;
   Σ x \u003d 4.6 (the rms deviation of the air temperature in the autumn-winter period;
   Σ y \u003d 8.65 (the rms deviation of the number of infectious-colds).
   Thus, R y / X is the regression coefficient.
   R y / x \u003d -0.96 x (4.6 / 8.65) \u003d 1.8, i.e. When the average monthly air temperature (x) is reduced by 1 degree, the average number of infectious-colds (y) in the autumn-winter period will vary by 1.8 cases.

4. Regression equation. y \u003d m y + r y / x (x - m x)
   where y is the average sign that should be determined by changing the average value of another feature (x);
   x - the famous average value of another sign;
   R y / x is the regression coefficient;
   M X, M y - famous averages of signs X and y.

   For example, the average number of infectious-colds (y) can be determined without special measurements at any average value of the average air temperature (x). So, if x \u003d - 9 °, r y / x \u003d 1.8 diseases, m x \u003d -7 °, m y \u003d 20 diseases, then y \u003d 20 + 1.8 x (9-7) \u003d 20 + 3 , 6 \u003d 23.6 diseases.
   This equation is used in the case of a straight line between two signs (x and y).

5. Purpose of the regression equation. The regression equation is used to build a regression line. The latter allows without special measurements to determine any average value (y) of one character, if the value (x) of another feature changes. According to this data, a schedule is built - regression linewhere the average number of colds can be determined in any meaning of the average temperature in the limits between the calculated values \u200b\u200bof the number of colds.
6. Regression Sigma (Formula).
   where σ r / x - sigma (rms deviation) regression;
   Σ y - the standard deviation of the feature of the
   r Hu is the correlation coefficient between signs x and y.

   So, if σ y is the standard deviation of the number of colds \u003d 8.65; R Hu is the correlation coefficient between the number of colds (y) and the average monthly air temperature in the autumn-winter period (x) is 0.96,

   

7. Appointment of regression sigma. Gives a characteristic measure of a variety of productive feature (y).

   For example, characterizes the diversity of the number of colds with a certain meaning of the average monthly air temperature in the autumn-winter period. Thus, the average number of colds at air temperature X 1 \u003d -6 ° can range from 15.78 diseases to 20.62 diseases.
   At x 2 \u003d -9 °, the average number of colds may vary in the range of 21.18 diseases to 26.02 diseases, etc.

   Regression sigma is used in constructing a regression scale, which reflects the deviation of the quantity of an effective feature from the average value deflected on the regression line.

8. Data required for calculating and graphic image regression scales
   • regression coefficient - R y / x;
   • regression equation - y \u003d m y + r y / x (x - m x);
   • regression Sigma - Σ RX / Y
9. Sequence of calculations and graphic image Regression scales.
   • determine the regression coefficient by the formula (see paragraph 3). For example, it should be determined how much the body weight is changed (at a certain age, depending on the floor), if the average growth will change by 1 cm.
   • according to the formula of the regression equation (see p. 4), determine which will be on average, for example, body weight (y, in 2, in 3 ...) * for a certain growth value (x, x 2, x 3 ...) .
     ________________
     * The magnitude of "y" should count no less than three known values \u200b\u200bof "X".

     At the same time, the average values \u200b\u200bof body mass and growth (M X, and M) for a certain age and gender are known

   • calculate regression sigma, knowing the corresponding values \u200b\u200bof σ y and r x and substituting their values \u200b\u200bin the formula (see paragraph 6).
   • based on the known values \u200b\u200bof x 1, x 2, x 3 and corresponding to the mean values \u200b\u200bof 1, in 2 in 3, as well as the smallest (y - σ r / x) and the largest (y + σ r / x) values \u200b\u200b(y) Build a regression scale.

     For a graphic image, the regression scale on the graph is first noted by the values \u200b\u200bof x, x 2, x 3 (ordinate axis), i.e. Regression line is built, such as body weight (y) dependence (X).

     Then at the appropriate points in 1, Y 2, Y 3, the numerical values \u200b\u200bof the regression sigma are noted, i.e. The graph find the smallest and most values \u200b\u200bof 1, y 2, y 3.

10. Practical use of regression scales. Regulatory scales and standards are being developed, in particular in physical development. According to the standard scale, it is possible to give an individual assessment of the development of children. At the same time, physical development is estimated as harmonious, if, for example, with a certain growth, the mass of the child's body is within one regression sigma to the average calculated unit of body weight - (y) for this growth (x) (in ± 1 σ Ry / x).

    Physical development is considered disharmonious by weight of the body if the mass of the child's body for a certain growth is within the second regression sigma: (y ± 2 σ Ry / x)

    Physical development will be sharply disharmonious both due to excess and due to insufficient body weight, if the body weight for a certain growth is within the third regression sigma (y ± 3 σ Ry / x).

According to the results of a statistical study of the physical development of boys for 5 years, it is known that their average growth (X) is equal to 109 cm, and the average body weight (y) is equal to 19 kg. The correlation coefficient between rising and body weight is +0.9, the average quadratic deviations are presented in the table.

Requires:

• calculate the regression coefficient;
• according to the regression equation, determine which expected mass of the boys body of 5 years with growth, equal to x1 \u003d 100 cm, x2 \u003d 110 cm, x3 \u003d 120 cm;
• calculate regression sigma, to build a regression scale, the results of its decision to submit graphically;
• make appropriate conclusions.

The condition of the task and the results of its solutions are presented in a summary table.

Table 1

Conditions of the problem				The results of the solution of the problem
				regression equation			sigma Regression	regression scales (expected body weight (kg))
	M.	σ	r Hu.	R y / x	h.	W.	Σ R x / y	y - σ r / x	y + Σ r / x
1	2	3	4	5	6	7	8	9	10
Growth (x)	109 cm	± 4.4cm	+0,9	0,16	100cm	17.56 kg	± 0.35 kg	17,21 kg	17.91 kg
Body Mass (Y)	19 kg	± 0.8 kg			110 cm	19,16 kg		18.81 kg	19,51 kg
					120 cm	20.76 kg		20.41 kg	21.11 kg

Decision.

Output. Thus, the regression scale within the calculated amount of body weight allows it to determine it with any other value of growth or evaluate the individual development of the child. To do this, restore perpendicular to the regression line.

1. Vlasov V.V. Epidemiology. - M.: Gootar-Honey, 2004. - 464 p.
2. Lisitsyn Yu.P. Public health and healthcare. Textbook for universities. - M.: Goeotar-Honey, 2007. - 512 p.
3. Medica V.A., Yuriev V.K. Course of public health and health lectures: part 1. Public health. - M.: Medicine, 2003. - 368 p.
4. Minaev V.A., Vishnyakov N.I. and others. Social Medicine and Health Organization (Guidelines in 2 volumes). - St. Petersburg, 1998. -528 p.
5. Kucherenko V.Z., Agarkov N.M. and other healthy hygiene and the organization of health (Tutorial) - Moscow, 2000. - 432 p.
6. S. Glanz. Medical and biological statistics. Per with English. - M., Practice, 1998. - 459 p.

Using a graphic method.
This method is used for a visual image of the form of communication between the economic indicators studied. To do this, in a rectangular coordinate system, a graph is built, the individual values \u200b\u200bof the resultant animal are deposited along the axis of the ordinate, and according to the abscissa axis, the individual values \u200b\u200bof the factor of X.
The combination of points of productive and factor signs is called field of correlation.
Based on the correlation field, you can hypothesize (for the general aggregate) that the relationship between all possible values \u200b\u200bX and Y is linear.

Linear regression equation It has the form Y \u003d BX + A + ε
Here ε is a random error (deviation, indignation).
Causes of the existence of a random error:
1. Included in the regression model of significant explanatory variables;
2. Aggregation of variables. For example, the function of total consumption is an attempt to generally express the set of solutions of individual individuals about expenditures. It is only an approximation of individual relations that have different parameters.
3. Incorrect description of the model structure;
4. Incorrect functional specification;
5. Measurement errors.
Since deviations ε i for each specific observation I - random and their values \u200b\u200bare unknown in the sample, then:
1) According to the observations of X I and Y I, it is possible to obtain only estimates of the parameters α and β
2) estimates of the parameters α and β regression model are respectively the values \u200b\u200bof A and B, which are random character, because correspond to random sample;
Then the estimated regression equation (built according to selective data) will have the form y \u003d bx + a + ε, where E i is the observed values \u200b\u200b(estimates) of errors ε i, a and b, respectively, the estimates of the parameters α and β regression model to be found.
To estimate the parameters α and β, MNA is used (the least squares method).
System of normal equations.

For our data, the system of equations is:

10A + 356B \u003d 49
356A + 2135B \u003d 9485

From the first equation, express a and substitute to the second equation
We get b \u003d 68.16, a \u003d 11.17

Regression equation:
y \u003d 68.16 x - 11.17

1. Parameters of the regression equation.
Selective average.



Selective dispersions.


Radial deviation

1.1. Correlation coefficient
Calculate the indicator of the tightness of the connection. This indicator is the selective linear correlation coefficient, which is calculated by the formula:

The linear correlation coefficient takes values \u200b\u200bfrom -1 to +1.
Communication between features may be weak and strong (close). Their criteria are estimated on the sampler scale:
0.1 < r xy < 0.3: слабая;
0.3 < r xy < 0.5: умеренная;
0.5 < r xy < 0.7: заметная;
0.7 < r xy < 0.9: высокая;
0.9 < r xy < 1: весьма высокая;
In our example, the relationship between the sign Y factor X is very high and straight.

1.2. Regression equation (Evaluation of the regression equation).

The linear regression equation has the form y \u003d 68.16 x -11.17
The coefficients of the linear regression equation can be given an economic meaning. The coefficient of the regression equation Shows how much units. The result will change when the factor is changed per unit.
The coefficient B \u003d 68.16 shows the average change in the effective indicator (in units of measurement y) with an increase or decrease in the value of the factor x per unit of its measurement. In this example, with an increase of 1, Y rises by an average of 68.16.
The coefficient A \u003d -11.17 formally shows the predicted level of y, but only if x \u003d 0 is close to selective values.
But if x \u003d 0 is far from selective values \u200b\u200bx, then the literal interpretation can lead to incorrect results, and even if the regression line quite accurately describes the values \u200b\u200bof the observed sample, there is no warranty, which will also be with extrapolation to the left or right.
Substituting the corresponding X values \u200b\u200bin the regression equation, you can define aligned (predicted) values \u200b\u200bof the effective indicator Y (x) for each observation.
The relationship between y and x defines the regression coefficient B (if\u003e 0 is a direct connection, otherwise - reverse). In our example, the connection is straight.

1.3. The coefficient of elasticity.
Regression coefficients (in Example b) undesirable to use for the direct assessment of the influence of factors on a productive basis in the event that there is a difference in units of measurement of the effective indicator and factor of X.
For these purposes, the coefficients of elasticity and beta are calculated - coefficients. The coefficient of elasticity is by the formula:


It shows how much percent an average of the result is a result of a factor of X by 1%. It does not take into account the degree of broadcability of factors.
In our example, the coefficient of elasticity is more than 1. Consequently, with a change in X by 1%, y will change by more than 1%. In other words - x significantly affects Y.
Beta - coefficient It shows which part of the value of its average quadratic deviation will change on average the value of the effective feature when the factor of the sign is changed by the value of its standard deviation at a fixed level at a constant value of the remaining independent variables:

Those. An increase in x by the value of the rms deviation of this indicator will lead to an increase in the average Y at 0.9796 of the standard deviation of this indicator.

1.4. Approximation error.
We estimate the quality of the regression equation using an absolute approximation error.


Since the error is more than 15%, then this equation is not desirable to use as regression.

1.6. The coefficient of determination.
The quadrant (multiple) correlation coefficient is called a determination coefficient, which shows the share of the variation of the productive feature explained by the variation of a factor of the sign.
Most often, giving the interpretation of the determination coefficient, it is expressed as a percentage.
R 2 \u003d 0.98 2 \u003d 0.9596
those. In 95.96% of cases of change X lead to a change in. In other words - the accuracy of the selection of the regression equation is high. The remaining 4.04% changes y are explained by factors not accounted for in the model.

X.	Y.	x 2	Y 2.	X Y.	y (x)	(Y i -y Cp) 2	(Y-y (x)) 2	(X i -X CP) 2	| y - y x |: y
0.371	15.6	0.1376	243.36	5.79	14.11	780.89	2.21	0.1864	0.0953
0.399	19.9	0.1592	396.01	7.94	16.02	559.06	15.04	0.163	0.1949
0.502	22.7	0.252	515.29	11.4	23.04	434.49	0.1176	0.0905	0.0151
0.572	34.2	0.3272	1169.64	19.56	27.81	87.32	40.78	0.0533	0.1867
0.607	44.5	.3684	1980.25	27.01	30.2	0.9131	204.49	0.0383	0.3214
0.655	26.8	0.429	718.24	17.55	33.47	280.38	44.51	0.0218	0.2489
0.763	35.7	0.5822	1274.49	27.24	40.83	61.54	26.35	0.0016	0.1438
0.873	30.6	0.7621	936.36	26.71	48.33	167.56	314.39	0.0049	0.5794
2.48	161.9	6.17	26211.61	402	158.07	14008.04	14.66	2.82	0.0236
7.23	391.9	9.18	33445.25	545.2	391.9	16380.18	662.54	3.38	1.81

2. Assessment of parameters of the regression equation.
2.1. The significance of the correlation coefficient.

According to the Student table with the level of importance α \u003d 0.05 and the degrees of freedom k \u003d 7 we find T Crete:
t Crete \u003d (7; 0.05) \u003d 1.895
where m \u003d 1 is the number of explanatory variables.
If T Navel\u003e T critic, the resulting value of the correlation coefficient is recognized as significant (zero hypothesis that approves the equality zero correlation coefficient is rejected).
Since T Navel\u003e T Crete, we deflect the hypothesis of the equality 0 of the correlation coefficient. In other words, the correlation coefficient is statistically - significant
In the paired linear regression T 2 R \u003d T 2 B and then checking the hypotheses on the significance of regression coefficients and correlation is equivalent to testing the hypothesis about the materiality of the linear regression equation.

2.3. Analysis of the accuracy of determining estimates of regression coefficients.
The indispensable estimate of the dispersion of perturbations is the value:


S 2 Y \u003d 94.6484 is an inexplicable dispersion (measure of scattering by a dependent variable around the regression line).
S Y \u003d 9.7287 - Standard Error Evaluation (Standard Regression Error).
S A - standard deviation of a random variable a.


S b - standard deviation of a random value b.

2.4. Trust intervals for the dependent variable.
Economic forecasting based on a constructed model assumes that the previously existing relationships of variables are preserved and for the period of protection.
To predict the dependent variable of the effective feature, it is necessary to know the projected values \u200b\u200bof all the factors included in the model.
Forecast values \u200b\u200bof factors are substituted into the model and receive point forecast estimates of the studied indicator. (A + BX P ± ε)
where

Calculate the boundaries of the interval in which 95% of possible values \u200b\u200bof Y will be concentrated with an unlimited large number of observations and x p \u003d 1 (-11.17 + 68.16 * 1 ± 6.4554)
(50.53;63.44)

Individual confidence intervals forY. With this meaning X..
(A + BX I ± ε)
where

X I.	y \u003d -11.17 + 68.16x i	ε I.	y min	y Max
0.371	14.11	19.91	-5.8	34.02
0.399	16.02	19.85	-3.83	35.87
0.502	23.04	19.67	3.38	42.71
0.572	27.81	19.57	8.24	47.38
0.607	30.2	19.53	10.67	49.73
0.655	33.47	19.49	13.98	52.96
0.763	40.83	19.44	21.4	60.27
0.873	48.33	19.45	28.88	67.78
2.48	158.07	25.72	132.36	183.79

With a probability of 95%, it can be guaranteed that the values \u200b\u200bof Y with an unlimited large number of observations will not be out of the interval found.

2.5. Checking the hypothesis relative to the coefficients of the regression linear equation.
1) T-statistics. Student's criterion.
We check the hypothesis H 0 on the equality of individual regression coefficients zero (with an alternative H 1 is not equal to) at the level of significance α \u003d 0.05.
t Crete \u003d (7; 0.05) \u003d 1.895


Since 12.8866\u003e 1.895, the statistical significance of the regression coefficient B is confirmed (reject the hypothesis of the equality zero of this coefficient).


Since 2.0914\u003e 1.895, the statistical significance of the regression coefficient A is confirmed (reject the hypothesis of the equality zero of this coefficient).

Trust interval for the coefficients of the regression equation.
We define the confidence intervals of regression coefficients, which with a reliability of 95% will be as follows:
(B - T Crete S B; B + T Crete S B)
(68.1618 - 1.895 5.2894; 68.1618 + 1.895 5.2894)
(58.1385;78.1852)
With a probability of 95%, it can be argued that the value of this parameter will lie in the found interval.
(A - T a)
(-11.1744 - 1.895 5.3429; -11.1744 + 1.895 5.3429)
(-21.2992;-1.0496)
With a probability of 95%, it can be argued that the value of this parameter will lie in the found interval.

2) F-statistics. Fisher's criterion.
Verification of the significance of the regression model is carried out using the Fisher's F-criterion, the calculated value of which is as the ratio of the dispersion of the original series of observations of the studied indicator and the unbelievable estimate of the residual sequence dispersion for this model.
If the calculated value with Lang \u003d EN-US\u003e N-M-1) degrees of freedom is more tabular at a given level of significance, the model is considered significant.

where M is the number of factors in the model.
Assessment of the statistical significance of pair linear regression is made according to the following algorithm:
1. The zero hypothesis is put forward that the equation generally is statistically insignificant: H 0: R 2 \u003d 0 at the level of significance α.
2. Further define the actual value of the F-criterion:


where m \u003d 1 for paired regression.
3. A table value is determined by the Fisher Distribution Tables for a given level of significance, taking into account that the number of freedom degrees for the total sum of squares (greater dispersion) is 1 and the number of degrees of freedom of the residual sum of squares (less dispersion) with linear regression is N-2 .
4. If the actual value of the F-criterion is less tabular, then it is said that there is no reason to deflect the zero hypothesis.
Otherwise, the zero hypothesis deviates and with a probability (1-α) an alternative hypothesis on the statistical significance of the equation as a whole is adopted.
Table value of the criterion with degrees of freedom k1 \u003d 1 and k2 \u003d 7, FKP \u003d 5.59
Since the actual value of F\u003e FKP, the determination coefficient is statistically significant (the estimate of the regression equation is statistically reliable).

Check for autocorrelation residues.
An important prerequisite for building a high-quality regression model on MNA is the independence of the values \u200b\u200bof random deviations from deviation values \u200b\u200bin all other observations. This ensures the absence of correlated between any deviations and, in particular, between adjacent deviations.
Autocorrelation (consistent correlation) It is defined as a correlation between the observed indicators, ordered in time (time series) or in space (cross-rows). The autocorrelation of residues (deviations) is usually found in regression analysis when using time series data and very rarely when using cross-data.
In economic tasks, it is much more common positive autocorrelationthan negative autocorrelation. In most cases, positive autocorrelation is caused by the directional constant influence of some of the factors unaccounted in the model.
Negative autocorrelation In fact, means that a positive deflection follows a negative and vice versa. Such a situation may occur if the same relationship between the demand for refreshments and income is considered for seasonal data (winter-summer).
Among the main reasons causing autocorrelationYou can select the following:
1. Errors specification. It will not be accepted in the model of any important explaining variable or incorrect choice of the form of addiction usually lead to systemic deviations of observation points from the regression line, which can cause autocorrelation.
2. Inertia. Many economic indicators (inflation, unemployment, GNP, etc.) have a certain cyclicity associated with the conversion of business activity. Therefore, the change in the indicators does not occur instantly, but has a certain inertness.
3. Effect of web. In many industrial and other areas, economic indicators react to a change in economic conditions with delay (temporary lag).
4. Smoothing data. Often, data for some long-lasting time period is obtained by averaging data on the components of its intervals. This can lead to a certain smoothing of oscillations that were used within the period under consideration, which in turn can be the cause of autocorrelation.
The consequences of autocorrelation are similar to the consequences of heterosadasticity: conclusions for T- and F-Statistics, which determine the significance of the regression coefficient and the coefficient of determination, may be incorrect.

Autocorrelation detection

1. Graphic method
There are a number of graphic definition of autocorrelation. One of them links deviations E i with the moments of their preparation I. At the same time, along the abscissa axis, either the receipt of statistical data is postponed or the sequence number of observation, and along the ordinate axis deviations E I (or deviation assessment).
It is natural to assume that if there is a certain connection between deviations, the autocorrelation takes place. The lack of dependence will soon indicate the absence of autocorrelation.
Autocorrelation becomes more visual if you construct a graph of E I from E i-1.

Darbina Watson's Criterion.
This criterion is the most famous for the detection of autocorrelation.
With statistical analysis of the regression equation at the initial stage, the feasibility of one prerequisite is often checked: conditions of statistical independence of deviations among themselves. In this case, the incorrectness of the neighboring values \u200b\u200bof E i is checked.

Y.	y (x)	E i \u003d y-y (x)	E 2.	(E i - E I-1) 2
15.6	14.11	1.49	2.21	0
19.9	16.02	3.88	15.04	5.72
22.7	23.04	-0.3429	0.1176	17.81
34.2	27.81	6.39	40.78	45.28
44.5	30.2	14.3	204.49	62.64
26.8	33.47	-6.67	44.51	439.82
35.7	40.83	-5.13	26.35	2.37
30.6	48.33	-17.73	314.39	158.7
161.9	158.07	3.83	14.66	464.81
			662.54	1197.14

Darbina Watson statistics are used to analyze the correlation of deviationsons:

Critical values \u200b\u200bD 1 and D 2 are determined based on special tables for the required level of significance α, the number of observations N \u003d 9 and the number of explanatory variables M \u003d 1.
Autocorrelation is absent if the following condition is satisfied:
d 1.< DW и d 2 < DW < 4 - d 2 .
Without referring to the tables, you can use the approximate rule and assume that the autocorrelation of the residues is absent if 1.5< DW < 2.5. Для более надежного вывода целесообразно обращаться к табличным значениям.

The regression coefficient is an absolute value on which the value of one sign changes when the other associated feature is changed to the established unit of measurement. Definition of regression. The relationship between y and x defines the regression coefficient B (if\u003e 0 is a direct connection, otherwise - reverse). The linear regression model is often used and the most studied in the econometric.

1.4. Error approximation. The quality of the regression equation using an absolute approximation error. Forecast values \u200b\u200bof factors are substituted into the model and receive point forecast estimates of the studied indicator. Thus, regression coefficients characterize the degree of importance of individual factors to increase the level of productivity.

Recession coefficient

Consider now the task 1 from the tasks on the regression analysis given on p. 300-301. One of the mathematical results of the theory of linear regression says that the estimate N is an unformed assessment with a minimum dispersion in the class of all linear unrelated estimates. For example, you can calculate the number of colds on average at certain values \u200b\u200bof the average monthly air temperature in the autumn-winter period.

Regression line and regression equation

Regression sigma is used in constructing a regression scale, which reflects the deviation of the quantity of an effective feature from the average value deflected on the regression line. 1, x2, x3 and corresponding to the average values \u200b\u200bof U1, U2 U3, as well as the smallest (y - σru / x) and the largest (y + σr / x) values \u200b\u200b(y) build the regression scale. Output. Thus, the regression scale within the calculated amount of body weight allows it to determine it with any other value of growth or evaluate the individual development of the child.

In the matrix form, the regression equation (SD) is written in the form: Y \u003d BX + U (\\ DisplayStyle Y \u003d BX + U), where U (\\ displayStyle U) is the error matrix. The statistical use of the word "regression" comes from a phenomenon known as regression to the average attributed to Sir Francis Galton (1889).

Paired linear regression can be expanded by including more than one independent variable; In this case, it is known as multiple regression. And for emissions, and for "influential" observations (points), models are used, both with their inclusion, and without them, pay attention to the change in the assessment (regression coefficients).

Due to the linear relationship and we expect that it changes, as it changes, and call it a variation, which is due or explained by regression. If so, most of the variation will be explained by regression, and points will lie close to the regression line, i.e. The line is well consistent with the data. The difference is a percentage of a dispersion that cannot be explained by regression.

This method is used for a visual image of the form of communication between the economic indicators studied. Based on the correlation field, you can hypothesize (for the general aggregate) that the relationship between all possible values \u200b\u200bX and Y is linear.

The reasons for the existence of a random error: 1. Inclusion in the regression model of significant explanatory variables; 2. Aggregation of variables. System of normal equations. In our example, the connection is straight. To predict the dependent variable of the effective feature, it is necessary to know the projected values \u200b\u200bof all the factors included in the model.

Comparison of correlation and regression coefficients

With a probability of 95%, it can be guaranteed that the values \u200b\u200bof Y with an unlimited large number of observations will not be out of the interval found. If the calculated value with Lang \u003d EN-US\u003e N-M-1) degrees of freedom is more tabular at a given level of significance, the model is considered significant. This ensures the absence of correlated between any deviations and, in particular, between adjacent deviations.

Recession coefficients and their interpretation

In most cases, positive autocorrelation is caused by the directional constant influence of some of the factors unaccounted in the model. Negative autocorrelation actually means that the positive deflection follows a negative and vice versa.

What is regression?

2. Inertia. Many economic indicators (inflation, unemployment, GNP, etc.) have a certain cyclicity associated with the conversion of business activity. In many industrial and other areas, economic indicators react to a change in economic conditions with delay (temporary lag).

If pre-standardization of factor indicators has been carried out, then B0 is equal to the average value of the performance in the aggregate. The specific values \u200b\u200bof regression coefficients are determined by empirical data according to the least squares method (as a result of solving systems of normal equations).

The linear regression equation has the form y \u003d bx + a + ε here ε is a random error (deviation, indignation). Since the error is more than 15%, then this equation is not desirable to use as regression. Substituting the corresponding X values \u200b\u200bin the regression equation, you can define aligned (predicted) values \u200b\u200bof the effective indicator Y (x) for each observation.

What is regression?

Consider two continuous variables x \u003d (x 1, x 2, .., x n), y \u003d (y 1, y 2, ..., y n).

Place points on a two-dimensional scattering schedule and say that we have linear ratioIf the data is approximated by a straight line.

If we believe that y. depends on x., and change in y. are caused by changes in x.we can determine the regression line (regression y. on the x.), which best describes the straightforward ratio between these two variables.

The statistical use of the word "regression" proceeds from a phenomenon known as regression to the average attributed to Sir Francis Galton (1889).

He showed that, although high fathers tend to have high sons, the average growth of sons is less than that of their high fathers. The average growth of sons "regressing" and "moved" to the average growth of all fathers in the population. Thus, on average, high fathers have lower (but still high) sons, and low fathers have more high sons (but still rather low).

Regression line

The mathematical equation that estimates the line of simple (pair) linear regression:

x. called an independent variable or predictor.

Y. - Dependent variable or response variable. This value we expect for y. (on average) if we know the magnitude x.. it is "predicted meaning y.»

• a. - a free member (intersection) of the assessment line; This value Y.when x \u003d 0.(Fig.1).
• b. - angular coefficient or gradient of the estimated line; It is the value for which Y. increases on average if we increase x. per unit.
• a. and b. referred to the regression coefficients of the estimated line, although this term is often used only for b..

Paired linear regression can be expanded by including more than one independent variable; In this case, it is known as multiple regression.

Fig.1. Linear regression line showing the intersection A and angular coefficient B (increase of increment y with an increase in x per unit)

Least square method

We carry out regression analysis using the sample of observations, where a. and b. - selective estimates of true (general) parameters, α and β, which determine the linear regression line in the population (general aggregate).

The simplest method of determining coefficients a. and b. is an least square method (MNC).

Fit is estimated by considering the residues (vertical distance of each point from the line, for example, the residue \u003d observed y. - predicted y., Fig. 2).

The best adjustment line is chosen so that the sum of the squares of the residues was minimal.

Fig. 2. Linear regression line with depicted residues (vertical dotted lines) for each point.

Assumptions of linear regression

So, for each observed value, the residue is equal to the difference and the corresponding predicted each residue can be positive or negative.

You can use balances to verify the following assumptions underlying linear regression:

• Residues are normally distributed with zero average value;

If the assumptions of linearity, normality and / or constant dispersion are doubtful, we can transform or calculate the new regression line for which these assumptions are satisfied (for example, to use logarithmic transformation or other).

Anomalous values \u200b\u200b(emissions) and points of influence

"Influential" observation, if it is omitted, changes one or more estimates of the model parameters (i.e., an angular coefficient or a free member).

Emission (observation, which contradicts most values \u200b\u200bin the data set) can be "influential" observation and can well be detected visually, when examining a two-dimensional scattering diagram or residual graphics.

And for emissions, and for "influential" observations (points), models are used, both with their inclusion, and without them, pay attention to the change in the assessment (regression coefficients).

When analyzing, you should not discard emissions or points of influence automatically, since simple ignoring can affect the results obtained. Always study the reason for the appearance of these emissions and analyze them.

Linear regression hypothesis

When constructing a linear regression, a zero hypothesis is checked that the inner coefficient of the regression line β is zero.

If the angular coefficient of the line is zero, between and there is no linear ratio: the change does not affect

To test the zero hypothesis that the true angular coefficient is zero, you can use the following algorithm:

Calculate the statistics of the criterion equal to the ratio, which is subordinate to the distribution with degrees of freedom, where the standard error of the coefficient

,

- Evaluation of the dispersion of residues.

Usually if the achieved level of significance zero hypothesis deviates.

where the percentage of the distribution with the degrees of freedom that gives the likelihood of a bilateral criterion

This is the interval that contains an initial coefficient with a probability of 95%.

For large samples, let's say, we can approximate the value of 1.96 (that is, the statistics of the criterion will strive for normal distribution)

Quality assessment of linear regression: determination coefficient R 2

Due to the linear relationship and we expect that it changes, as it changes and call it a variation that is determined or explained by regression. The residual variation should be as small as possible.

If so, most of the variation will be explained by regression, and points will lie close to the regression line, i.e. The line is well consistent with the data.

Share of a general dispersion that is explained by regression called coefficient of determination, usually expressed through the percentage and designate R 2. (in pair linear regression is the value r 2., Correlation coefficient square), allows you to subjectively assess the quality of the regression equation.

The difference is a percentage of a dispersion that cannot be explained by regression.

There is no formal test for evaluation, we are forced to rely on a subjective judgment to determine the quality of the regression line fit.

Application of regression line for forecast

You can apply a regression line to predict the value value in the limit of the observed range (never extrapolarize outside of these limits).

We predict an average value for observable, which have a certain value by substituting this value to the regression line equation.

So, if we predict how to use this predicted value and its standard error to estimate the confidence interval for the true average value in the population.

Repetition of this procedure for different quantities allows you to build trust borders for this line. This is a band or area that contains a true line, for example, with a 95% trust probability.

Simple regression plans

Simple regression plans contain one continuous predictor. If there are 3 observations with the predictor values \u200b\u200bP, for example, 7, 4 and 9, and the plan includes the first-order effect P, the Matrix of the Plan X will be viewed

and the regression equation using P for X1 looks like

Y \u003d B0 + B1 P

If a simple regression plan contains a higher order effect for P, for example, a quadratic effect, then the values \u200b\u200bin the column X1 in the plan matrix will be erected into the second degree:

and the equation will take the form

Y \u003d B0 + B1 P2

Sigma-Recent and suprameryrized coding methods are not applied relative to simple regression plans and other plans containing only continuous predictors (since, there are simply no categorical predictors). Regardless of the selected coding method, the values \u200b\u200bof continuous variables increase to the appropriate degree and are used as values \u200b\u200bfor variables x. In this case, transcoding is not performed. In addition, when describing regression plans, you can omit the consideration of the matrix of the plan X, and work only with the regression equation.

Example: simple regression analysis

This example uses the data presented in Table:

Fig. 3. Table of source data.

Data is based on a comparison of correspondence of 1960 and 1970 in arbitrarily selected 30 districts. The names of the districts are presented in the form of observation names. Information on each variable is presented below:

Fig. 4. Table of variable specifications.

Task research

This example will analyze the poverty level correlation and the degree that predicts the percentage of families that are below the poverty line. Therefore, we will interpret the variable 3 (PT_POOR) as a dependent variable.

It is possible to push the hypothesis: a change in the population and the percentage of families that are below the poverty line are related. It seems reasonable to expect that poverty leads to the outflow of the population, therefore, there will be a negative correlation between the percentage of people beyond the poverty line and a change in population. Therefore, we will interpret the variable 1 (POP_CHNG) as a predictor variable.

View results

Recession coefficients

Fig. 5. Recessing coefficients PT_POOR on Pop_CHNG.

At the intersection of the POP_CHNG string and the pairs column. Not standardized coefficient for PT_POOR regression on Pop_CHNG is -0.40374. This means that for each decrease in population per unit, there is an increase in poverty level by .40374. Upper and lower (default) 95% confidence limits for this not standardized coefficient do not include zero, so the regression coefficient is significant at P level<.05 . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на.65.

Distribution of variables

Correlation coefficients can be significantly overestimated or understated if large emissions are present in the data. We study the distribution of the dependent variable PT_POOR in the counties. To do this, we construct a histogram of the PT_POOR variable.

Fig. 6. Histogram of the PT_POOR variable.

As you may notice, the distribution of this variable differs significantly from the normal distribution. Nevertheless, although even two districts (two right columns) have a high percentage of families who are below the poverty line than expected in the case of a normal distribution, it seems that they are "inside the range."

Fig. 7. Histogram of the PT_POOR variable.

This judgment is somewhat subjective. The empirical rule states that emissions must be taken into account if observation (or observations) does not fall into the interval (mean ± 3 multiplied by the standard deviation). In this case, it is necessary to repeat the analysis with emissions and without to make sure that they do not have a serious effect on the correlation between members of the aggregate.

Scattering diagram

If one of the hypotheses of a priori about the relationship between the specified variables, it is useful to check it on the graph of the corresponding scattering chart.

Fig. 8. Scattering diagram.

The scattering diagram shows an explicit negative correlation (-.65) between two variables. It also shows a 95% confidence interval for the regression line, i.e., with a 95% probability, the regression line passes between two dotted curves.

Criteria significance

Fig. 9. Table containing the criteria for significance.

The criterion for the POP_CHNG regression coefficient confirms that Pop_CHNG is strongly connected with PT_POOR, P<.001 .

Outcome

This example shows how to analyze a simple regression plan. The interpretation of non-standardized and standardized regression coefficients was also presented. The importance of studying the distribution of responses of the dependent variable was discussed, the technique of determining the direction and strength of the relationship between the predictor and the dependent variable was demonstrated.

During study, students are very often encountered with a variety of equations. One of them is the regression equation - considered in this article. This type of equation is used specifically to describe the characteristics of the relationship between mathematical parameters. This type of equalities are used in statistics and econometrics.

Definition of the concept of regression

In mathematics under regression, it is meant a certain amount describing the dependence of the average value of the set of data from the values \u200b\u200bof another value. The regression equation shows as a function of a certain feature the mean value of another feature. The regression function has a form of a simple equation y \u003d x, in which it acts as a dependent variable, and x - independent (sign factor). In fact, regression is expressed as y \u003d f (x).

What are the types of links between variables

In general, there are two opposite types of interconnection: correlation and regression.

The first is characterized by the equality of conditional variables. In this case, it is not reliably known which variable depends on the other.

If there is no equality between the variables and is not observed and in the conditions it is said, which variable explains, and which is dependent, then we can talk about the availability of the second type. In order to build a linear regression equation, it will be necessary to find out which type of communication is observed.

Types of regression

To date, 7 diverse types of regression are distinguished: hyperbolic, linear, multiple, nonlinear, steam room, reverse, logarithmically linear.

Hyperbolic, linear and logarithmic

The linear regression equation is used in statistics to clearly explain the parameters of the equation. It looks like y \u003d c + t * x + e. The hyperbolic equation has the form of the correct hyperbole y \u003d C + T / X + E. The logarithmically linear equation expresses the relationship with the help of a logarithmic function: in y \u003d in s + t * in x + in E.

Multiple and nonlinear

Two more complex types of regression are multiple and nonlinear. The multiple regression equation is expressed by the function y \u003d f (x 1, x 2 ... x C) + E. In this situation, it acts as a dependent variable, and x - explaining. The variable E is stochastic, it includes the influence of other factors in the equation. The nonlinear regression equation is slightly contradictory. On the one hand, with respect to the recorded indicators, it is not linear, and on the other hand, in the role of evaluation of indicators it is linear.

Reverse and Stery Types of Regression

Reverse is such a type of function that needs to be converted into a linear view. In the most traditional applied programs, it has the form of the function y \u003d 1 / s + t * x + e. The pair of regression equation demonstrates the relationship between the data as a function y \u003d f (x) + E. In the same way, as in other equations, it depends on x, and E is a stochastic parameter.

Concept of correlation

This is an indicator that demonstrates the existence of the relationship of two phenomena or processes. The relationship force is expressed as the correlation coefficient. Its value varies within the interval [-1; +1]. The negative indicator indicates about the presence of feedback, positive - about direct. If the coefficient takes a value equal to 0, then there is no relationship. The closer the value to 1 is the stronger the connection between the parameters, the closer to 0 - the weaker.

Methods

Correlation parametric methods can evaluate the relationship of the relationship. They are used on the basis of the distribution estimate to explore the parameters subject to the law of the normal distribution.

The parameters of the linear regression equation are necessary to identify the type of dependence, the functions of the regression equation and evaluating the indicators of the elected formula of the relationship. A correlation field is used as a communication identification method. To do this, all existing data must be depicted graphically. In a rectangular two-dimensional coordinate system, you must apply all known data. So the field of correlation is formed. The value of the describing factor is noted along the abscissa axis, while the values \u200b\u200bof the dependent - along the axis of the ordinate. If there is a functional dependence between the parameters, they are built in the form of a line.

If the correlation coefficient of such data is less than 30%, we can talk about the almost complete absence of communication. If it is between 30% and 70%, then this indicates the presence of connections of medium tightness. 100% indicator - evidence of functional communication.

The nonlinear regression equation is as long as the linear one, it is necessary to supplement the correlation index (R).

Correlation for multiple regression

The determination coefficient is an indicator of the square of the plural correlation. He talks about the closeness of the relationship of the presented complex of indicators with the studied sign. He can also talk about the nature of the effect of parameters on the result. The multiple regression equation is estimated by this indicator.

In order to calculate the indicator of the plural correlation, it is necessary to calculate its index.

Least square method

This method is a way of assessing regression factors. Its essence is to minimize the amount of deviations in the square obtained due to the dependence of the factor from the function.

The pair linear regression equation can be assessed using this method. This type of equations are used in case of detection between pair linear dependence indicators.

Parameters of equations

Each parameter of the linear regression function carries a certain meaning. The pair linear regression equation contains two parameters: C, etc. The parameter T demonstrates the average change in the final function of the function y, under the condition of decreasing (increase) of the variable x per intercourse. If the variable x is zero, the function is equal to the parameter with. If the variable x is not zero, then the factor C does not carry economic meaning. The only effect on the function has a sign before the factor with. If there is minus, then we can say about a slow change in the result compared to the factor. If there is plus, this indicates an accelerated change in the result.

Each parameter changing the value of the regression equation can be expressed through the equation. For example, the factor C has the form C \u003d Y - TX.

Grouped data

There are such conditions for the task in which all information is grouped by the X attribute, but at the same time the corresponding average values \u200b\u200bof the dependent indicator are indicated for a specific group. In this case, the average values \u200b\u200bare characterized by how the indicator is changed depending on x. Thus, the grouped information helps to find the regression equation. It is used as an analysis of relationships. However, this method has its drawbacks. Unfortunately, the average indicators are often exposed to external fluctuations. Data oscillations are not displaying patterns of relationships, they just mask it "noise". The average indicators demonstrate the patterns of relationships are much worse than the linear regression equation. However, they can be applied as a base for searching the equation. Multifying the number of a separate aggregate on the appropriate average can be obtained by the amount of in the group. Next, it is necessary to sink all the amounts received and find the final indicator. Easily harder to make calculations with the indicator of the amount of Hu. In that case, if the intervals are small, it is possible to conditionally take the x for all units (within the group) the same. It should multiply it with the amount of U to find out the amount of the works of X on y. Further, all amounts get together and the total amount of Hu is obtained.

Multiple pair of regression equation: Evaluation of the importance of communication

As previously was considered, the multiple regression has a function of the form y \u003d f (x 1, x 2, ..., x m) + e. Most often, such an equation is used to solve the problem of supply and supply for goods, interest income on redefined shares, studying the causes and type of production costs. It is also actively used in a wide variety of macroeconomic studies and calculations, but at the level of microeconomics such an equation is applied a little less.

The main task of multiple regression is to build a data model containing a huge amount of information in order to further determine what effect each of the factors are separate and in their total aggregate to the indicator that must be modeled and its coefficients. The regression equation can take a wide variety of values. At the same time, two types of functions are used to assess the relationship: linear and nonlinear.

The linear function is depicted in the form of such interconnection: y \u003d a 0 + a 1 x 1 + a 2 x 2, + ... + a m x m. At the same time A2, A M, are considered the coefficients of "clean" regression. They are necessary for the characteristics of the average parameter of the parameter y with a change (decrease in or increasing) of each corresponding parameter x per unit, with the condition of the stable value of other indicators.

Nonlinear equations have, for example, the type of power function y \u003d ah 1 b1 x 2 b2 ... x m bm. In this case, the indicators B 1, B 2 ..... b M are called elasticity coefficients, they demonstrate how the result will change (as%) with an increase in (decreasing) of the corresponding indicator of X by 1% and with a stable indicator of the remaining factors.

What factors need to be considered when building multiple regression

In order to properly build multiple regression, it is necessary to find out which factors should pay special attention to.

It is necessary to have a certain understanding of the nature of the relationship between economic factors and is modeled. The factors that will need to include are obliged to meet the following features:

• Must be subject to quantitative measurement. In order to use a factor describing the quality of the subject, in any case, it should be quantified.
• Intercorregulation of factors, or functional relationship. Such actions most often lead to irreversible consequences - the system of ordinary equations is not caused, and this entails its unreliability and non-accuracy of estimates.
• In the event of an existence of a huge indicator of the correlation, there is no way to determine the isolated influence of factors on the final result of the indicator, therefore, the coefficients become non-interpreted.

Construction methods

There is a huge number of methods and methods explaining how the factors can be selected for the equation. However, all these methods are built on the selection of coefficients using the correlation indicator. Among them are distinguished:

• Method of exception.
• Method of inclusion.
• Step-by-step regression analysis.

The first method implies the examinations of all coefficients from the total set. The second method includes the introduction of a plurality of additional factors. Well, the third - outliest factors that were previously applied to the equation. Each of these methods has the right to exist. They have their pros and cons, but they can all in their own way to solve the question of discraining unnecessary indicators. As a rule, the results obtained by each individual method are quite close.

Methods of multidimensional analysis

Such methods for determining factors are based on the consideration of individual combinations of interconnected signs. They include discriminant analysis, appearance recognition, the method of the main component and the analysis of clusters. In addition, there is also a factor analysis, however, it appeared due to the development of the component method. All of them are applied in certain circumstances, with certain conditions and factors.