पाइथागोरस प्रमेय क्या हैं? सही त्रिकोण

ज्यामिति कोई साधारण विज्ञान नहीं है। यह स्कूली पाठ्यक्रम और वास्तविक जीवन दोनों के लिए उपयोगी हो सकता है। कई सूत्रों और प्रमेयों का ज्ञान ज्यामितीय गणनाओं को सरल बना देगा। ज्यामिति की सबसे सरल आकृतियों में से एक त्रिभुज है। त्रिभुजों की किस्मों में से एक, समबाहु, की अपनी विशेषताएं हैं।

समबाहु त्रिभुज की विशेषताएँ

परिभाषा के अनुसार, त्रिभुज एक बहुफलक है जिसमें तीन कोण और तीन भुजाएँ होती हैं। यह एक सपाट द्वि-आयामी आकृति है, इसके गुणों का अध्ययन हाई स्कूल में किया जाता है। कोण के प्रकार के आधार पर न्यून, अधिक और समकोण त्रिभुज होते हैं। समकोण त्रिभुज एक ज्यामितीय आकृति है जिसका एक कोण 90º होता है। ऐसे त्रिभुज के दो पैर होते हैं (वे एक समकोण बनाते हैं) और एक कर्ण होता है (यह समकोण के विपरीत होता है)। ज्ञात मात्राओं के आधार पर, समकोण त्रिभुज के कर्ण की गणना करने के तीन सरल तरीके हैं।

पहला तरीका एक समकोण त्रिभुज का कर्ण ज्ञात करना है। पाइथागोरस प्रमेय

पाइथागोरस प्रमेय समकोण त्रिभुज की किसी भी भुजा की गणना करने का सबसे पुराना तरीका है। यह इस तरह लगता है: "एक समकोण त्रिभुज में, कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है।" इस प्रकार, कर्ण की गणना करने के लिए, किसी को दो पैरों के वर्ग के योग का वर्गमूल निकालना होगा। स्पष्टता के लिए, सूत्र और एक आरेख दिया गया है।

दूसरा तरीका. 2 ज्ञात मात्राओं का उपयोग करके कर्ण की गणना: पैर और आसन्न कोण

समकोण त्रिभुज के गुणों में से एक यह बताता है कि पैर की लंबाई और कर्ण की लंबाई का अनुपात इस पैर और कर्ण के बीच के कोण की कोज्या के बराबर है। आइए हम ज्ञात कोण को α कहते हैं। अब, प्रसिद्ध परिभाषा के लिए धन्यवाद, आप आसानी से कर्ण की गणना के लिए एक सूत्र तैयार कर सकते हैं: कर्ण = पैर/cos(α)

तीसरा तरीका. 2 ज्ञात मात्राओं का उपयोग करके कर्ण की गणना: पाद और विपरीत कोण

यदि विपरीत कोण ज्ञात है, तो समकोण त्रिभुज के गुणों का फिर से उपयोग करना संभव है। पैर की लंबाई और कर्ण का अनुपात विपरीत कोण की ज्या के बराबर होता है। आइए हम फिर से ज्ञात कोण को α कहते हैं। अब गणना के लिए हम थोड़ा अलग सूत्र का उपयोग करेंगे:
कर्ण = पैर/पाप (α)

सूत्रों को समझने में आपकी सहायता के लिए उदाहरण

प्रत्येक सूत्र की गहरी समझ के लिए, आपको उदाहरणात्मक उदाहरणों पर विचार करना चाहिए। तो, मान लीजिए कि आपको एक समकोण त्रिभुज दिया गया है, जहां निम्नलिखित डेटा है:

• पैर - 8 सेमी.
• आसन्न कोण cosα1 0.8 है।
• विपरीत कोण synα2 0.8 है।

पाइथागोरस प्रमेय के अनुसार: कर्ण = (36+64) का वर्गमूल = 10 सेमी।
पैर के आकार और आसन्न कोण के अनुसार: 8/0.8 = 10 सेमी.
पैर के आकार और विपरीत कोण के अनुसार: 8/0.8 = 10 सेमी.

एक बार जब आप सूत्र को समझ लेते हैं, तो आप किसी भी डेटा के साथ कर्ण की गणना आसानी से कर सकते हैं।

वीडियो: पाइथागोरस प्रमेय

(बर्लिन संग्रहालय के पपीरस 6619 के अनुसार)। कैंटर के अनुसार, हार्पेडोनैप्टेस, या "रस्सी खींचने वालों" ने 3, 4 और 5 भुजाओं वाले समकोण त्रिभुजों का उपयोग करके समकोण बनाया।

उनकी निर्माण पद्धति को पुन: प्रस्तुत करना बहुत आसान है। आइए 12 मीटर लंबी एक रस्सी लें और उसके एक सिरे से 3 मीटर और दूसरे सिरे से 4 मीटर की दूरी पर एक रंगीन पट्टी बांधें। समकोण 3 और 4 मीटर लंबी भुजाओं के बीच होगा। हार्पेडोनैप्टस पर इस बात पर आपत्ति की जा सकती है कि यदि कोई, उदाहरण के लिए, एक लकड़ी के वर्ग का उपयोग करता है, जिसका उपयोग सभी बढ़ई करते हैं, तो उनकी निर्माण पद्धति अनावश्यक हो जाती है। दरअसल, मिस्र के चित्र ज्ञात हैं जिनमें ऐसा उपकरण पाया जाता है, उदाहरण के लिए, बढ़ईगीरी कार्यशाला को दर्शाने वाले चित्र।

बेबीलोनियों के बीच पाइथागोरस प्रमेय के बारे में कुछ अधिक जानकारी है। एक पाठ में हम्मूराबी के समय का, यानी 2000 ईसा पूर्व का समय बताया गया है। ई. , एक समकोण त्रिभुज के कर्ण की अनुमानित गणना दी गई है। इससे हम यह निष्कर्ष निकाल सकते हैं कि मेसोपोटामिया में वे कम से कम कुछ मामलों में समकोण त्रिभुजों के साथ गणना करने में सक्षम थे। एक ओर, मिस्र और बेबीलोनियाई गणित के बारे में ज्ञान के वर्तमान स्तर के आधार पर, और दूसरी ओर, ग्रीक स्रोतों के एक महत्वपूर्ण अध्ययन के आधार पर, वान डेर वेर्डन (एक डच गणितज्ञ) ने निष्कर्ष निकाला कि इस बात की बहुत अधिक संभावना है कि कर्ण के वर्ग पर प्रमेय भारत में 18वीं शताब्दी ईसा पूर्व के आसपास ही ज्ञात था। ई.

लगभग 400 ई.पू. ईसा पूर्व, प्रोक्लस के अनुसार, प्लेटो ने बीजगणित और ज्यामिति को मिलाकर पायथागॉरियन त्रिक खोजने की एक विधि दी। लगभग 300 ई.पू. ई. पाइथागोरस प्रमेय का सबसे पुराना स्वयंसिद्ध प्रमाण यूक्लिड के तत्वों में दिखाई दिया।

योगों

ज्यामितीय सूत्रीकरण:

प्रमेय मूल रूप से इस प्रकार तैयार किया गया था:

बीजगणितीय सूत्रीकरण:

अर्थात्, त्रिभुज के कर्ण की लंबाई को , और पैरों की लंबाई को और द्वारा निरूपित करना:

प्रमेय के दोनों सूत्रीकरण समतुल्य हैं, लेकिन दूसरा सूत्रीकरण अधिक प्राथमिक है, इसमें क्षेत्रफल की अवधारणा की आवश्यकता नहीं है; अर्थात्, दूसरे कथन को क्षेत्रफल के बारे में कुछ भी जाने बिना और केवल एक समकोण त्रिभुज की भुजाओं की लंबाई मापकर सत्यापित किया जा सकता है।

व्युत्क्रम पाइथागोरस प्रमेय:

सबूत

पर इस समयइस प्रमेय के 367 प्रमाण वैज्ञानिक साहित्य में दर्ज किये गये हैं। संभवतः, पाइथागोरस प्रमेय इतनी प्रभावशाली संख्या में प्रमाणों वाला एकमात्र प्रमेय है। ऐसी विविधता को केवल ज्यामिति के लिए प्रमेय के मूलभूत महत्व द्वारा ही समझाया जा सकता है।

बेशक, वैचारिक रूप से उन सभी को कम संख्या में वर्गों में विभाजित किया जा सकता है। उनमें से सबसे प्रसिद्ध: क्षेत्र विधि द्वारा प्रमाण, स्वयंसिद्ध और विदेशी प्रमाण (उदाहरण के लिए, अंतर समीकरणों का उपयोग करके)।

समरूप त्रिभुजों के माध्यम से

बीजगणितीय सूत्रीकरण का निम्नलिखित प्रमाण, स्वयंसिद्धों से सीधे निर्मित, प्रमाणों में सबसे सरल है। विशेष रूप से, यह किसी आकृति के क्षेत्रफल की अवधारणा का उपयोग नहीं करता है।

होने देना एबीसीसमकोण वाला एक समकोण त्रिभुज है सी. आइए ऊंचाई खींचते हैं सीऔर इसके आधार को निरूपित करें एच. त्रिकोण आकएक त्रिकोण के समान एबीसीदो कोनों पर. इसी तरह, त्रिकोण सीबीएचसमान एबीसी. संकेतन का परिचय देकर

हम पाते हैं

समतुल्य क्या है

इसे जोड़ने पर हमें प्राप्त होता है

क्षेत्र विधि का उपयोग कर प्रमाण

नीचे दिए गए प्रमाण, अपनी स्पष्ट सरलता के बावजूद, बिल्कुल भी इतने सरल नहीं हैं। वे सभी क्षेत्रफल के गुणों का उपयोग करते हैं, जिसका प्रमाण पाइथागोरस प्रमेय के प्रमाण से भी अधिक जटिल है।

समसंपूरकता के माध्यम से प्रमाण

1. आइए चित्र 1 में दिखाए अनुसार चार समान समकोण त्रिभुजों की व्यवस्था करें।
2. भुजाओं वाला चतुर्भुज सीएक वर्ग है, क्योंकि दो न्यून कोणों का योग 90° होता है, और सीधा कोण 180° होता है।
3. संपूर्ण आकृति का क्षेत्रफल, एक ओर, भुजा (a + b) वाले एक वर्ग के क्षेत्रफल के बराबर है, और दूसरी ओर, चारों त्रिभुजों के क्षेत्रफलों के योग के बराबर है और भीतरी वर्ग का क्षेत्रफल.

क्यू.ई.डी.

यूक्लिड का प्रमाण

यूक्लिड के प्रमाण का विचार इस प्रकार है: आइए यह सिद्ध करने का प्रयास करें कि कर्ण पर बने वर्ग का आधा क्षेत्रफल पैरों पर बने वर्ग के आधे क्षेत्रफल के योग के बराबर है, और फिर के क्षेत्रफल के बराबर है बड़े और दो छोटे वर्ग बराबर हैं।

आइए बाईं ओर के चित्र को देखें। इस पर हमने एक समकोण त्रिभुज के किनारों पर वर्ग बनाए और समकोण C के शीर्ष से कर्ण AB के लंबवत एक किरण s खींची, यह कर्ण पर बने वर्ग ABIK को दो आयतों - BHJI और HAKJ में काटती है, क्रमश। इससे पता चलता है कि इन आयतों का क्षेत्रफल संबंधित पैरों पर बने वर्गों के क्षेत्रफल के बिल्कुल बराबर है।

आइए यह सिद्ध करने का प्रयास करें कि वर्ग DECA का क्षेत्रफल आयत AHJK के क्षेत्रफल के बराबर है। ऐसा करने के लिए, हम एक सहायक अवलोकन का उपयोग करेंगे: समान ऊँचाई और आधार वाले त्रिभुज का क्षेत्रफल दिया गया आयत दिए गए आयत के क्षेत्रफल के आधे के बराबर है। यह एक त्रिभुज के क्षेत्रफल को आधार और ऊँचाई के आधे गुणनफल के रूप में परिभाषित करने का परिणाम है। इस अवलोकन से यह निष्कर्ष निकलता है कि त्रिभुज ACK का क्षेत्रफल त्रिभुज AHK के क्षेत्रफल के बराबर है (आकृति में नहीं दिखाया गया है), जो बदले में आयत AHJK के क्षेत्रफल के आधे के बराबर है।

आइए अब सिद्ध करें कि त्रिभुज ACK का क्षेत्रफल भी वर्ग DECA के आधे क्षेत्रफल के बराबर है। इसके लिए केवल एक ही काम करना है वह है त्रिभुज ACK और BDA की समानता सिद्ध करना (चूँकि त्रिभुज BDA का क्षेत्रफल उपरोक्त संपत्ति के अनुसार वर्ग के आधे क्षेत्रफल के बराबर है)। यह समानता स्पष्ट है: त्रिभुजों की दोनों भुजाएँ और उनके बीच का कोण बराबर होता है। अर्थात् - AB=AK, AD=AC - कोण CAK और BAD की समानता को गति की विधि से सिद्ध करना आसान है: हम त्रिभुज CAK को 90° वामावर्त घुमाते हैं, तो यह स्पष्ट है कि दोनों त्रिभुजों की संगत भुजाएँ प्रश्न संपाती होगा (इस तथ्य के कारण कि वर्ग के शीर्ष पर कोण 90° है)।

वर्ग बीसीएफजी और आयत बीएचजीआई के क्षेत्रफलों की समानता का तर्क पूरी तरह समान है।

इस प्रकार, हमने सिद्ध किया कि कर्ण पर बने वर्ग का क्षेत्रफल पैरों पर बने वर्गों के क्षेत्रफल से बना होता है। इस प्रमाण के पीछे का विचार ऊपर दिए गए एनीमेशन द्वारा और भी स्पष्ट किया गया है।

लियोनार्डो दा विंची का प्रमाण

प्रमाण के मुख्य तत्व समरूपता और गति हैं।

आइए ड्राइंग पर विचार करें, जैसा कि समरूपता से देखा जा सकता है, खंड वर्ग को दो समान भागों में काटता है (क्योंकि त्रिकोण निर्माण में समान हैं)।

बिंदु के चारों ओर 90-डिग्री वामावर्त घुमाव का उपयोग करके, हम छायांकित आकृतियों की समानता देखते हैं।

अब यह स्पष्ट है कि जिस आकृति को हमने छायांकित किया है उसका क्षेत्रफल छोटे वर्गों (पैरों पर बने) के आधे क्षेत्रफल और मूल त्रिभुज के क्षेत्रफल के योग के बराबर है। दूसरी ओर, यह बड़े वर्ग (कर्ण पर निर्मित) के आधे क्षेत्रफल और मूल त्रिभुज के क्षेत्रफल के बराबर है। इस प्रकार, छोटे वर्गों के क्षेत्रफलों का आधा योग बड़े वर्ग के आधे क्षेत्रफल के बराबर होता है, और इसलिए पैरों पर बने वर्गों के क्षेत्रफलों का योग पैरों पर बने वर्गों के क्षेत्रफल के बराबर होता है कर्ण.

अनन्तिमल विधि से प्रमाण

विभेदक समीकरणों का उपयोग करते हुए निम्नलिखित प्रमाण का श्रेय अक्सर प्रसिद्ध अंग्रेजी गणितज्ञ हार्डी को दिया जाता है, जो 20वीं शताब्दी के पूर्वार्द्ध में रहते थे।

चित्र में दिखाए गए चित्र को देखें और पार्श्व में परिवर्तन का अवलोकन करें ए, हम अपरिमित पार्श्व वृद्धि के लिए निम्नलिखित संबंध लिख सकते हैं साथऔर ए(त्रिभुज समानता का उपयोग करके):

चरों को अलग करने की विधि का उपयोग करके, हम पाते हैं

दोनों तरफ वृद्धि के मामले में कर्ण में परिवर्तन के लिए एक अधिक सामान्य अभिव्यक्ति

इस समीकरण को एकीकृत करने और प्रारंभिक शर्तों का उपयोग करने पर, हम प्राप्त करते हैं

इस प्रकार हम वांछित उत्तर पर पहुँचते हैं

जैसा कि देखना आसान है, अंतिम सूत्र में द्विघात निर्भरता त्रिभुज की भुजाओं और वेतन वृद्धि के बीच रैखिक आनुपातिकता के कारण प्रकट होती है, जबकि योग विभिन्न पैरों की वृद्धि से स्वतंत्र योगदान से जुड़ा होता है।

एक सरल प्रमाण प्राप्त किया जा सकता है यदि हम मान लें कि पैरों में से एक में वृद्धि का अनुभव नहीं होता है (इस मामले में पैर)। फिर एकीकरण स्थिरांक के लिए हमें प्राप्त होता है

विविधताएं और सामान्यीकरण

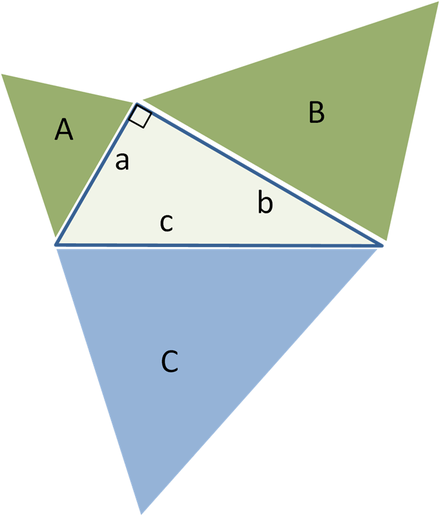
तीन तरफ समान ज्यामितीय आकृतियाँ

समरूप त्रिभुजों के लिए सामान्यीकरण, हरी आकृतियों का क्षेत्रफल A + B = नीले C का क्षेत्रफल

समान समकोण त्रिभुजों का उपयोग करते हुए पाइथागोरस प्रमेय

यूक्लिड ने अपने काम में पाइथागोरस प्रमेय का सामान्यीकरण किया शुरुआत, समान ज्यामितीय आकृतियों के किनारों पर वर्गों के क्षेत्रों का विस्तार करना:

यदि हम एक समकोण त्रिभुज की भुजाओं पर समान ज्यामितीय आकृतियाँ (यूक्लिडियन ज्यामिति देखें) बनाते हैं, तो दो छोटी आकृतियों का योग बड़ी आकृति के क्षेत्रफल के बराबर होगा।

इस सामान्यीकरण का मुख्य विचार यह है कि ऐसी ज्यामितीय आकृति का क्षेत्रफल उसके किसी भी रैखिक आयाम के वर्ग और विशेष रूप से, किसी भी भुजा की लंबाई के वर्ग के समानुपाती होता है। इसलिए, क्षेत्रफल वाले समान आंकड़ों के लिए ए, बीऔर सीलम्बाई के साथ किनारों पर निर्मित ए, बीऔर सी, हमारे पास है:

लेकिन, पाइथागोरस प्रमेय के अनुसार, ए 2 + बी 2 = सी 2 तो ए + बी = सी.

इसके विपरीत, यदि हम यह सिद्ध कर सकें ए + बी = सीपाइथागोरस प्रमेय का उपयोग किए बिना तीन समान ज्यामितीय आकृतियों के लिए, हम विपरीत दिशा में चलते हुए, प्रमेय को स्वयं सिद्ध कर सकते हैं। उदाहरण के लिए, प्रारंभिक केंद्र त्रिभुज को त्रिभुज के रूप में पुन: उपयोग किया जा सकता है सीकर्ण पर, और दो समान समकोण त्रिभुज ( एऔर बी), अन्य दो भुजाओं पर निर्मित, जो केंद्रीय त्रिभुज को उसकी ऊंचाई से विभाजित करके बनाई गई हैं। इस प्रकार, दो छोटे त्रिभुजों के क्षेत्रफलों का योग स्पष्ट रूप से तीसरे के क्षेत्रफल के बराबर होता है ए + बी = सीऔर, पिछले प्रमाण को उल्टे क्रम में निष्पादित करते हुए, हम पाइथागोरस प्रमेय a 2 + b 2 = c 2 प्राप्त करते हैं।

कोसाइन प्रमेय

पाइथागोरस प्रमेय अधिक सामान्य कोसाइन प्रमेय का एक विशेष मामला है, जो एक मनमाना त्रिभुज में भुजाओं की लंबाई से संबंधित है:

जहाँ θ भुजाओं के बीच का कोण है एऔर बी.

यदि θ 90 डिग्री है तो cos θ = 0 और सूत्र सामान्य पायथागॉरियन प्रमेय को सरल बनाता है।

मुक्त त्रिभुज

भुजाओं वाले एक मनमाना त्रिभुज के किसी चयनित कोने पर ए, बी, सीआइए हम एक समद्विबाहु त्रिभुज को इस प्रकार अंकित करें कि इसके आधार θ पर समान कोण चुने गए कोण के बराबर हों। आइए मान लें कि चयनित कोण θ निर्दिष्ट पक्ष के विपरीत स्थित है सी. परिणामस्वरूप, हमें कोण θ वाला त्रिभुज ABD प्राप्त हुआ, जो भुजा के विपरीत स्थित है एऔर पार्टियां आर. दूसरा त्रिभुज कोण θ से बनता है, जो भुजा के विपरीत स्थित है बीऔर पार्टियां साथलंबाई एसजैसा कि चित्र में दिखाया गया है। थाबित इब्न कुर्रा ने तर्क दिया कि इन तीन त्रिभुजों की भुजाएँ इस प्रकार संबंधित हैं:

जैसे-जैसे कोण θ π/2 के करीब पहुंचता है, समद्विबाहु त्रिभुज का आधार छोटा होता जाता है और दोनों भुजाएँ r और s एक-दूसरे को कम और कम ओवरलैप करते हैं। जब θ = π/2, ADB एक समकोण त्रिभुज बन जाता है, आर + एस = सीऔर हम प्रारंभिक पाइथागोरस प्रमेय प्राप्त करते हैं।

आइए एक तर्क पर विचार करें। त्रिभुज ABC के कोण त्रिभुज ABD के समान हैं, लेकिन विपरीत क्रम में। (दो त्रिभुजों के शीर्ष B पर एक उभयनिष्ठ कोण है, दोनों का एक कोण θ है और त्रिभुज के कोणों के योग के आधार पर तीसरा कोण भी समान है) तदनुसार, ABC त्रिभुज DBA के प्रतिबिंब ABD के समान है, क्योंकि निचले चित्र में दिखाया गया है। आइए हम सम्मुख भुजाओं और कोण θ के निकटवर्ती भुजाओं के बीच संबंध लिखें,

साथ ही एक अन्य त्रिभुज का प्रतिबिंब,

आइए भिन्नों को गुणा करें और इन दो अनुपातों को जोड़ें:

क्यू.ई.डी.

समांतर चतुर्भुज के माध्यम से मनमाना त्रिभुजों के लिए सामान्यीकरण

मनमाना त्रिभुजों के लिए सामान्यीकरण,
हरित क्षेत्र प्लॉट = क्षेत्रफलनीला

थीसिस का प्रमाण उपरोक्त चित्र में है

आइए वर्गों के बजाय तीन तरफ समांतर चतुर्भुज का उपयोग करके गैर-समकोण त्रिभुजों के लिए एक और सामान्यीकरण करें। (वर्ग एक विशेष मामला है।) शीर्ष आकृति से पता चलता है कि एक न्यून त्रिभुज के लिए, लंबी भुजा पर समांतर चतुर्भुज का क्षेत्रफल अन्य दो भुजाओं पर समांतर चतुर्भुज के योग के बराबर होता है, बशर्ते कि लंबी भुजा पर समांतर चतुर्भुज जैसा कि चित्र में दिखाया गया है, किनारे का निर्माण किया गया है (तीर द्वारा दर्शाए गए आयाम समान हैं और निचले समांतर चतुर्भुज के किनारों को निर्धारित करते हैं)। समांतर चतुर्भुज के साथ वर्गों का यह प्रतिस्थापन पाइथागोरस के प्रारंभिक प्रमेय से स्पष्ट समानता रखता है, माना जाता है कि इसे 4 ईस्वी में अलेक्जेंड्रिया के पप्पस द्वारा तैयार किया गया था। ई.

निचला आंकड़ा प्रमाण की प्रगति को दर्शाता है। आइए त्रिभुज के बाईं ओर देखें। बाएं हरे समांतर चतुर्भुज का क्षेत्रफल नीले समांतर चतुर्भुज के बाईं ओर के समान है क्योंकि उनका आधार समान है बीऔर ऊंचाई एच. इसके अतिरिक्त, बाएं हरे समांतर चतुर्भुज का क्षेत्रफल शीर्ष चित्र में बाएं हरे समांतर चतुर्भुज के समान है क्योंकि वे एक सामान्य आधार (त्रिभुज के शीर्ष बाईं ओर) और त्रिभुज के उस तरफ लंबवत एक सामान्य ऊंचाई साझा करते हैं। त्रिभुज की दाईं ओर के समान तर्क का उपयोग करते हुए, हम साबित करेंगे कि निचले समांतर चतुर्भुज का क्षेत्रफल दो हरे समांतर चतुर्भुजों के समान है।

जटिल संख्याएँ

पाइथागोरस प्रमेय का उपयोग कार्टेशियन समन्वय प्रणाली में दो बिंदुओं के बीच की दूरी खोजने के लिए किया जाता है, और यह प्रमेय सभी वास्तविक निर्देशांकों के लिए मान्य है: दूरी एसदो बिंदुओं के बीच ( ए, बी) और ( सी, डी) बराबर है

यदि सम्मिश्र संख्याओं को वास्तविक घटकों वाले सदिशों के रूप में माना जाए तो सूत्र में कोई समस्या नहीं है एक्स + मैं y = (एक्स, य). . उदाहरण के लिए, दूरी एस 0 + 1 के बीच मैंऔर 1 + 0 मैंवेक्टर के मापांक के रूप में गणना की गई (0, 1) − (1, 0) = (−1, 1), या

हालाँकि, जटिल निर्देशांक वाले वैक्टर के साथ संचालन के लिए, पाइथागोरस सूत्र में कुछ सुधार करना आवश्यक है। सम्मिश्र संख्याओं वाले बिंदुओं के बीच की दूरी ( ए, बी) और ( सी, डी); ए, बी, सी, और डीसभी जटिल, हम निरपेक्ष मानों का उपयोग करके तैयार करते हैं। दूरी एसवेक्टर अंतर के आधार पर (ए − सी, बी − डी) निम्नलिखित रूप में: अंतर बताएं ए − सी = पी+मैं क्यू, कहाँ पी- अंतर का वास्तविक हिस्सा, क्यूकाल्पनिक भाग है, और i = √(−1). वैसे ही चलो बी − डी = आर+मैं एस. तब:

के लिए सम्मिश्र संयुग्म संख्या कहाँ है? उदाहरण के लिए, बिंदुओं के बीच की दूरी (ए, बी) = (0, 1) और (सी, डी) = (मैं, 0) , आइए अंतर की गणना करें (ए − सी, बी − डी) = (−मैं, 1) और यदि जटिल संयुग्मों का उपयोग नहीं किया गया तो परिणाम 0 होगा। इसलिए, बेहतर सूत्र का उपयोग करके, हम प्राप्त करते हैं

मॉड्यूल को इस प्रकार परिभाषित किया गया है:

स्टीरियोमेट्री

त्रि-आयामी अंतरिक्ष के लिए पाइथागोरस प्रमेय का एक महत्वपूर्ण सामान्यीकरण डी गोय का प्रमेय है, जिसका नाम जे.-पी के नाम पर रखा गया है। डे गोइस: यदि एक चतुष्फलक में एक समकोण है (जैसे कि एक घन में), तो समकोण के विपरीत फलक के क्षेत्रफल का वर्ग अन्य तीन फलकों के क्षेत्रफलों के वर्गों के योग के बराबर होता है। इस निष्कर्ष को संक्षेप में प्रस्तुत किया जा सकता है " एन-आयामी पाइथागोरस प्रमेय":

त्रि-आयामी अंतरिक्ष में पाइथागोरस प्रमेय विकर्ण AD को तीन भुजाओं से जोड़ता है।

एक अन्य सामान्यीकरण: पाइथागोरस प्रमेय को निम्नलिखित रूप में स्टीरियोमेट्री पर लागू किया जा सकता है। चित्र में दिखाए अनुसार एक आयताकार समांतर चतुर्भुज पर विचार करें। आइए पाइथागोरस प्रमेय का उपयोग करके विकर्ण BD की लंबाई ज्ञात करें:

जहां तीन भुजाएं एक समकोण त्रिभुज बनाती हैं। हम विकर्ण AD की लंबाई ज्ञात करने के लिए क्षैतिज विकर्ण BD और ऊर्ध्वाधर किनारे AB का उपयोग करते हैं, इसके लिए हम फिर से पाइथागोरस प्रमेय का उपयोग करते हैं:

या, यदि हम सब कुछ एक समीकरण में लिखें:

यह परिणाम वेक्टर के परिमाण को निर्धारित करने के लिए एक त्रि-आयामी अभिव्यक्ति है वी(विकर्ण AD), इसके लंबवत घटकों के संदर्भ में व्यक्त किया गया ( वी k ) (तीन परस्पर लंबवत भुजाएँ):

इस समीकरण को बहुआयामी अंतरिक्ष के लिए पाइथागोरस प्रमेय के सामान्यीकरण के रूप में माना जा सकता है। हालाँकि, परिणाम वास्तव में पाइथागोरस प्रमेय को क्रमिक रूप से लंबवत विमानों में समकोण त्रिभुजों के अनुक्रम में बार-बार लागू करने से ज्यादा कुछ नहीं है।

सदिश स्थल

सदिशों की ऑर्थोगोनल प्रणाली के मामले में, एक समानता होती है, जिसे पाइथागोरस प्रमेय भी कहा जाता है:

यदि - ये समन्वय अक्षों पर वेक्टर के प्रक्षेपण हैं, तो यह सूत्र यूक्लिडियन दूरी के साथ मेल खाता है - और इसका मतलब है कि वेक्टर की लंबाई इसके घटकों के वर्गों के योग के वर्गमूल के बराबर है।

सदिशों की अनंत प्रणाली के मामले में इस समानता के अनुरूप को पार्सेवल की समानता कहा जाता है।

गैर-यूक्लिडियन ज्यामिति

पाइथागोरस प्रमेय यूक्लिडियन ज्यामिति के सिद्धांतों से लिया गया है और वास्तव में, गैर-यूक्लिडियन ज्यामिति के लिए उस रूप में मान्य नहीं है जिस रूप में यह ऊपर लिखा गया है। (अर्थात्, पाइथागोरस प्रमेय एक प्रकार से यूक्लिड के समांतरता के अभिधारणा के समतुल्य है) दूसरे शब्दों में, गैर-यूक्लिडियन ज्यामिति में एक त्रिभुज की भुजाओं के बीच का संबंध आवश्यक रूप से पाइथागोरस प्रमेय से भिन्न रूप में होगा। उदाहरण के लिए, गोलाकार ज्यामिति में, एक समकोण त्रिभुज की तीनों भुजाएँ (मान लीजिए ए, बीऔर सी), जो इकाई गोले के अष्टक (आठवें भाग) को सीमित करता है, उसकी लंबाई π/2 है, जो पाइथागोरस प्रमेय का खंडन करता है, क्योंकि ए 2 + बी 2 ≠ सी 2 .

आइए यहां गैर-यूक्लिडियन ज्यामिति के दो मामलों पर विचार करें - गोलाकार और अतिशयोक्तिपूर्ण ज्यामिति; दोनों मामलों में, समकोण त्रिभुजों के लिए यूक्लिडियन स्थान के लिए, परिणाम, जो पाइथागोरस प्रमेय को प्रतिस्थापित करता है, कोसाइन प्रमेय से होता है।

हालाँकि, पाइथागोरस प्रमेय हाइपरबोलिक और अण्डाकार ज्यामिति के लिए मान्य रहता है यदि आवश्यकता है कि त्रिभुज आयताकार है, इस शर्त से प्रतिस्थापित किया जाता है कि त्रिभुज के दो कोणों का योग तीसरे के बराबर होना चाहिए, मान लीजिए ए+बी = सी. तब भुजाओं के बीच का संबंध इस प्रकार दिखता है: व्यास वाले वृत्तों के क्षेत्रफलों का योग एऔर बीव्यास वाले वृत्त के क्षेत्रफल के बराबर सी.

गोलाकार ज्यामिति

त्रिज्या वाले गोले पर किसी समकोण त्रिभुज के लिए आर(उदाहरण के लिए, यदि किसी त्रिभुज में कोण γ समकोण है) भुजाओं के साथ ए, बी, सीपार्टियों के बीच संबंध इस तरह दिखेंगे:

इस समानता को गोलाकार कोसाइन प्रमेय के एक विशेष मामले के रूप में प्राप्त किया जा सकता है, जो सभी गोलाकार त्रिकोणों के लिए मान्य है:

जहां cosh हाइपरबोलिक कोसाइन है। यह सूत्र हाइपरबोलिक कोसाइन प्रमेय का एक विशेष मामला है, जो सभी त्रिकोणों के लिए मान्य है:

जहां γ वह कोण है जिसका शीर्ष भुजा के विपरीत है सी.

कहाँ जी आईजेमीट्रिक टेंसर कहा जाता है। यह पद का कार्य हो सकता है. ऐसे घुमावदार स्थानों में सामान्य उदाहरण के रूप में रीमानियन ज्यामिति शामिल है। वक्ररेखीय निर्देशांक का उपयोग करते समय यह सूत्रीकरण यूक्लिडियन अंतरिक्ष के लिए भी उपयुक्त है। उदाहरण के लिए, ध्रुवीय निर्देशांक के लिए:

वेक्टर कलाकृति

पाइथागोरस प्रमेय एक वेक्टर उत्पाद के परिमाण के लिए दो अभिव्यक्तियों को जोड़ता है। एक क्रॉस उत्पाद को परिभाषित करने के लिए एक दृष्टिकोण के लिए आवश्यक है कि यह समीकरण को संतुष्ट करे:

यह सूत्र डॉट उत्पाद का उपयोग करता है। समीकरण के दाएँ पक्ष को ग्राम निर्धारक कहा जाता है एऔर बी, जो इन दोनों सदिशों से बने समांतर चतुर्भुज के क्षेत्रफल के बराबर है। इस आवश्यकता के आधार पर, साथ ही यह आवश्यकता कि वेक्टर उत्पाद अपने घटकों के लंबवत हो एऔर बीइससे यह निष्कर्ष निकलता है कि, 0- और 1-आयामी स्थान से तुच्छ मामलों को छोड़कर, क्रॉस उत्पाद को केवल तीन और सात आयामों में परिभाषित किया गया है। हम कोण की परिभाषा का उपयोग करते हैं एन-आयामी स्थान:

किसी क्रॉस उत्पाद का यह गुण उसका परिमाण इस प्रकार बताता है:

पाइथागोरस की मौलिक त्रिकोणमितीय पहचान के माध्यम से हमें इसका मान लिखने का एक और रूप प्राप्त होता है:

किसी क्रॉस उत्पाद को परिभाषित करने का एक वैकल्पिक तरीका इसके परिमाण के लिए एक अभिव्यक्ति का उपयोग करना है। फिर, विपरीत क्रम में तर्क करते हुए, हम अदिश गुणनफल के साथ एक संबंध प्राप्त करते हैं:

यह भी देखें

टिप्पणियाँ

1. इतिहास विषय: बेबीलोनियाई गणित में पाइथागोरस का प्रमेय
2. ( , पृ. 351) पृ. 351
3. ( , खंड I, पृष्ठ 144)
4. (, पृ. 351) पृ. 351 में ऐतिहासिक तथ्यों की चर्चा दी गयी है
5. कर्ट वॉन फ्रिट्ज़ (अप्रैल, 1945)। "मेटापोंटम के हिप्पासस द्वारा असंगतता की खोज"। गणित के इतिहास, दूसरी श्रृंखला(गणित के इतिहास) 46 (2): 242–264.
6. लुईस कैरोल, "द स्टोरी विद नॉट्स", एम., मीर, 1985, पृ. 7
7. असगर आबोगणित के प्रारंभिक इतिहास के प्रसंग। - मैथमैटिकल एसोसिएशन ऑफ अमेरिका, 1997. - पी. 51. - आईएसबीएन 0883856131
8. पायथन प्रस्तावएलीशा स्कॉट लूमिस द्वारा
9. यूक्लिड का तत्वों: पुस्तक VI, प्रस्ताव VI 31: "समकोण त्रिभुजों में समकोण को अंतरित करने वाली भुजा पर बनी आकृति समकोण वाली भुजा पर समान और समान रूप से वर्णित आकृतियों के बराबर होती है।"
10. लॉरेंस एस लेफ़ उद्धृत कार्य. - बैरोन की शैक्षिक श्रृंखला - पी. 326. - आईएसबीएन 0764128922
11. हावर्ड व्हिटली ईव्स§4.8:...पाइथागोरस प्रमेय का सामान्यीकरण // गणित में महान क्षण (1650 से पहले)। - मैथमैटिकल एसोसिएशन ऑफ अमेरिका, 1983. - पी. 41. - आईएसबीएन 0883853108
12. ताबित इब्न क़ोरा (पूरा नाम थाबित इब्न क़ुर्रा इब्न मारवान अल-सबी अल-अर्रानी) (826-901 ईस्वी) बगदाद में रहने वाले एक चिकित्सक थे जिन्होंने यूक्लिड के तत्वों और अन्य गणितीय विषयों पर विस्तार से लिखा था।
13. आयदीन सायिली (मार्च 1960)। "थाबिट इब्न कुर्रा" का पाइथागोरस प्रमेय का सामान्यीकरण। आइसिस 51 (1): 35-37. डीओआई:10.1086/348837।
14. जूडिथ डी. सैली, पॉल सैलीअभ्यास 2.10 (ii) // उद्धृत कार्य। - पी. 62. - आईएसबीएन 0821844032
15. ऐसे निर्माण के विवरण के लिए देखें जॉर्ज जेनिंग्सचित्र 1.32: सामान्यीकृत पायथागॉरियन प्रमेय // अनुप्रयोगों के साथ आधुनिक ज्यामिति: 150 अंकों के साथ। - तीसरा. - स्प्रिंगर, 1997. - पी. 23. - आईएसबीएन 038794222एक्स
16. अर्लेन ब्राउन, कार्ल एम. पियर्सीवस्तु सी: मनमाना के लिए आदर्श एन-टुपल... // विश्लेषण का परिचय। - स्प्रिंगर, 1995. - पी. 124. - आईएसबीएन 0387943692पृष्ठ 47-50 भी देखें।
17. अल्फ्रेड ग्रे, एल्सा अब्बेना, साइमन सलामोनगणित के साथ वक्रों और सतहों की आधुनिक विभेदक ज्यामिति। - तीसरा. - सीआरसी प्रेस, 2006. - पी. 194. - आईएसबीएन 1584884487
18. राजेंद्र भाटियामैट्रिक्स विश्लेषण. - स्प्रिंगर, 1997. - पी. 21. - आईएसबीएन 0387948465
19. स्टीफन डब्ल्यू हॉकिंग उद्धृत कार्य. - 2005. - पी. 4. - आईएसबीएन 0762419229
20. एरिक डब्ल्यू वीसस्टीनसीआरसी गणित का संक्षिप्त विश्वकोश। - दूसरा. - 2003. - पी. 2147. - आईएसबीएन 1584883472
21. अलेक्जेंडर आर प्रुस

पाइथागोरस प्रमेय: पैरों पर स्थित वर्गों के क्षेत्रफलों का योग ( एऔर बी), कर्ण पर बने वर्ग के क्षेत्रफल के बराबर ( सी).

ज्यामितीय सूत्रीकरण:

प्रमेय मूल रूप से इस प्रकार तैयार किया गया था:

बीजगणितीय सूत्रीकरण:

अर्थात् त्रिभुज के कर्ण की लंबाई को इससे निरूपित करना सी, और पैरों की लंबाई के माध्यम से एऔर बी :

प्रमेय के दोनों सूत्रीकरण समतुल्य हैं, लेकिन दूसरा सूत्रीकरण अधिक प्राथमिक है, इसमें क्षेत्रफल की अवधारणा की आवश्यकता नहीं है; अर्थात्, दूसरे कथन को क्षेत्रफल के बारे में कुछ भी जाने बिना और केवल एक समकोण त्रिभुज की भुजाओं की लंबाई मापकर सत्यापित किया जा सकता है।

व्युत्क्रम पाइथागोरस प्रमेय:

सबूत

फिलहाल, इस प्रमेय के 367 प्रमाण वैज्ञानिक साहित्य में दर्ज किए गए हैं। संभवतः, पाइथागोरस प्रमेय इतनी प्रभावशाली संख्या में प्रमाणों वाला एकमात्र प्रमेय है। ऐसी विविधता को केवल ज्यामिति के लिए प्रमेय के मूलभूत महत्व द्वारा ही समझाया जा सकता है।

बेशक, वैचारिक रूप से उन सभी को कम संख्या में वर्गों में विभाजित किया जा सकता है। उनमें से सबसे प्रसिद्ध: क्षेत्रों की विधि द्वारा प्रमाण, स्वयंसिद्ध और विदेशी प्रमाण (उदाहरण के लिए, अंतर समीकरणों का उपयोग करके)।

समरूप त्रिभुजों के माध्यम से

बीजगणितीय सूत्रीकरण का निम्नलिखित प्रमाण, स्वयंसिद्धों से सीधे निर्मित, प्रमाणों में सबसे सरल है। विशेष रूप से, यह किसी आकृति के क्षेत्रफल की अवधारणा का उपयोग नहीं करता है।

होने देना एबीसीसमकोण वाला एक समकोण त्रिभुज है सी. आइए ऊंचाई खींचते हैं सीऔर इसके आधार को निरूपित करें एच. त्रिकोण आकएक त्रिकोण के समान एबीसीदो कोनों पर. इसी तरह, त्रिकोण सीबीएचसमान एबीसी. संकेतन का परिचय देकर

हम पाते हैं

समतुल्य क्या है

इसे जोड़ने पर हमें प्राप्त होता है

क्षेत्र विधि का उपयोग कर प्रमाण

नीचे दिए गए प्रमाण, अपनी स्पष्ट सरलता के बावजूद, बिल्कुल भी इतने सरल नहीं हैं। वे सभी क्षेत्रफल के गुणों का उपयोग करते हैं, जिसका प्रमाण पाइथागोरस प्रमेय के प्रमाण से भी अधिक जटिल है।

समसंपूरकता के माध्यम से प्रमाण

1. आइए चित्र 1 में दिखाए अनुसार चार समान समकोण त्रिभुजों की व्यवस्था करें।
2. भुजाओं वाला चतुर्भुज सीएक वर्ग है, क्योंकि दो न्यून कोणों का योग 90° होता है, और सीधा कोण 180° होता है।
3. संपूर्ण आकृति का क्षेत्रफल, एक ओर, भुजा (a + b) वाले एक वर्ग के क्षेत्रफल के बराबर है, और दूसरी ओर, चार त्रिभुजों और दो आंतरिक के क्षेत्रफलों के योग के बराबर है वर्ग.

क्यू.ई.डी.

तुल्यता के माध्यम से प्रमाण

क्रमपरिवर्तन का उपयोग करके सुंदर प्रमाण

ऐसे ही एक प्रमाण का उदाहरण दाईं ओर के चित्र में दिखाया गया है, जहां कर्ण पर बने एक वर्ग को पैरों पर बने दो वर्गों में पुनर्व्यवस्थित किया गया है।

यूक्लिड का प्रमाण

यूक्लिड के प्रमाण के लिए चित्रण

यूक्लिड के प्रमाण के लिए चित्रण

यूक्लिड के प्रमाण का विचार इस प्रकार है: आइए यह सिद्ध करने का प्रयास करें कि कर्ण पर बने वर्ग का आधा क्षेत्रफल पैरों पर बने वर्ग के आधे क्षेत्रफल के योग के बराबर है, और फिर के क्षेत्रफल के बराबर है बड़े और दो छोटे वर्ग बराबर हैं।

आइए बाईं ओर के चित्र को देखें। इस पर हमने एक समकोण त्रिभुज के किनारों पर वर्ग बनाए और समकोण C के शीर्ष से कर्ण AB के लंबवत एक किरण s खींची, यह कर्ण पर बने वर्ग ABIK को दो आयतों - BHJI और HAKJ में काटती है, क्रमश। इससे पता चलता है कि इन आयतों का क्षेत्रफल संबंधित पैरों पर बने वर्गों के क्षेत्रफल के बिल्कुल बराबर है।

आइए यह सिद्ध करने का प्रयास करें कि वर्ग DECA का क्षेत्रफल आयत AHJK के क्षेत्रफल के बराबर है। ऐसा करने के लिए, हम एक सहायक अवलोकन का उपयोग करेंगे: समान ऊँचाई और आधार वाले त्रिभुज का क्षेत्रफल दिया गया आयत दिए गए आयत के क्षेत्रफल के आधे के बराबर है। यह एक त्रिभुज के क्षेत्रफल को आधार और ऊँचाई के आधे गुणनफल के रूप में परिभाषित करने का परिणाम है। इस अवलोकन से यह निष्कर्ष निकलता है कि त्रिभुज ACK का क्षेत्रफल त्रिभुज AHK के क्षेत्रफल के बराबर है (आकृति में नहीं दिखाया गया है), जो बदले में आयत AHJK के क्षेत्रफल के आधे के बराबर है।

आइए अब सिद्ध करें कि त्रिभुज ACK का क्षेत्रफल भी वर्ग DECA के आधे क्षेत्रफल के बराबर है। इसके लिए केवल एक ही काम करना है वह है त्रिभुज ACK और BDA की समानता सिद्ध करना (चूँकि त्रिभुज BDA का क्षेत्रफल उपरोक्त संपत्ति के अनुसार वर्ग के आधे क्षेत्रफल के बराबर है)। समानता स्पष्ट है, त्रिभुजों की दोनों भुजाएँ और उनके बीच का कोण समान है। अर्थात् - AB=AK,AD=AC - कोण CAK और BAD की समानता को गति की विधि से सिद्ध करना आसान है: हम त्रिभुज CAK को 90° वामावर्त घुमाते हैं, तो यह स्पष्ट है कि दोनों त्रिभुजों की संगत भुजाएँ प्रश्न संपाती होगा (इस तथ्य के कारण कि वर्ग के शीर्ष पर कोण 90° है)।

वर्ग बीसीएफजी और आयत बीएचजीआई के क्षेत्रफलों की समानता का तर्क पूरी तरह समान है।

इस प्रकार, हमने सिद्ध किया कि कर्ण पर बने वर्ग का क्षेत्रफल पैरों पर बने वर्गों के क्षेत्रफल से बना होता है। इस प्रमाण के पीछे का विचार ऊपर दिए गए एनीमेशन द्वारा और भी स्पष्ट किया गया है।

लियोनार्डो दा विंची का प्रमाण

लियोनार्डो दा विंची का प्रमाण

प्रमाण के मुख्य तत्व समरूपता और गति हैं।

आइए ड्राइंग पर विचार करें, जैसा कि समरूपता से देखा जा सकता है, एक खंड सीमैंवर्ग काटता है एबीएचजे दो समान भागों में (त्रिभुज के बाद से)। एबीसीऔर जेएचमैंनिर्माण में बराबर)। 90 डिग्री वामावर्त घुमाव का उपयोग करके, हम छायांकित आकृतियों की समानता देखते हैं सीएजेमैं और जीडीएबी . अब यह स्पष्ट है कि जिस आकृति को हमने छायांकित किया है उसका क्षेत्रफल पैरों पर बने वर्गों के आधे क्षेत्रफल और मूल त्रिभुज के क्षेत्रफल के योग के बराबर है। दूसरी ओर, यह कर्ण पर बने वर्ग के आधे क्षेत्रफल और मूल त्रिभुज के क्षेत्रफल के बराबर है। प्रमाण का अंतिम चरण पाठक पर छोड़ दिया गया है।

अनन्तिमल विधि से प्रमाण

विभेदक समीकरणों का उपयोग करते हुए निम्नलिखित प्रमाण का श्रेय अक्सर प्रसिद्ध अंग्रेजी गणितज्ञ हार्डी को दिया जाता है, जो 20वीं शताब्दी के पूर्वार्द्ध में रहते थे।

चित्र में दिखाए गए चित्र को देखें और पार्श्व में परिवर्तन का अवलोकन करें ए, हम अपरिमित पार्श्व वृद्धि के लिए निम्नलिखित संबंध लिख सकते हैं साथऔर ए(त्रिभुज समानता का उपयोग करके):

अनन्तिमल विधि से प्रमाण

चरों को अलग करने की विधि का उपयोग करके, हम पाते हैं

दोनों तरफ वृद्धि के मामले में कर्ण में परिवर्तन के लिए एक अधिक सामान्य अभिव्यक्ति

इस समीकरण को एकीकृत करने और प्रारंभिक शर्तों का उपयोग करने पर, हम प्राप्त करते हैं

इस प्रकार हम वांछित उत्तर पर पहुँचते हैं

जैसा कि देखना आसान है, अंतिम सूत्र में द्विघात निर्भरता त्रिभुज की भुजाओं और वेतन वृद्धि के बीच रैखिक आनुपातिकता के कारण प्रकट होती है, जबकि योग विभिन्न पैरों की वृद्धि से स्वतंत्र योगदान से जुड़ा होता है।

एक सरल प्रमाण प्राप्त किया जा सकता है यदि हम मान लें कि पैरों में से एक में वृद्धि का अनुभव नहीं होता है (इस मामले में, पैर बी). फिर एकीकरण स्थिरांक के लिए हमें प्राप्त होता है

विविधताएं और सामान्यीकरण

• यदि हम वर्गों के बजाय किनारों पर अन्य समान आकृतियाँ बनाते हैं, तो पाइथागोरस प्रमेय का निम्नलिखित सामान्यीकरण सत्य है: एक समकोण त्रिभुज में, भुजाओं पर बनी समान आकृतियों के क्षेत्रफलों का योग कर्ण पर बनी आकृति के क्षेत्रफल के बराबर होता है।विशेष रूप से:
  • पैरों पर बने नियमित त्रिभुजों के क्षेत्रफल का योग कर्ण पर बने नियमित त्रिभुज के क्षेत्रफल के बराबर होता है।
  • पैरों पर बने अर्धवृत्त के क्षेत्रफलों का योग (व्यास के अनुसार) कर्ण पर बने अर्धवृत्त के क्षेत्रफल के बराबर होता है। इस उदाहरण का उपयोग दो वृत्तों के चापों से घिरी आकृतियों के गुणों को सिद्ध करने के लिए किया जाता है और जिन्हें हिप्पोक्रेटिक लुनुला कहा जाता है।

कहानी

चू-पेई 500-200 ई.पू. बाईं ओर शिलालेख है: ऊंचाई और आधार की लंबाई के वर्गों का योग कर्ण की लंबाई का वर्ग है।

प्राचीन चीनी पुस्तक चू-पेई 3, 4 और 5 भुजाओं वाले पाइथागोरस त्रिभुज के बारे में बात करती है: वही पुस्तक एक चित्र प्रस्तुत करती है जो बशारा के हिंदू ज्यामिति के चित्रों में से एक से मेल खाता है।

कैंटर (गणित के महानतम जर्मन इतिहासकार) का मानना ​​है कि समानता 3² + 4² = 5² मिस्रवासियों को 2300 ईसा पूर्व के आसपास पहले से ही ज्ञात थी। ई., राजा अमेनेमहट प्रथम के समय में (बर्लिन संग्रहालय के पपीरस 6619 के अनुसार)। कैंटर के अनुसार, हार्पेडोनैप्टेस, या "रस्सी खींचने वालों" ने 3, 4 और 5 भुजाओं वाले समकोण त्रिभुजों का उपयोग करके समकोण बनाया।

उनकी निर्माण पद्धति को पुन: प्रस्तुत करना बहुत आसान है। आइए 12 मीटर लंबी एक रस्सी लें और उसमें 3 मीटर की दूरी पर एक रंगीन पट्टी बांधें। एक छोर से और दूसरे छोर से 4 मीटर की दूरी पर। समकोण 3 और 4 मीटर लंबी भुजाओं के बीच घिरा होगा। हार्पेडोनैप्टियंस को इस बात पर आपत्ति हो सकती है कि यदि कोई, उदाहरण के लिए, एक लकड़ी के वर्ग का उपयोग करता है, जिसका उपयोग सभी बढ़ई द्वारा किया जाता है, तो निर्माण की उनकी पद्धति अनावश्यक हो जाती है। दरअसल, मिस्र के ऐसे चित्र ज्ञात हैं जिनमें ऐसा उपकरण पाया जाता है, उदाहरण के लिए, बढ़ई की कार्यशाला को दर्शाने वाले चित्र।

बेबीलोनियों के बीच पाइथागोरस प्रमेय के बारे में कुछ अधिक जानकारी है। एक पाठ में हम्मूराबी के समय का, यानी 2000 ईसा पूर्व का समय बताया गया है। ई., एक समकोण त्रिभुज के कर्ण की अनुमानित गणना दी गई है। इससे हम यह निष्कर्ष निकाल सकते हैं कि मेसोपोटामिया में वे कम से कम कुछ मामलों में समकोण त्रिभुजों के साथ गणना करने में सक्षम थे। एक ओर, मिस्र और बेबीलोनियाई गणित के बारे में ज्ञान के वर्तमान स्तर के आधार पर, और दूसरी ओर, ग्रीक स्रोतों के एक महत्वपूर्ण अध्ययन के आधार पर, वान डेर वेर्डन (डच गणितज्ञ) निम्नलिखित निष्कर्ष पर पहुंचे:

साहित्य

रूसी में

• स्कोपेट्स जेड. ए.ज्यामितीय लघुचित्र. एम., 1990
• एलेंस्की शच.पाइथागोरस के नक्शेकदम पर. एम., 1961
• वैन डेर वेर्डन बी.एल.जागृति विज्ञान. प्राचीन मिस्र, बेबीलोन और ग्रीस का गणित। एम., 1959
• ग्लेज़र जी.आई.स्कूल में गणित का इतिहास. एम., 1982
• डब्ल्यू. लित्ज़मैन, "पाइथागोरस प्रमेय" एम., 1960।
  • बड़ी संख्या में प्रमाणों के साथ पाइथागोरस प्रमेय के बारे में एक साइट, वी. लित्ज़मैन की पुस्तक से ली गई सामग्री, बड़ी संख्या में चित्र अलग-अलग ग्राफिक फ़ाइलों के रूप में प्रस्तुत किए गए हैं।
• पाइथागोरस प्रमेय और पाइथागोरस त्रिगुण अध्याय डी. वी. एनोसोव की पुस्तक "गणित पर एक नज़र और उससे कुछ" से
• पाइथागोरस प्रमेय और इसे साबित करने के तरीकों के बारे में जी. ग्लेसर, रूसी शिक्षा अकादमी, मॉस्को के शिक्षाविद

अंग्रेजी में

• वुल्फराममैथवर्ल्ड में पाइथागोरस प्रमेय
• कट-द-नॉट, पाइथागोरस प्रमेय पर अनुभाग, लगभग 70 प्रमाण और व्यापक अतिरिक्त जानकारी (अंग्रेजी)

विकिमीडिया फाउंडेशन.

2010.

पाइथागोरस प्रमेय ज्यामिति का सबसे महत्वपूर्ण कथन है। प्रमेय इस प्रकार तैयार किया गया है: एक समकोण त्रिभुज के कर्ण पर बने वर्ग का क्षेत्रफल उसके पैरों पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है।

इस कथन की खोज का श्रेय आमतौर पर प्राचीन यूनानी दार्शनिक और गणितज्ञ पाइथागोरस (छठी शताब्दी ईसा पूर्व) को दिया जाता है। लेकिन बेबीलोनियाई क्यूनिफॉर्म गोलियों और प्राचीन चीनी पांडुलिपियों (यहां तक ​​कि पुरानी पांडुलिपियों की प्रतियां) के अध्ययन से पता चला कि यह कथन पाइथागोरस से बहुत पहले से जाना जाता था, शायद उससे एक सहस्राब्दी पहले। पाइथागोरस की योग्यता यह थी कि उन्होंने इस प्रमेय का प्रमाण खोज निकाला।

हालाँकि, दो हजार वर्षों तक, यह दृश्य प्रमाण नहीं था जिसका उपयोग किया गया था, बल्कि यूक्लिड द्वारा आविष्कार किया गया एक अधिक जटिल प्रमाण था, जिसे उनकी प्रसिद्ध पुस्तक "एलिमेंट्स" (यूक्लिड और उनके "एलिमेंट्स" देखें) में रखा गया है, यूक्लिड ने ऊंचाई कम कर दी समकोण के शीर्ष से कर्ण तक और सिद्ध किया गया है कि इसकी निरंतरता कर्ण पर बने वर्ग को दो आयतों में विभाजित करती है, जिनका क्षेत्रफल पैरों पर बने संगत वर्गों के क्षेत्रफल के बराबर होता है (चित्र 3)। इस प्रमेय को सिद्ध करने के लिए उपयोग किए गए चित्र को मजाक में "पायथागॉरियन पैंट" कहा जाता है। लंबे समय तक इसे गणितीय विज्ञान के प्रतीकों में से एक माना जाता था।

आज, पाइथागोरस प्रमेय के कई दर्जन विभिन्न प्रमाण ज्ञात हैं। उनमें से कुछ वर्गों के विभाजन पर आधारित हैं, जिसमें कर्ण पर बने वर्ग में पैरों पर बने वर्गों के विभाजन में शामिल भाग शामिल होते हैं; अन्य - समान आंकड़ों के पूरक पर; तीसरा - इस तथ्य पर कि समकोण के शीर्ष से कर्ण तक की ऊंचाई एक समकोण त्रिभुज को उसके समान दो त्रिभुजों में विभाजित करती है।

पाइथागोरस प्रमेय अधिकांश ज्यामितीय गणनाओं का आधार है। प्राचीन बेबीलोन में भी, इसका उपयोग आधार और भुजा की लंबाई से एक समद्विबाहु त्रिभुज की ऊंचाई की गणना करने के लिए किया जाता था, वृत्त के व्यास और जीवा की लंबाई से एक खंड के तीर की गणना की जाती थी, और संबंध स्थापित किए जाते थे। कुछ नियमित बहुभुजों के तत्वों के बीच। पाइथागोरस प्रमेय का उपयोग करते हुए, हम इसके सामान्यीकरण को साबित करते हैं, जो हमें न्यून या अधिक कोण के विपरीत स्थित पक्ष की लंबाई की गणना करने की अनुमति देता है:

इस सामान्यीकरण से यह निष्कर्ष निकलता है कि समकोण की उपस्थिति न केवल पर्याप्त है, बल्कि समानता की संतुष्टि के लिए एक आवश्यक शर्त भी है। सूत्र (1) से संबंध इस प्रकार है एक समांतर चतुर्भुज के विकर्णों और भुजाओं की लंबाई के बीच, जिसकी सहायता से किसी त्रिभुज की भुजाओं की लंबाई से उसकी माध्यिका की लंबाई ज्ञात करना आसान होता है।

पाइथागोरस प्रमेय के आधार पर, एक सूत्र निकाला जाता है जो किसी भी त्रिभुज के क्षेत्रफल को उसकी भुजाओं की लंबाई के माध्यम से व्यक्त करता है (हेरॉन का सूत्र देखें)। बेशक, पाइथागोरस प्रमेय का उपयोग विभिन्न व्यावहारिक समस्याओं को हल करने के लिए भी किया गया था।

वर्गों के बजाय, आप समकोण त्रिभुज की भुजाओं पर कोई भी समान आकृतियाँ (समबाहु त्रिभुज, अर्धवृत्त, आदि) बना सकते हैं। इस स्थिति में कर्ण पर बनी आकृति का क्षेत्रफल पैरों पर बनी आकृति के क्षेत्रफल के योग के बराबर होता है। एक अन्य सामान्यीकरण समतल से अंतरिक्ष में संक्रमण से जुड़ा है। इसे निम्नानुसार तैयार किया गया है: एक आयताकार समांतर चतुर्भुज के विकर्ण लंबाई का वर्ग इसके आयामों (लंबाई, चौड़ाई और ऊंचाई) के वर्गों के योग के बराबर है। एक समान प्रमेय बहुआयामी और यहां तक ​​कि अनंत-आयामी मामलों में भी सत्य है।

पाइथागोरस प्रमेय केवल यूक्लिडियन ज्यामिति में मौजूद है। यह लोबचेव्स्की ज्यामिति या अन्य गैर-यूक्लिडियन ज्यामिति में नहीं होता है। गोले पर पाइथागोरस प्रमेय का कोई एनालॉग नहीं है। दो याम्योत्तर 90° का कोण बनाते हैं और भूमध्य रेखा एक गोले पर बंधी हुई एक समबाहु गोलाकार त्रिभुज है, जिसके तीनों कोण समकोण हैं। उसके लिए, हवाई जहाज़ की तरह नहीं।

पाइथागोरस प्रमेय का उपयोग करके, सूत्र का उपयोग करके बिंदुओं और समन्वय तल के बीच की दूरी की गणना करें

.

पाइथागोरस प्रमेय की खोज के बाद, यह सवाल उठा कि प्राकृतिक संख्याओं के सभी त्रिक कैसे खोजे जाएं जो समकोण त्रिभुज की भुजाएँ हो सकते हैं (फरमेट का अंतिम प्रमेय देखें)। उनकी खोज पाइथागोरस द्वारा की गई थी, लेकिन संख्याओं के ऐसे त्रिक को खोजने के कुछ सामान्य तरीके बेबीलोनियों को पहले से ही ज्ञात थे। क्यूनिफॉर्म गोलियों में से एक में 15 त्रिक होते हैं। इनमें त्रिक भी हैं जिनकी संख्या इतनी बड़ी है कि उन्हें चुनकर खोजने का प्रश्न ही नहीं उठता।

हिप्पोक्रेटिक फोसा

हिप्पोक्रेटिक लूना दो वृत्तों के चापों से घिरी हुई आकृतियाँ हैं, और, इसके अलावा, जैसे कि इन वृत्तों की सामान्य जीवा की त्रिज्या और लंबाई का उपयोग करके, एक कम्पास और एक शासक का उपयोग करके, कोई उनके समान आकार के वर्गों का निर्माण कर सकता है।

पाइथागोरस प्रमेय के अर्धवृत्तों के सामान्यीकरण से, यह निष्कर्ष निकलता है कि बाईं ओर के चित्र में दिखाए गए गुलाबी गांठों के क्षेत्रों का योग नीले त्रिकोण के क्षेत्रफल के बराबर है। इसलिए, यदि आप एक समद्विबाहु समकोण त्रिभुज लेते हैं, तो आपको दो छेद मिलेंगे, जिनमें से प्रत्येक का क्षेत्रफल त्रिभुज के आधे क्षेत्रफल के बराबर होगा। एक वृत्त को वर्गित करने की समस्या को हल करने का प्रयास करते हुए (प्राचीन काल की शास्त्रीय समस्याएं देखें), प्राचीन यूनानी गणितज्ञ हिप्पोक्रेट्स (5वीं शताब्दी ईसा पूर्व) ने कई और छेद खोजे, जिनके क्षेत्रफल सीधी रेखाओं के क्षेत्रफलों के रूप में व्यक्त किए गए हैं।

हिप्पोमार्जिनल लुनुले की पूरी सूची केवल 19वीं-20वीं शताब्दी में प्राप्त की गई थी। गैलोज़ सिद्धांत विधियों के उपयोग के लिए धन्यवाद।

सुनिश्चित करें कि आपको जो त्रिभुज दिया गया है वह एक समकोण त्रिभुज है, क्योंकि पाइथागोरस प्रमेय केवल समकोण त्रिभुजों पर लागू होता है।

• समकोण त्रिभुज में, तीन कोणों में से एक हमेशा 90 डिग्री का होता है।

एक समकोण त्रिभुज में एक समकोण को वक्र के बजाय एक वर्ग चिह्न द्वारा दर्शाया जाता है जो तिरछे कोणों का प्रतिनिधित्व करता है।त्रिभुज की भुजाओं को लेबल करें।