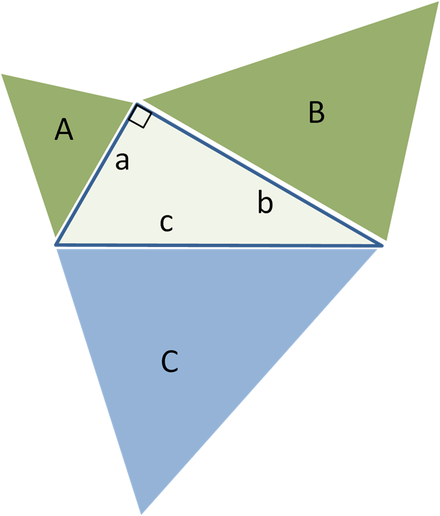
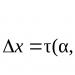Jakie są twierdzenia Pitagorasa? Prawy trójkąt

Geometria nie jest nauką prostą. Może być przydatna zarówno w szkolnym programie nauczania, jak i w prawdziwym życiu. Znajomość wielu wzorów i twierdzeń uprości obliczenia geometryczne. Jedną z najprostszych figur w geometrii jest trójkąt. Jedna z odmian trójkątów, równoboczna, ma swoje własne cechy.

Cechy trójkąta równobocznego

Z definicji trójkąt to wielościan, który ma trzy kąty i trzy boki. Jest to płaska dwuwymiarowa figura, jej właściwości są badane w szkole średniej. W zależności od rodzaju kąta rozróżnia się trójkąty ostre, rozwarte i prostokątne. Trójkąt prostokątny to figura geometryczna, w której jeden z kątów ma miarę 90°. Taki trójkąt ma dwie nogi (tworzą kąt prosty) i jedną przeciwprostokątną (jest przeciwna do kąta prostego). W zależności od znanych wielkości istnieją trzy proste sposoby obliczenia przeciwprostokątnej trójkąta prostokątnego.

Pierwszy sposób polega na znalezieniu przeciwprostokątnej trójkąta prostokątnego. Twierdzenie Pitagorasa

Twierdzenie Pitagorasa jest najstarszym sposobem obliczania dowolnego boku trójkąta prostokątnego. Brzmi to tak: „W trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg”. Zatem, aby obliczyć przeciwprostokątną, należy wyprowadzić pierwiastek kwadratowy z sumy dwóch nóg do kwadratu. Dla przejrzystości podano wzory i schemat.

Drugi sposób. Obliczanie przeciwprostokątnej przy użyciu 2 znanych wielkości: nogi i kąta przyległego

Jedna z właściwości trójkąta prostokątnego mówi, że stosunek długości przyprostokątnej do długości przeciwprostokątnej jest równy cosinusowi kąta między tą nogą a przeciwprostokątną. Nazwijmy znany nam kąt α. Teraz, dzięki dobrze znanej definicji, można łatwo sformułować wzór na obliczenie przeciwprostokątnej: Przeciwprostokątna = noga/cos(α)

Trzeci sposób. Obliczanie przeciwprostokątnej przy użyciu 2 znanych wielkości: nogi i kąta przeciwnego

Jeśli znany jest kąt przeciwny, można ponownie skorzystać z właściwości trójkąta prostokątnego. Stosunek długości nogi do przeciwprostokątnej jest równy sinusowi przeciwnego kąta. Nazwijmy jeszcze raz znany kąt α. Teraz do obliczeń użyjemy nieco innego wzoru:
Przeciwprostokątna = noga/grzech (α)

Przykłady pomagające zrozumieć formuły

Aby lepiej zrozumieć każdą z formuł, należy rozważyć przykłady ilustrujące. Załóżmy więc, że masz trójkąt prostokątny, w którym znajdują się następujące dane:

• Nogawka – 8 cm.
• Przyległy kąt cosα1 wynosi 0,8.
• Przeciwny kąt sinα2 wynosi 0,8.

Zgodnie z twierdzeniem Pitagorasa: Przeciwprostokątna = pierwiastek kwadratowy z (36+64) = 10 cm.
W zależności od wielkości nogi i przylegającego kąta: 8/0,8 = 10 cm.
W zależności od wielkości nogi i przeciwnego kąta: 8/0,8 = 10 cm.

Gdy zrozumiesz wzór, możesz łatwo obliczyć przeciwprostokątną na podstawie dowolnych danych.

Wideo: Twierdzenie Pitagorasa

(wg papirusu 6619 Muzeum Berlińskiego). Według Cantora harpedonapty, czyli „przeciągacze lin”, budowali kąty proste za pomocą trójkątów prostokątnych o bokach 3, 4 i 5.

Bardzo łatwo jest odtworzyć sposób ich budowy. Weźmy linę o długości 12 m i przywiążmy do niej kolorowy pasek w odległości 3 m od jednego końca i 4 m od drugiego. Kąt prosty będzie miał długość boków od 3 do 4 metrów. Harpedonaptom można by zarzucić, że ich metoda budowy staje się zbędna, jeśli zastosuje się na przykład drewniany kwadrat, którego używają wszyscy stolarze. Rzeczywiście znane są rysunki egipskie, w których znajduje się takie narzędzie - na przykład rysunki przedstawiające warsztat stolarski.

Nieco więcej wiadomo na temat twierdzenia Pitagorasa wśród Babilończyków. W jednym tekście sięgającym czasów Hammurabiego, czyli roku 2000 p.n.e. mi. , podano przybliżone obliczenie przeciwprostokątnej trójkąta prostokątnego. Z tego możemy wywnioskować, że w Mezopotamii przynajmniej w niektórych przypadkach byli w stanie wykonywać obliczenia z trójkątami prostokątnymi. Opierając się z jednej strony na obecnym stanie wiedzy o matematyce egipskiej i babilońskiej, a z drugiej strony na krytycznym badaniu źródeł greckich, Van der Waerden (matematyk holenderski) doszedł do wniosku, że istnieje duże prawdopodobieństwo, że twierdzenie o kwadracie przeciwprostokątnej było znane w Indiach już około XVIII wieku p.n.e. mi.

Około 400 roku p.n.e. BC, według Proklusa, Platon podał metodę znajdowania trójek pitagorejskich, łącząc algebrę i geometrię. Około 300 roku p.n.e. mi. Najstarszy aksjomatyczny dowód twierdzenia Pitagorasa pojawił się w Elementach Euklidesa.

Formuły

Wzór geometryczny:

Twierdzenie zostało pierwotnie sformułowane w następujący sposób:

Sformułowanie algebraiczne:

Oznacza to, że długość przeciwprostokątnej trójkąta oznacza się przez , a długości nóg przez i :

Oba sformułowania twierdzenia są równoważne, ale drugie sformułowanie jest bardziej elementarne i nie wymaga pojęcia pola. Oznacza to, że drugie stwierdzenie można zweryfikować, nie wiedząc nic o polu i mierząc jedynie długości boków trójkąta prostokątnego.

Odwrotne twierdzenie Pitagorasa:

Dowód

NA w tej chwili W literaturze naukowej odnotowano 367 dowodów tego twierdzenia. Prawdopodobnie twierdzenie Pitagorasa jest jedynym twierdzeniem z tak imponującą liczbą dowodów. Taką różnorodność można wytłumaczyć jedynie zasadniczym znaczeniem twierdzenia dla geometrii.

Oczywiście koncepcyjnie wszystkie można podzielić na niewielką liczbę klas. Najsłynniejsze z nich: dowody metodą powierzchniową, dowody aksjomatyczne i egzotyczne (np. z wykorzystaniem równań różniczkowych).

Przez podobne trójkąty

Poniższy dowód sformułowania algebraicznego jest najprostszym z dowodów, zbudowanym bezpośrednio z aksjomatów. W szczególności nie wykorzystuje pojęcia pola figury.

Pozwalać ABC istnieje trójkąt prostokątny z kątem prostym C. Narysujmy wysokość z C i oznacz jego podstawę przez H. Trójkąt ACH podobny do trójkąta ABC w dwóch rogach. Podobnie trójkąt CBH podobny ABC. Wprowadzając notację

dostajemy

Co jest równoważne

Dodając to, otrzymujemy

Dowody metodą powierzchniową

Poniższe dowody, pomimo pozornej prostoty, wcale nie są takie proste. Wszyscy posługują się właściwościami pola, których dowód jest bardziej złożony niż dowód samego twierdzenia Pitagorasa.

Dowód poprzez ekwidopełnienie

1. Ułóżmy cztery równe trójkąty prostokątne, jak pokazano na rysunku 1.
2. Czworokąt z bokami C jest kwadratem, ponieważ suma dwóch kątów ostrych wynosi 90°, a kąt prosty wynosi 180°.
3. Pole całej figury jest równe z jednej strony polu kwadratu o boku (a + b), a z drugiej strony sumie pól czterech trójkątów i obszar wewnętrznego placu.

co było do okazania

Dowód Euklidesa

Idea dowodu Euklidesa jest następująca: spróbujmy udowodnić, że połowa pola kwadratu zbudowanego na przeciwprostokątnej jest równa sumie połówek pól kwadratów zbudowanych na nogach, a następnie pól duży i dwa małe kwadraty są równe.

Spójrzmy na rysunek po lewej stronie. Na nim zbudowaliśmy kwadraty po bokach trójkąta prostokątnego i wyciągnęliśmy promień s z wierzchołka kąta prostego C prostopadle do przeciwprostokątnej AB, przecina on zbudowany na przeciwprostokątnej kwadrat ABIK na dwa prostokąty - BHJI i HAKJ, odpowiednio. Okazuje się, że pola tych prostokątów są dokładnie równe obszarom kwadratów zbudowanych na odpowiednich nogach.

Spróbujmy udowodnić, że pole kwadratu DECA jest równe polu prostokąta AHJK. W tym celu skorzystamy z obserwacji pomocniczej: Pole trójkąta o tej samej wysokości i podstawie co dany prostokąt jest równy połowie pola danego prostokąta. Jest to konsekwencja określenia pola trójkąta jako połowy iloczynu podstawy i wysokości. Z tej obserwacji wynika, że ​​pole trójkąta ACK jest równe polu trójkąta AHK (niepokazanego na rysunku), które z kolei jest równe połowie pola prostokąta AHJK.

Udowodnimy teraz, że pole trójkąta ACK jest również równe połowie pola kwadratu DECA. Jedyne, co należy w tym celu zrobić, to udowodnić równość trójkątów ACK i BDA (ponieważ pole trójkąta BDA jest równe połowie pola kwadratu zgodnie z powyższą właściwością). Ta równość jest oczywista: trójkąty są równe po dwóch bokach i kącie między nimi. Mianowicie - AB=AK, AD=AC - równość kątów CAK i BAD łatwo udowodnić metodą ruchu: obracamy trójkąt CAK o 90° przeciwnie do ruchu wskazówek zegara, wtedy jest oczywiste, że odpowiednie boki dwóch trójkątów w pytanie będzie zbieżne (ponieważ kąt przy wierzchołku kwadratu wynosi 90°).

Rozumowanie równości pól kwadratu BCFG i prostokąta BHJI jest całkowicie podobne.

W ten sposób udowodniliśmy, że pole kwadratu zbudowanego na przeciwprostokątnej składa się z pól kwadratów zbudowanych na nogach. Ideę tego dowodu dodatkowo ilustruje powyższa animacja.

Dowód Leonarda da Vinci

Głównymi elementami dowodu są symetria i ruch.

Rozważmy rysunek, jak widać z symetrii, odcinek przecina kwadrat na dwie identyczne części (ponieważ trójkąty mają równą konstrukcję).

Stosując obrót punktu o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara, widzimy równość zacienionych figur i.

Teraz jest jasne, że obszar zacienionej przez nas figury jest równy sumie połowy pól małych kwadratów (zbudowanych na nogach) i pola pierwotnego trójkąta. Z drugiej strony jest on równy połowie pola dużego kwadratu (zbudowanego na przeciwprostokątnej) plus pole pierwotnego trójkąta. Zatem połowa sumy pól małych kwadratów jest równa połowie pola dużego kwadratu, a zatem suma pól kwadratów zbudowanych na nogach jest równa powierzchni kwadratu zbudowanego na przeciwprostokątna.

Dowód metodą nieskończenie małą

Poniższy dowód wykorzystujący równania różniczkowe przypisuje się często słynnemu angielskiemu matematykowi Hardy’emu, który żył w pierwszej połowie XX wieku.

Patrząc na rysunek pokazany na rysunku i obserwując zmianę strony A, możemy zapisać następującą zależność dla nieskończenie małych przyrostów boku Z I A(używając podobieństwa trójkątów):

Stosując metodę separacji zmiennych, znajdujemy

Bardziej ogólne wyrażenie zmiany przeciwprostokątnej w przypadku przyrostów po obu stronach

Całkując to równanie i korzystając z warunków początkowych, otrzymujemy

W ten sposób dochodzimy do pożądanej odpowiedzi

Jak łatwo zauważyć, zależność kwadratowa w ostatecznym wzorze pojawia się na skutek liniowej proporcjonalności pomiędzy bokami trójkąta a przyrostami, natomiast suma jest powiązana z niezależnymi wkładami przyrostów różnych nóg.

Prostszy dowód można uzyskać, jeśli założymy, że jedna z nóg nie doznaje przyrostu (w tym przypadku noga). Następnie dla stałej całkowania otrzymujemy

Odmiany i uogólnienia

Podobne kształty geometryczne z trzech stron

Uogólnienie dla podobnych trójkątów, obszar zielonych kształtów A + B = obszar niebieskiego C

Twierdzenie Pitagorasa wykorzystujące podobne trójkąty prostokątne

Euklides w swojej pracy uogólnił twierdzenie Pitagorasa Początki, rozszerzając pola kwadratów po bokach do obszarów podobnych figur geometrycznych:

Jeśli zbudujemy podobne figury geometryczne (patrz geometria euklidesowa) na bokach trójkąta prostokątnego, wówczas suma dwóch mniejszych figur będzie równa powierzchni większej figury.

Główną ideą tego uogólnienia jest to, że pole takiej figury geometrycznej jest proporcjonalne do kwadratu dowolnego jej wymiaru liniowego, a w szczególności do kwadratu długości dowolnego boku. Dlatego dla podobnych liczb z obszarami A, B I C zbudowany na bokach o długości A, B I C, mamy:

Ale zgodnie z twierdzeniem Pitagorasa, A 2 + B 2 = C 2 wtedy A + B = C.

I odwrotnie, jeśli możemy to udowodnić A + B = C dla trzech podobnych figur geometrycznych bez korzystania z twierdzenia Pitagorasa, wówczas możemy udowodnić samo twierdzenie, poruszając się w przeciwnym kierunku. Na przykład początkowy środkowy trójkąt można ponownie wykorzystać jako trójkąt C na przeciwprostokątnej i dwa podobne trójkąty prostokątne ( A I B), zbudowane na dwóch pozostałych bokach, które powstają poprzez podzielenie środkowego trójkąta przez jego wysokość. Zatem suma pól dwóch mniejszych trójkątów jest oczywiście równa polu trzeciego A + B = C i wykonując poprzedni dowód w odwrotnej kolejności, otrzymujemy twierdzenie Pitagorasa a 2 + b 2 = c 2 .

Twierdzenie cosinus

Twierdzenie Pitagorasa jest szczególnym przypadkiem bardziej ogólnego twierdzenia o cosinus, które wiąże długości boków w dowolnym trójkącie:

gdzie θ jest kątem między bokami A I B.

Jeśli θ wynosi 90 stopni, to cos θ = 0, a wzór upraszcza się do zwykłego twierdzenia Pitagorasa.

Wolny trójkąt

Do dowolnego wybranego narożnika dowolnego trójkąta z bokami a, b, c Wpiszmy trójkąt równoramienny w taki sposób, aby równe kąty przy jego podstawie θ były równe wybranemu kątowi. Załóżmy, że wybrany kąt θ leży naprzeciwko wyznaczonego boku C. W rezultacie otrzymaliśmy trójkąt ABD o kącie θ, który leży naprzeciwko boku A i imprezy R. Drugi trójkąt jest utworzony przez kąt θ, który znajduje się naprzeciwko boku B i imprezy Z długość S jak pokazano na rysunku. Thabit Ibn Qurra argumentował, że boki tych trzech trójkątów są powiązane w następujący sposób:

Gdy kąt θ zbliża się do π/2, podstawa trójkąta równoramiennego staje się mniejsza, a dwa boki r i s coraz mniej na siebie zachodzą. Gdy θ = π/2, ADB staje się trójkątem prostokątnym, R + S = C i otrzymujemy początkowe twierdzenie Pitagorasa.

Rozważmy jeden z argumentów. Trójkąt ABC ma takie same kąty jak trójkąt ABD, ale w odwrotnej kolejności. (Obydwa trójkąty mają wspólny kąt w wierzchołku B, oba mają kąt θ i ten sam trzeci kąt, w oparciu o sumę kątów trójkąta) Odpowiednio ABC jest podobne do odbicia ABD trójkąta DBA, ponieważ pokazano na dolnym rysunku. Zapiszmy zależność pomiędzy przeciwległymi stronami i tymi sąsiadującymi z kątem θ,

Również odbicie innego trójkąta,

Pomnóżmy ułamki i dodajmy te dwa stosunki:

co było do okazania

Uogólnienie dla dowolnych trójkątów za pomocą równoległoboków

Uogólnienie dla dowolnych trójkątów,
teren zielony działka = powierzchnia niebieski

Dowód tezy, że na powyższym rysunku

Dokonajmy dalszego uogólnienia dla trójkątów innych niż prostokątne, używając równoległoboków z trzech stron zamiast kwadratów. (kwadraty są przypadkiem szczególnym.) Górny rysunek pokazuje, że w przypadku ostrego trójkąta pole równoległoboku na długim boku jest równe sumie równoległoboków na pozostałych dwóch bokach, pod warunkiem, że równoległobok na długim bok jest skonstruowany jak pokazano na rysunku (wymiary wskazane strzałkami są takie same i wyznaczają boki dolnego równoległoboku). To zastąpienie kwadratów równoległobokami wykazuje wyraźne podobieństwo do początkowego twierdzenia Pitagorasa, które, jak się uważa, zostało sformułowane przez Pappusa z Aleksandrii w 4 roku naszej ery. mi.

Dolny rysunek pokazuje postęp dowodu. Spójrzmy na lewą stronę trójkąta. Lewy zielony równoległobok ma takie samo pole jak lewa strona niebieskiego równoległoboku, ponieważ mają tę samą podstawę B i wysokość H. Dodatkowo lewy zielony równoległobok ma takie samo pole jak lewy zielony równoległobok na górnym obrazku, ponieważ mają one wspólną podstawę (lewy górny bok trójkąta) i wspólną wysokość prostopadłą do tej strony trójkąta. Stosując podobne rozumowanie dla prawej strony trójkąta, udowodnimy, że dolny równoległobok ma takie samo pole jak dwa zielone równoległoboki.

Liczby zespolone

Twierdzenie Pitagorasa służy do obliczania odległości między dwoma punktami w kartezjańskim układzie współrzędnych i twierdzenie to jest ważne dla wszystkich prawdziwych współrzędnych: odległość S między dwoma punktami ( a, b) I ( płyta CD) równa się

Ze wzorem nie ma problemów, jeśli liczby zespolone potraktujemy jako wektory ze składnikami rzeczywistymi X + ja y = (X, y). . Na przykład odległość S pomiędzy 0 + 1 I i 1 + 0 I obliczany jako moduł wektora (0, 1) − (1, 0) = (−1, 1), Lub

Jednak w przypadku operacji na wektorach o złożonych współrzędnych konieczne jest wprowadzenie pewnych ulepszeń do wzoru Pitagorasa. Odległość między punktami o liczbach zespolonych ( A, B) I ( C, D); A, B, C, I D wszystkie złożone, formułujemy przy użyciu wartości bezwzględnych. Dystans S w oparciu o różnicę wektorów (A − C, B − D) w następującej formie: niech różnica A − C = P+ja Q, Gdzie P- rzeczywista część różnicy, Q jest częścią urojoną i i = √(−1). Podobnie niech B − D = R+ja S. Następnie:

gdzie jest zespoloną liczbą sprzężoną dla . Na przykład odległość między punktami (A, B) = (0, 1) I (C, D) = (I, 0) , obliczmy różnicę (A − C, B − D) = (−I, 1) a wynik wyniósłby 0, gdyby nie zastosowano złożonych koniugatów. Dlatego korzystając z ulepszonej formuły, otrzymujemy

Moduł jest zdefiniowany w następujący sposób:

Stereometria

Znaczącym uogólnieniem twierdzenia Pitagorasa dla przestrzeni trójwymiarowej jest twierdzenie de Goya, nazwane na cześć J.-P. de Gois: jeśli czworościan ma kąt prosty (jak w sześcianie), wówczas kwadrat pola powierzchni przeciwnej do kąta prostego jest równy sumie kwadratów pól pozostałych trzech ścian. Wniosek ten można podsumować następująco: „ N-wymiarowe twierdzenie Pitagorasa":

Twierdzenie Pitagorasa w przestrzeni trójwymiarowej wiąże przekątną AD z trzema bokami.

Inne uogólnienie: Twierdzenie Pitagorasa można zastosować do stereometrii w następującej formie. Rozważmy prostokątny równoległościan, jak pokazano na rysunku. Znajdźmy długość przekątnej BD, korzystając z twierdzenia Pitagorasa:

gdzie trzy boki tworzą trójkąt prostokątny. Używamy poziomej przekątnej BD i pionowej krawędzi AB, aby znaleźć długość przekątnej AD, w tym celu ponownie używamy twierdzenia Pitagorasa:

lub jeśli zapiszemy wszystko w jednym równaniu:

Wynik ten jest trójwymiarowym wyrażeniem służącym do określenia wielkości wektora w(przekątna AD), wyrażona jako jej składowe prostopadłe ( w k ) (trzy wzajemnie prostopadłe boki):

Równanie to można uznać za uogólnienie twierdzenia Pitagorasa dla przestrzeni wielowymiarowej. Jednak rezultatem jest w rzeczywistości nic innego jak wielokrotne zastosowanie twierdzenia Pitagorasa do ciągu trójkątów prostokątnych w kolejnych prostopadłych płaszczyznach.

Przestrzeń wektorowa

W przypadku ortogonalnego układu wektorów zachodzi równość, zwana także twierdzeniem Pitagorasa:

Jeżeli - są to rzuty wektora na osie współrzędnych, to wzór ten pokrywa się z odległością euklidesową - i oznacza, że ​​długość wektora jest równa pierwiastkowi kwadratowemu z sumy kwadratów jego składowych.

Analogię tej równości w przypadku nieskończonego układu wektorów nazywamy równością Parsevala.

Geometria nieeuklidesowa

Twierdzenie Pitagorasa wywodzi się z aksjomatów geometrii euklidesowej i w rzeczywistości nie obowiązuje dla geometrii nieeuklidesowej w formie, w jakiej zostało zapisane powyżej. (Oznacza to, że twierdzenie Pitagorasa okazuje się być swego rodzaju odpowiednikiem postulatu równoległości Euklidesa) Innymi słowy, w geometrii nieeuklidesowej związek między bokami trójkąta z konieczności będzie miał inną formę niż twierdzenie Pitagorasa. Na przykład w geometrii sferycznej wszystkie trzy boki trójkąta prostokątnego (powiedzmy A, B I C), które ograniczają oktantę (ósmą część) sfery jednostkowej, mają długość π/2, co jest sprzeczne z twierdzeniem Pitagorasa, ponieważ A 2 + B 2 ≠ C 2 .

Rozważmy tutaj dwa przypadki geometrii nieeuklidesowej - geometrię sferyczną i hiperboliczną; w obu przypadkach, jeśli chodzi o przestrzeń euklidesową dla trójkątów prostokątnych, wynik, który zastępuje twierdzenie Pitagorasa, wynika z twierdzenia cosinus.

Jednakże twierdzenie Pitagorasa pozostaje ważne dla geometrii hiperbolicznej i eliptycznej, jeśli wymóg prostokątności trójkąta zostanie zastąpiony warunkiem, że suma dwóch kątów trójkąta musi być równa trzeciemu, powiedzmy A+B = C. Wtedy zależność między bokami wygląda następująco: suma pól okręgów o średnicach A I B równy obszarowi koła o średnicy C.

Geometria sferyczna

Dla dowolnego trójkąta prostokątnego na kuli o promieniu R(na przykład, jeśli kąt γ w trójkącie jest prosty) z bokami A, B, C Relacja pomiędzy stronami będzie wyglądać następująco:

Równość tę można wyprowadzić jako szczególny przypadek twierdzenia o sferycznym cosinusie, które obowiązuje dla wszystkich trójkątów sferycznych:

gdzie cosh jest cosinusem hiperbolicznym. Wzór ten jest szczególnym przypadkiem twierdzenia o cosinusie hiperbolicznym, które obowiązuje dla wszystkich trójkątów:

gdzie γ jest kątem, którego wierzchołek jest przeciwny do boku C.

Gdzie G ja zwany tensorem metrycznym. Może to być funkcja położenia. Ogólnym przykładem takich przestrzeni krzywoliniowych jest geometria riemannowska. To sformułowanie jest również odpowiednie dla przestrzeni euklidesowej przy użyciu współrzędnych krzywoliniowych. Na przykład dla współrzędnych biegunowych:

Grafika wektorowa

Twierdzenie Pitagorasa łączy dwa wyrażenia określające wielkość iloczynu wektorowego. Jedno podejście do definiowania iloczynu krzyżowego wymaga, aby spełniał on równanie:

W tej formule używany jest iloczyn skalarny. Prawa strona równania nazywana jest wyznacznikiem Grama A I B, który jest równy obszarowi równoległoboku utworzonego przez te dwa wektory. W oparciu o ten wymóg, a także wymóg, aby iloczyn wektorowy był prostopadły do ​​jego składników A I B wynika z tego, że poza trywialnymi przypadkami z przestrzeni 0 i 1 wymiarowej iloczyn poprzeczny definiuje się tylko w trzech i siedmiu wymiarach. Korzystamy z definicji kąta w N-przestrzeń wymiarowa:

Ta właściwość iloczynu krzyżowego określa jego wielkość w następujący sposób:

Poprzez podstawową tożsamość trygonometryczną Pitagorasa uzyskujemy inną formę zapisu jego wartości:

Alternatywne podejście do definiowania iloczynu krzyżowego wykorzystuje wyrażenie określające jego wielkość. Następnie rozumując w odwrotnej kolejności otrzymujemy związek z iloczynem skalarnym:

Zobacz także

Notatki

1. Temat historyczny: Twierdzenie Pitagorasa w matematyce babilońskiej
2. ( , s. 351) s. 351
3. ( , tom I, s. 144)
4. Omówienie faktów historycznych znajduje się w (, s. 351) s. 351
5. Kurt Von Fritz (kwiecień 1945). „Odkrycie niewspółmierności przez Hippasosa z Metapontum”. Roczniki matematyki, seria druga(Roczniki matematyki) 46 (2): 242–264.
6. Lewis Carroll, „Historia z węzłami”, M., Mir, 1985, s. 25. 7
7. Asgera Aaboe Epizody z początków historii matematyki. – Mathematical Association of America, 1997. – s. 51. – ISBN 0883856131
8. Propozycja Pythona autorstwa Elishy Scott Loomis
9. Euklidesa Elementy: Księga VI, Twierdzenie VI 31: „W trójkątach prostokątnych figura po stronie odpowiadającej kątowi prostemu jest równa podobnym i podobnie opisanym figurom po bokach zawierających kąt prosty”.
10. Lawrence S. Leff cytowana praca. - Seria edukacyjna Barrona - str. 326. - ISBN 0764128922
11. Howard Whitley Ewa§4.8:...uogólnienie twierdzenia Pitagorasa // Wielkie momenty w matematyce (przed 1650 rokiem). – Mathematical Association of America, 1983. – s. 41. – ISBN 0883853108
12. Tâbit ibn Qorra (pełne imię i nazwisko Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 ne) był lekarzem mieszkającym w Bagdadzie, który pisał obszernie na temat elementów Euklidesa i innych przedmiotów matematycznych.
13. Aydin Sayili (marzec 1960). „Uogólnienie twierdzenia Pitagorasa Thâbita ibn Qurry”. Izyda 51 (1): 35–37. DOI:10.1086/348837.
14. Judith D. Sally, Paul SallyĆwiczenie 2.10 (ii) // Cytowana praca. - s. 62. - ISBN 0821844032
15. Szczegóły takiej konstrukcji zob George'a Jenningsa Rysunek 1.32: Uogólnione twierdzenie Pitagorasa // Nowoczesna geometria z zastosowaniami: ze 150 cyframi. - 3. - Springer, 1997. - s. 23. - ISBN 038794222X
16. Arlen Brown, Carl M. Pearcy Przedmiot C: Norma dla dowolnego N-tuple ... // Wprowadzenie do analizy . - Springer, 1995. - s. 124. - ISBN 0387943692 Patrz także strony 47-50.
17. Alfreda Graya, Elsy Abbeny i Simona Salamona Nowoczesna geometria różniczkowa krzywych i powierzchni z Mathematicą. - 3. - CRC Press, 2006. - s. 194. - ISBN 1584884487
18. Rajendrę Bhatię Analiza macierzowa. - Springer, 1997. - s. 21. - ISBN 0387948465
19. Stephena W. Hawkinga cytowana praca. - 2005. - s. 4. - ISBN 0762419229
20. Erica W. Weissteina CRC zwięzła encyklopedia matematyki. - 2. - 2003. - s. 2147. - ISBN 1584883472
21. Aleksander R. Pruss

Twierdzenie Pitagorasa: Suma pól kwadratów spoczywających na nogach ( A I B), równy polu kwadratu zbudowanego na przeciwprostokątnej ( C).

Wzór geometryczny:

Twierdzenie zostało pierwotnie sformułowane w następujący sposób:

Sformułowanie algebraiczne:

To znaczy, oznaczając długość przeciwprostokątnej trójkąta przez C i długości nóg A I B :

Oba sformułowania twierdzenia są równoważne, ale drugie sformułowanie jest bardziej elementarne i nie wymaga pojęcia pola. Oznacza to, że drugie stwierdzenie można zweryfikować, nie wiedząc nic o polu i mierząc jedynie długości boków trójkąta prostokątnego.

Odwrotne twierdzenie Pitagorasa:

Dowód

Obecnie w literaturze naukowej odnotowano 367 dowodów tego twierdzenia. Prawdopodobnie twierdzenie Pitagorasa jest jedynym twierdzeniem z tak imponującą liczbą dowodów. Taką różnorodność można wytłumaczyć jedynie zasadniczym znaczeniem twierdzenia dla geometrii.

Oczywiście koncepcyjnie wszystkie można podzielić na niewielką liczbę klas. Najsłynniejsze z nich: dowody metodą powierzchniową, dowody aksjomatyczne i egzotyczne (np. z wykorzystaniem równań różniczkowych).

Przez podobne trójkąty

Poniższy dowód sformułowania algebraicznego jest najprostszym z dowodów, zbudowanym bezpośrednio z aksjomatów. W szczególności nie wykorzystuje pojęcia pola figury.

Pozwalać ABC istnieje trójkąt prostokątny z kątem prostym C. Narysujmy wysokość z C i oznacz jego podstawę przez H. Trójkąt ACH podobny do trójkąta ABC w dwóch rogach. Podobnie trójkąt CBH podobny ABC. Wprowadzając notację

dostajemy

Co jest równoważne

Dodając to, otrzymujemy

Dowody metodą powierzchniową

Poniższe dowody, pomimo pozornej prostoty, wcale nie są takie proste. Wszyscy posługują się właściwościami pola, których dowód jest bardziej złożony niż dowód samego twierdzenia Pitagorasa.

Dowód poprzez ekwidopełnienie

1. Ułóżmy cztery równe trójkąty prostokątne, jak pokazano na rysunku 1.
2. Czworokąt z bokami C jest kwadratem, ponieważ suma dwóch kątów ostrych wynosi 90°, a kąt prosty wynosi 180°.
3. Pole całej figury jest równe z jednej strony polu kwadratu o boku (a + b), a z drugiej strony sumie pól czterech trójkątów i dwóch wewnętrznych kwadraty.

co było do okazania

Dowody poprzez równoważność

Elegancki dowód z użyciem permutacji

Przykład jednego z takich dowodów pokazano na rysunku po prawej stronie, na którym kwadrat zbudowany na przeciwprostokątnej zostaje przestawiony na dwa kwadraty zbudowane na ramionach.

Dowód Euklidesa

Rysunek do dowodu Euklidesa

Ilustracja do dowodu Euklidesa

Idea dowodu Euklidesa jest następująca: spróbujmy udowodnić, że połowa pola kwadratu zbudowanego na przeciwprostokątnej jest równa sumie połówek pól kwadratów zbudowanych na nogach, a następnie pól duży i dwa małe kwadraty są równe.

Spójrzmy na rysunek po lewej stronie. Na nim zbudowaliśmy kwadraty po bokach trójkąta prostokątnego i wyciągnęliśmy promień s z wierzchołka kąta prostego C prostopadle do przeciwprostokątnej AB, przecina on zbudowany na przeciwprostokątnej kwadrat ABIK na dwa prostokąty - BHJI i HAKJ, odpowiednio. Okazuje się, że pola tych prostokątów są dokładnie równe obszarom kwadratów zbudowanych na odpowiednich nogach.

Spróbujmy udowodnić, że pole kwadratu DECA jest równe polu prostokąta AHJK. W tym celu skorzystamy z obserwacji pomocniczej: Pole trójkąta o tej samej wysokości i podstawie co dany prostokąt jest równy połowie pola danego prostokąta. Jest to konsekwencja określenia pola trójkąta jako połowy iloczynu podstawy i wysokości. Z tej obserwacji wynika, że ​​pole trójkąta ACK jest równe polu trójkąta AHK (niepokazanego na rysunku), które z kolei jest równe połowie pola prostokąta AHJK.

Udowodnimy teraz, że pole trójkąta ACK jest również równe połowie pola kwadratu DECA. Jedyne, co należy w tym celu zrobić, to udowodnić równość trójkątów ACK i BDA (ponieważ pole trójkąta BDA jest równe połowie pola kwadratu zgodnie z powyższą właściwością). Ta równość jest oczywista, trójkąty są równe po obu stronach i kąt między nimi. Mianowicie - AB=AK,AD=AC - równość kątów CAK i BAD łatwo udowodnić metodą ruchu: obracamy trójkąt CAK o 90° przeciwnie do ruchu wskazówek zegara, wtedy jest oczywiste, że odpowiednie boki dwóch trójkątów w pytanie będzie zbieżne (ponieważ kąt przy wierzchołku kwadratu wynosi 90°).

Rozumowanie równości pól kwadratu BCFG i prostokąta BHJI jest całkowicie podobne.

W ten sposób udowodniliśmy, że pole kwadratu zbudowanego na przeciwprostokątnej składa się z pól kwadratów zbudowanych na nogach. Ideę tego dowodu dodatkowo ilustruje powyższa animacja.

Dowód Leonarda da Vinci

Dowód Leonarda da Vinci

Głównymi elementami dowodu są symetria i ruch.

Rozważmy rysunek, jak widać z symetrii, segment CI przecina kwadrat ABHJ na dwie identyczne części (ponieważ trójkąty ABC I JHI jednakowe konstrukcyjnie). Stosując obrót o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara, widzimy równość zacieniowanych figur CAJI I GDAB . Teraz jest jasne, że pole zacienionej przez nas figury jest równe sumie połowy pól kwadratów zbudowanych na nogach i pola pierwotnego trójkąta. Z drugiej strony jest on równy połowie pola kwadratu zbudowanego na przeciwprostokątnej plus pole pierwotnego trójkąta. Ostatni krok dowodu pozostawiamy czytelnikowi.

Dowód metodą nieskończenie małą

Poniższy dowód wykorzystujący równania różniczkowe przypisuje się często słynnemu angielskiemu matematykowi Hardy’emu, który żył w pierwszej połowie XX wieku.

Patrząc na rysunek pokazany na rysunku i obserwując zmianę strony A, możemy zapisać następującą zależność dla nieskończenie małych przyrostów boku Z I A(używając podobieństwa trójkątów):

Dowód metodą nieskończenie małą

Stosując metodę separacji zmiennych, znajdujemy

Bardziej ogólne wyrażenie zmiany przeciwprostokątnej w przypadku przyrostów po obu stronach

Całkując to równanie i korzystając z warunków początkowych, otrzymujemy

W ten sposób dochodzimy do pożądanej odpowiedzi

Jak łatwo zauważyć, zależność kwadratowa w ostatecznym wzorze pojawia się na skutek liniowej proporcjonalności pomiędzy bokami trójkąta a przyrostami, natomiast suma jest powiązana z niezależnymi wkładami przyrostów różnych nóg.

Prostszy dowód można uzyskać, jeśli założymy, że jedna z nóg nie doznaje przyrostu (w tym przypadku noga B). Następnie dla stałej całkowania otrzymujemy

Odmiany i uogólnienia

• Jeśli zamiast kwadratów skonstruujemy po bokach inne podobne figury, wówczas prawdziwe jest następujące uogólnienie twierdzenia Pitagorasa: W trójkącie prostokątnym suma pól podobnych figur zbudowanych na bokach jest równa powierzchni figury zbudowanej na przeciwprostokątnej. Zwłaszcza:
  • Suma pól trójkątów foremnych zbudowanych na nogach jest równa powierzchni trójkąta foremnego zbudowanego na przeciwprostokątnej.
  • Suma pól półkola zbudowanego na nogach (jak na średnicy) jest równa polu półkola zbudowanego na przeciwprostokątnej. Na tym przykładzie wykazano właściwości figur ograniczonych łukami dwóch okręgów i zwanych lunulami Hipokratesa.

Historia

Chu-pei 500–200 pne. Po lewej stronie napis: suma kwadratów długości wysokości i podstawy jest kwadratem długości przeciwprostokątnej.

Starożytna chińska książka Chu-pei mówi o trójkącie pitagorejskim o bokach 3, 4 i 5: W tej samej książce znajduje się rysunek, który pokrywa się z jednym z rysunków hinduskiej geometrii Bashary.

Cantor (największy niemiecki historyk matematyki) uważa, że ​​równość 3² + 4² = 5² była znana Egipcjanom już około 2300 roku p.n.e. e. za czasów króla Amenemheta I (według papirusu 6619 z Muzeum Berlińskiego). Według Cantora harpedonapty, czyli „przeciągacze lin”, budowali kąty proste, korzystając z trójkątów prostokątnych o bokach 3, 4 i 5.

Bardzo łatwo jest odtworzyć sposób ich budowy. Weźmy linę o długości 12 m i przywiążmy do niej kolorowy pasek w odległości 3 m. z jednego końca i 4 metry od drugiego. Kąt prosty będzie zawarty pomiędzy bokami o długości 3 i 4 metrów. Można by zarzucić harpedonaptianom, że ich metoda budowy staje się zbędna, jeśli użyje się na przykład drewnianego kwadratu, którego używają wszyscy stolarze. Rzeczywiście znane są rysunki egipskie, w których znajduje się takie narzędzie, na przykład rysunki przedstawiające warsztat stolarski.

Nieco więcej wiadomo na temat twierdzenia Pitagorasa wśród Babilończyków. W jednym tekście sięgającym czasów Hammurabiego, czyli roku 2000 p.n.e. e. podano przybliżone obliczenie przeciwprostokątnej trójkąta prostokątnego. Z tego możemy wywnioskować, że w Mezopotamii przynajmniej w niektórych przypadkach byli w stanie wykonywać obliczenia z trójkątami prostokątnymi. Opierając się z jednej strony na obecnym stanie wiedzy o matematyce egipskiej i babilońskiej, a z drugiej strony na krytycznym badaniu źródeł greckich, Van der Waerden (matematyk holenderski) doszedł do następującego wniosku:

Literatura

W języku rosyjskim

• Skopets Z. A. Miniatury geometryczne. M., 1990
• Elenski Szch.Śladami Pitagorasa. M., 1961
• Van der Waerden B. L. Przebudzenie nauki. Matematyka starożytnego Egiptu, Babilonu i Grecji. M., 1959
• Glazer G.I. Historia matematyki w szkole. M., 1982
• W. Litzman, „Twierdzenie Pitagorasa” M., 1960.
  • Strona o twierdzeniu Pitagorasa z dużą liczbą dowodów, materiał zaczerpnięty z książki V. Litzmanna, duża liczba rysunków zaprezentowanych w formie oddzielnych plików graficznych.
• Twierdzenie Pitagorasa i trójki Pitagorasa rozdział z książki D. V. Anosowa „Spojrzenie na matematykę i coś z niej”
• O twierdzeniu Pitagorasa i metodach jego dowodzenia G. Glaser, akademik Rosyjskiej Akademii Pedagogicznej, Moskwa

W języku angielskim

• Twierdzenie Pitagorasa w WolframMathWorld
• Cut-The-Knot, sekcja dotycząca twierdzenia Pitagorasa, około 70 dowodów i obszerne informacje dodatkowe (w języku angielskim)

Fundacja Wikimedia.

2010.

Twierdzenie Pitagorasa jest najważniejszym stwierdzeniem geometrii. Twierdzenie jest sformułowane w następujący sposób: pole kwadratu zbudowanego na przeciwprostokątnej trójkąta prostokątnego jest równe sumie pól kwadratów zbudowanych na jego nogach.

Odkrycie tego stwierdzenia przypisuje się zwykle starożytnemu greckiemu filozofowi i matematykowi Pitagorasowi (VI wiek p.n.e.). Jednak badanie babilońskich tabliczek klinowych i starożytnych chińskich rękopisów (kopii jeszcze starszych rękopisów) wykazało, że stwierdzenie to było znane na długo przed Pitagorasem, być może tysiąc lat przed nim. Zasługą Pitagorasa było to, że odkrył dowód tego twierdzenia.

Jednak przez dwa tysiące lat nie używano tego dowodu wizualnego, ale bardziej złożonego dowodu wymyślonego przez Euklidesa, który umieszczono w jego słynnej książce „Elementy” (patrz Euklides i jego „Elementy”), Euklides obniżył wysokość od wierzchołka kąta prostego do przeciwprostokątnej i udowodnił, że jej kontynuacja dzieli kwadrat zbudowany na przeciwprostokątnej na dwa prostokąty, których pola są równe polam odpowiednich kwadratów zbudowanych na nogach (ryc. 3). Rysunek użyty do udowodnienia tego twierdzenia jest żartobliwie nazywany „spodami pitagorejskimi”. Przez długi czas uznawany był za jeden z symboli nauk matematycznych.

Obecnie znanych jest kilkadziesiąt różnych dowodów twierdzenia Pitagorasa. Niektóre z nich opierają się na podziale kwadratów, w którym kwadrat zbudowany na przeciwprostokątnej składa się z części wchodzących w skład podziałów kwadratów zbudowanych na nogach; inne - na uzupełnienie równych liczb; trzeci - na tym, że wysokość obniżona z wierzchołka kąta prostego do przeciwprostokątnej dzieli trójkąt prostokątny na dwa podobne do niego trójkąty.

Twierdzenie Pitagorasa leży u podstaw większości obliczeń geometrycznych. Już w starożytnym Babilonie używano go do obliczania długości wysokości trójkąta równoramiennego z długości podstawy i boku, strzałki odcinka ze średnicy koła i długości cięciwy oraz ustalania zależności pomiędzy elementami niektórych wielokątów foremnych. Korzystając z twierdzenia Pitagorasa, udowadniamy jego uogólnienie, które pozwala nam obliczyć długość boku leżącego naprzeciw kąta ostrego lub rozwartego:

Z tego uogólnienia wynika, że ​​obecność kąta prostego w jest nie tylko warunkiem wystarczającym, ale i koniecznym, aby równość była spełniona. Ze wzoru (1) wynika zależność między długościami przekątnych i boków równoległoboku, za pomocą którego łatwo jest znaleźć długość środkowej trójkąta na podstawie długości jego boków.

Na podstawie twierdzenia Pitagorasa wyprowadza się wzór wyrażający pole dowolnego trójkąta przez długości jego boków (patrz wzór Herona). Oczywiście do rozwiązania różnych problemów praktycznych wykorzystano także twierdzenie Pitagorasa.

Zamiast kwadratów można budować dowolne podobne figury (trójkąty równoboczne, półkola itp.) na bokach trójkąta prostokątnego. W tym przypadku pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na nogach. Kolejne uogólnienie wiąże się z przejściem z płaszczyzny do przestrzeni. Formułuje się go w następujący sposób: kwadrat długości przekątnej równoległościanu prostokątnego jest równy sumie kwadratów jego wymiarów (długość, szerokość i wysokość). Podobne twierdzenie jest prawdziwe w przypadkach wielowymiarowych, a nawet nieskończenie wymiarowych.

Twierdzenie Pitagorasa istnieje tylko w geometrii euklidesowej. Nie występuje ani w geometrii Łobaczewskiego, ani w innych geometriach nieeuklidesowych. Nie ma odpowiednika twierdzenia Pitagorasa na kuli. Dwa południki tworzące kąt 90° i równik ograniczają na kuli równoboczny trójkąt sferyczny, którego wszystkie trzy kąty są kątami prostymi. Dla niego, nie jak w samolocie.

Korzystając z twierdzenia Pitagorasa, oblicz odległość między punktami a płaszczyzną współrzędnych, korzystając ze wzoru

.

Po odkryciu twierdzenia Pitagorasa pojawiło się pytanie, jak znaleźć wszystkie trójki liczb naturalnych, które mogą być bokami trójkątów prostokątnych (patrz ostatnie twierdzenie Fermata). Odkryli je pitagorejczycy, ale pewne ogólne metody znajdowania takich trójek liczb były już znane Babilończykom. Jedna z tabliczek klinowych zawiera 15 trojaczków. Wśród nich są trójki składające się z tak dużych liczb, że nie może być mowy o ich znalezieniu drogą selekcji.

Dół Hipokratesa

Luny Hipokratesa to figury ograniczone łukami dwóch okręgów, a ponadto takie, że wykorzystując promienie i długość wspólnej cięciwy tych okręgów, używając kompasu i linijki, można skonstruować kwadraty o jednakowej wielkości.

Z uogólnienia twierdzenia Pitagorasa na półkola wynika, że ​​suma pól różowych grudek pokazanych na rysunku po lewej stronie jest równa powierzchni niebieskiego trójkąta. Dlatego jeśli weźmiesz trójkąt równoramienny, otrzymasz dwie dziury, których powierzchnia będzie równa połowie powierzchni trójkąta. Próbując rozwiązać problem kwadratury koła (patrz Klasyczne problemy starożytności), starożytny grecki matematyk Hipokrates (V w p.n.e.) znalazł jeszcze kilka dziur, których obszary wyrażono w postaci obszarów figur prostoliniowych.

Pełną listę lunul hipomarginalnych uzyskano dopiero w XIX-XX wieku. dzięki zastosowaniu metod teorii Galois.

Upewnij się, że podany trójkąt jest trójkątem prostokątnym, ponieważ twierdzenie Pitagorasa ma zastosowanie tylko do trójkątów prostokątnych.

• W trójkątach prostokątnych jeden z trzech kątów ma zawsze 90 stopni.

Kąt prosty w trójkącie prostokątnym jest oznaczony symbolem kwadratu, a nie symbolem krzywej reprezentującej kąty ukośne. Oznacz boki trójkąta.