Które są równomiernie rozmieszczone. Jednostajne i wykładnicze prawa rozkładu ciągłej zmiennej losowej

Za pomocą których symulowanych jest wiele rzeczywistych procesów. Najczęstszym przykładem jest rozkład jazdy transportu publicznego. Załóżmy, że pewien autobus (trolejbus/tramwaj) kursuje co 10 minut, a Ty zatrzymujesz się w losowym momencie. Jakie jest prawdopodobieństwo, że autobus przyjedzie w ciągu 1 minuty? Oczywiście 1/10. Jakie jest prawdopodobieństwo, że będziesz musiał poczekać 4–5 minut? To samo . Jakie jest prawdopodobieństwo, że będziesz musiał czekać na autobus dłużej niż 9 minut? Jedna dziesiąta!

Rozważmy kilka skończony przedział, niech dla określoności będzie to odcinek. Jeśli zmienna losowa ma stały gęstość rozkładu prawdopodobieństwa na danym segmencie i zerową gęstość poza nim, to mówią, że jest rozłożona równomiernie. W tym przypadku funkcja gęstości będzie ściśle określona:

Rzeczywiście, jeśli długość odcinka (patrz rysunek) jest , wówczas wartość jest nieuchronnie równa - w ten sposób uzyskuje się jednostkę powierzchni prostokąta i obserwuje się ją znana własność:


Sprawdźmy to formalnie:
itp. Z probabilistycznego punktu widzenia oznacza to, że zmienna losowa niezawodnie przyjmę jedną z wartości segmentu..., eh, powoli robię się nudnym starcem =)

Istotą jednolitości jest to, że jakakolwiek wewnętrzna luka stała długość nie rozważaliśmy (pamiętaj o minutach „autobusowych”)– prawdopodobieństwo, że zmienna losowa przyjmie wartość z tego przedziału będzie takie samo. Na rysunku zacieniowałem trzy takie prawdopodobieństwa – jeszcze raz to podkreślam są one określone przez obszary, a nie wartości funkcji!

Rozważmy typowe zadanie:

Przykład 1

Ciągła zmienna losowa jest określona przez jej gęstość rozkładu:

Znajdź stałą, oblicz i utwórz dystrybuantę. Twórz wykresy. Znajdować

Słowem wszystko o czym można marzyć :)

Rozwiązanie: od w przerwie (skończony interwał) , wówczas zmienna losowa ma rozkład równomierny, a wartość „ce” można znaleźć za pomocą wzoru bezpośredniego . Ale ogólnie jest lepiej - używając właściwości:

...dlaczego jest lepiej? Żeby nie było zbędnych pytań ;)

Zatem funkcja gęstości wynosi:

Zróbmy rysunek. Wartości niemożliwe , dlatego też poniżej umieszczono pogrubione kropki:


Dla szybkiego sprawdzenia obliczmy pole prostokąta:
itp.

Znajdźmy oczekiwanie matematyczne i prawdopodobnie już się domyślasz, ile to jest równe. Pamiętaj o autobusie „10-minutowym”: jeśli losowo więc zbliżamy się do przystanku przez wiele, wiele dni średnio będziesz musiał na niego poczekać 5 minut.

Tak, zgadza się - oczekiwanie powinno znajdować się dokładnie w środku przedziału „zdarzenia”:
zgodnie z oczekiwaniami.

Obliczmy wariancję za pomocą formuła . I tutaj potrzebujesz oka i oka przy obliczaniu całki:

Zatem, dyspersja:

Komponujmy funkcja dystrybucji . Nie ma tu nic nowego:

1) jeśli , to i ;

2) jeśli , to i:

3) i wreszcie, kiedy , Dlatego:

W rezultacie:

Zróbmy rysunek:


W przedziale „na żywo” funkcja dystrybucji rozwój liniowy, a to kolejny znak, że mamy zmienną losową o rozkładzie równomiernie rozłożonym. No cóż, oczywiście, po wszystkim pochodna funkcja liniowa- istnieje stała.

Wymagane prawdopodobieństwo można obliczyć na dwa sposoby, korzystając ze znalezionej funkcji rozkładu:

lub używając pewnej całki gęstości:

Ktokolwiek to lubi.

I tu też możesz pisać odpowiedź: ,
, wykresy są wykreślane wzdłuż ścieżki rozwiązania.

… „można”, bo za jego brak zazwyczaj nie ma kary. Zazwyczaj;)

Istnieją specjalne wzory na obliczenie jednolitej zmiennej losowej, które sugeruję wyprowadzić samodzielnie:

Przykład 2

Ciągła zmienna losowa jest dana przez gęstość .

Oblicz matematyczne oczekiwanie i wariancję. Uprość wyniki tak bardzo, jak to możliwe (skrócone wzory na mnożenie pomóc).

Powstałe formuły są wygodne w użyciu do weryfikacji; w szczególności sprawdź właśnie rozwiązany problem, podstawiając do nich określone wartości „a” i „b”. Krótkie rozwiązanie na dole strony.

Na koniec lekcji przyjrzymy się kilku problemom „tekstowym”:

Przykład 3

Wartość podziału skali urządzenia pomiarowego wynosi 0,2. Odczyty przyrządów są zaokrąglane do najbliższej pełnej części. Zakładając, że błędy zaokrągleń rozkładają się równomiernie, znajdź prawdopodobieństwo, że przy następnym pomiarze nie będzie ono większe niż 0,04.

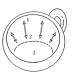
Dla lepszego zrozumienia rozwiązania Wyobraźmy sobie, że jest to jakieś urządzenie mechaniczne ze strzałką, na przykład waga z podziałką 0,2 kg i mamy zważyć świnię w worku. Ale nie po to, aby dowiedzieć się o jego otyłości - teraz ważne będzie GDZIE strzałka zatrzyma się między dwiema sąsiadującymi ze sobą dywizjami.

Rozważmy zmienną losową - dystans strzałki z najbliższy lewicowy podział. Lub od najbliższego po prawej stronie, nie ma to znaczenia.

Utwórzmy funkcję gęstości prawdopodobieństwa:

1) Ponieważ odległość nie może być ujemna, to na przedziale . Logiczny.

2) Z warunku wynika, że ​​strzałka wagi z równe prawdopodobieństwo może zatrzymać się w dowolnym miejscu pomiędzy podziałami * , łącznie z samymi podziałami, a zatem na przedziale:

* Jest to warunek niezbędny. Zatem np. przy ważeniu kawałków waty czy kilogramowych opakowań soli jednorodność zostanie zachowana w znacznie węższych odstępach czasu.

3) A ponieważ odległość od NAJBLIŻSZEGO lewego podziału nie może być większa niż 0,2, to at jest również równe zero.

Zatem:

Warto zaznaczyć, że nikt nas nie pytał o funkcję gęstości, a jej pełną konstrukcję przedstawiłem wyłącznie w łańcuchach poznawczych. Po zakończeniu zadania wystarczy zapisać tylko punkt 2.

Teraz odpowiedzmy na pytanie o problem. Kiedy błąd zaokrąglenia do najbliższego dzielenia nie przekroczy 0,04? Stanie się tak, gdy strzałka zatrzyma się nie dalej niż 0,04 od lewego podziału Prawidłowy Lub nie dalej niż 0,04 od prawego podziału lewy. Na rysunku zacieniowałem odpowiednie obszary:

Pozostaje znaleźć te obszary za pomocą całek. W zasadzie można je policzyć „po szkole” (jak pola prostokątów), ale prostota nie zawsze jest zrozumiała ;)

Przez twierdzenie o dodawaniu prawdopodobieństw zdarzeń niezgodnych:

– prawdopodobieństwo, że błąd zaokrąglenia nie przekroczy 0,04 (w naszym przykładzie 40 gramów)

Łatwo zauważyć, że maksymalny możliwy błąd zaokrąglenia wynosi 0,1 (100 gramów) i dlatego prawdopodobieństwo, że błąd zaokrąglenia nie przekroczy 0,1 równy jeden.

Odpowiedź: 0,4

Istnieją alternatywne wyjaśnienia/sformułowania tego problemu w innych źródłach informacji, ja wybrałem opcję, która wydała mi się najbardziej zrozumiała. Szczególna uwaga należy zwrócić uwagę na fakt, że w stanie możemy mówić o błędach NIE zaokrąglaniu, ale o losowy błędy pomiarowe, które zwykle są (ale nie zawsze), rozłożone normalne prawo. Zatem, Tylko jedno słowo może radykalnie zmienić Twoją decyzję! Bądź czujny i zrozum znaczenie.

I gdy tylko wszystko zatacza koło, nasze stopy prowadzą nas na ten sam przystanek autobusowy:

Przykład 4

Autobusy na danej trasie kursują ściśle według rozkładu i co 7 minut. Utwórz funkcję gęstości zmiennej losowej - czasu oczekiwania na kolejny autobus pasażera, który losowo zbliżył się do przystanku. Znajdź prawdopodobieństwo, że będzie czekał na autobus nie dłużej niż trzy minuty. Znajdź funkcję rozkładu i wyjaśnij jej znaczenie.

Jako przykład ciągłej zmiennej losowej rozważ zmienną losową X równomiernie rozłożoną w przedziale (a; b). Mówi się, że zmienna losowa X jest równomiernie rozłożone na przedziale (a; b), jeżeli gęstość jego rozkładu w tym przedziale nie jest stała:

Z warunku normalizacji wyznaczamy wartość stałej c. Pole pod krzywą gęstości rozkładu powinno być równe jedności, ale w naszym przypadku jest to pole prostokąta o podstawie (b - α) i wysokości c (ryc. 1).

Ryż. 1 Jednolita gęstość dystrybucji
Stąd znajdujemy wartość stałej c:

Zatem gęstość równomiernie rozłożonej zmiennej losowej jest równa

Znajdźmy teraz funkcję rozkładu, korzystając ze wzoru:
1) za
2) za
3) dla 0+1+0=1.
Zatem,

Funkcja rozkładu jest ciągła i nie maleje (ryc. 2).

Ryż. 2 Funkcja rozkładu zmiennej losowej o rozkładzie jednostajnym

Znajdziemy matematyczne oczekiwanie równomiernie rozłożonej zmiennej losowej według wzoru:

Rozproszenie rozkładu równomiernego oblicza się według wzoru i równa się

Przykład nr 1. Wartość podziału skali urządzenia pomiarowego wynosi 0,2. Odczyty przyrządów są zaokrąglane do najbliższej pełnej części. Znajdź prawdopodobieństwo, że podczas liczenia zostanie popełniony błąd: a) mniejsze niż 0,04; b) duży 0,02
Rozwiązanie. Błąd zaokrąglenia jest zmienną losową równomiernie rozłożoną w przedziale pomiędzy sąsiednimi podziałami całkowitymi. Rozważmy przedział (0; 0,2) jako taki podział (ryc. a). Zaokrąglanie można przeprowadzić zarówno w kierunku lewej granicy - 0, jak i w prawo - 0,2, co oznacza, że ​​można popełnić dwukrotnie błąd mniejszy lub równy 0,04, co należy uwzględnić przy obliczaniu prawdopodobieństwa:



P = 0,2 + 0,2 = 0,4

W drugim przypadku wartość błędu może również przekraczać 0,02 na obu granicach podziału, czyli może być większa niż 0,02 lub mniejsza niż 0,18.


Następnie prawdopodobieństwo wystąpienia takiego błędu:

Przykład nr 2. Założono, że stabilność sytuacji gospodarczej w kraju (brak wojen, klęsk żywiołowych itp.) w ciągu ostatnich 50 lat można ocenić na podstawie charakteru rozmieszczenia ludności według wieku: w spokojnej sytuacji należy mundur. W wyniku badania uzyskano dla jednego z krajów następujące dane.

Czy są podstawy sądzić, że w kraju panowała niestabilność?

Rozwiązanie przeprowadzamy za pomocą kalkulatora. Testowanie hipotez. Tabela do obliczania wskaźników.

Grupy	Środek przedziału, x i	Ilość, tj	x i * f ja	Skumulowana częstotliwość, S	|x - x średnia |*f	(x - x śr.) 2 *f	Częstotliwość, f i /n
0 - 10	5	0.14	0.7	0.14	5.32	202.16	0.14
10 - 20	15	0.09	1.35	0.23	2.52	70.56	0.09
20 - 30	25	0.1	2.5	0.33	1.8	32.4	0.1
30 - 40	35	0.08	2.8	0.41	0.64	5.12	0.08
40 - 50	45	0.16	7.2	0.57	0.32	0.64	0.16
50 - 60	55	0.13	7.15	0.7	1.56	18.72	0.13
60 - 70	65	0.12	7.8	0.82	2.64	58.08	0.12
70 - 80	75	0.18	13.5	1	5.76	184.32	0.18
		1	43		20.56	572	1

Wskaźniki centrów dystrybucji.
Średnia ważona


Wskaźniki zmienności.
Absolutne różnice.
Zakres zmienności to różnica między wartościami maksymalnymi i minimalnymi charakterystyki szeregu pierwotnego.
R = X maks. - X min
R = 70 - 0 = 70
Dyspersja- charakteryzuje miarę rozproszenia wokół jej wartości średniej (miara rozproszenia, czyli odchylenia od średniej).


Odchylenie standardowe.

Każda wartość szeregu różni się od średniej wartości 43 nie więcej niż o 23,92
Testowanie hipotez dotyczących rodzaju rozkładu.
4. Testowanie hipotezy dot równomierny rozkład ogólna populacja.
Aby przetestować hipotezę o równomiernym rozkładzie X, tj. zgodnie z prawem: f(x) = 1/(b-a) w przedziale (a,b)
niezbędny:
1. Oszacuj parametry a i b - końce przedziału, w którym zaobserwowano możliwe wartości X, korzystając ze wzorów (znak * oznacza oszacowania parametrów):

2. Znajdź gęstość prawdopodobieństwa oczekiwanego rozkładu f(x) = 1/(b * - a *)
3. Znajdź częstotliwości teoretyczne:
n 1 = nP 1 = n = n*1/(b * - a *)*(x 1 - a *)
n 2 = n 3 = ... = n s-1 = n*1/(b * - a *)*(x i - x i-1)
n s = n*1/(b * - a *)*(b * - x s-1)
4. Porównać częstotliwości empiryczne i teoretyczne, stosując kryterium Pearsona, przyjmując liczbę stopni swobody k = s-3, gdzie s jest liczbą początkowych interwałów próbkowania; jeżeli przeprowadzono kombinację małych częstotliwości, a co za tym idzie samych przedziałów, to s jest liczbą przedziałów pozostałych po kombinacji.

Rozwiązanie:
1. Znajdź oszacowania parametrów a* ib* rozkładu jednostajnego korzystając ze wzorów:


2. Znajdź gęstość założonego rozkładu równomiernego:
f(x) = 1/(b * - a *) = 1/(84,42 - 1,58) = 0,0121
3. Znajdźmy częstotliwości teoretyczne:
n 1 = n*f(x)(x 1 - a *) = 1 * 0,0121(10-1,58) = 0,1
n 8 = n*f(x)(b * - x 7) = 1 * 0,0121(84,42-70) = 0,17
Pozostałe n s będą równe:
n s = n*f(x)(x i - x i-1)

I	n ja	nie*ja	n ja - n * i	(n ja - n* i) 2	(n i - n * i) 2 /n * i
1	0.14	0.1	0.0383	0.00147	0.0144
2	0.09	0.12	-0.0307	0.000943	0.00781
3	0.1	0.12	-0.0207	0.000429	0.00355
4	0.08	0.12	-0.0407	0.00166	0.0137
5	0.16	0.12	0.0393	0.00154	0.0128
6	0.13	0.12	0.0093	8.6E-5	0.000716
7	0.12	0.12	-0.000701	0	4.0E-6
8	0.18	0.17	0.00589	3.5E-5	0.000199
Całkowity	1				0.0532

Wyznaczmy granicę obszaru krytycznego. Ponieważ statystyka Pearsona mierzy różnicę między rozkładami empirycznymi i teoretycznymi, im większa jest jej obserwowana wartość Kobs, tym silniejszy jest argument przeciwko hipotezie głównej.
Dlatego region krytyczny dla tych statystyk jest zawsze praworęczny :)