Równanie stycznej do wykresu funkcji

P. Romanow, T. Romanowa,
Magnitogorsk,
Obwód Czelabińska

Równanie stycznej do wykresu funkcji

Artykuł ukazał się przy wsparciu Kompleksu Hotelowego ITAKA+. Podczas pobytu w mieście stoczniowców Siewierodwińsk nie napotkasz problemu ze znalezieniem tymczasowego mieszkania. , na stronie internetowej kompleksu hotelowego „ITHAKA+” http://itakaplus.ru, możesz łatwo i szybko wynająć mieszkanie w mieście na dowolny okres, za dzienną opłatę.

Na obecnym etapie rozwoju edukacji jednym z jej głównych zadań jest kształtowanie osobowości twórczo myślącej. Zdolność twórczą uczniów można rozwijać tylko wtedy, gdy będą oni systematycznie angażowani w podstawy działalności badawczej. Podstawą wykorzystania przez uczniów swoich sił twórczych, zdolności i talentów jest kształtowana pełnoprawna wiedza i umiejętności. W związku z tym problem kształtowania systemu podstawowej wiedzy i umiejętności dla każdego tematu szkolnego kursu matematyki nie jest mały. Jednocześnie pełnoprawne umiejętności powinny być celem dydaktycznym nie poszczególnych zadań, ale ich starannie przemyślanego systemu. W najszerszym znaczeniu system jest rozumiany jako zbiór wzajemnie powiązanych, oddziałujących na siebie elementów, które charakteryzują się integralnością i stabilną strukturą.

Rozważmy technikę nauczania uczniów, jak napisać równanie stycznej do wykresu funkcji. Zasadniczo wszystkie problemy ze znalezieniem równania stycznego sprowadzają się do konieczności wybrania ze zbioru (wiązki, rodziny) prostych tych, które spełniają określony warunek - są styczne do wykresu określonej funkcji. W takim przypadku zbiór linii, z których dokonywana jest selekcja, można określić na dwa sposoby:

a) punkt leżący na płaszczyźnie xOy (środkowy ołówek linii);
b) współczynnik kątowy (równoległa wiązka linii prostych).

W związku z tym, studiując temat „Styczna do wykresu funkcji” w celu wyodrębnienia elementów układu, zidentyfikowaliśmy dwa rodzaje problemów:

1) problemy dotyczące stycznej danej przez punkt, przez który ona przechodzi;
2) problemy dotyczące stycznej wynikającej z jej nachylenia.

Szkolenie z rozwiązywania problemów stycznych przeprowadzono przy użyciu algorytmu zaproponowanego przez A.G. Mordkowicz. Zasadnicza różnica w stosunku do znanych już polega na tym, że odcięta punktu stycznego jest oznaczona literą a (zamiast x0), w związku z czym równanie stycznej przyjmuje postać

y = f(a) + f "(a)(x – a)

(porównaj z y = f(x 0) + f "(x 0)(x – x 0)). Naszym zdaniem ta technika metodologiczna pozwala uczniom szybko i łatwo zrozumieć, gdzie zapisane są współrzędne bieżącego punktu ogólne równanie styczne i gdzie znajdują się punkty styczności.

Algorytm skomponowania równania stycznego z wykresem funkcji y = f(x)

1. Oznacz odciętą punktu stycznego literą a.
2. Znajdź f(a).
3. Znajdź f „(x) i f” (a).
4. Podstaw znalezione liczby a, f(a), f „(a) do ogólnego równania stycznego y = f(a) = f „(a)(x – a).

Algorytm ten można zestawić na podstawie samodzielnej identyfikacji przez studentów operacji i kolejności ich wykonywania.

Praktyka pokazała, że ​​sekwencyjne rozwiązywanie każdego z kluczowych problemów za pomocą algorytmu pozwala rozwinąć umiejętności zapisywania równania stycznej na wykresie funkcji etapami, a kroki algorytmu służą jako punkty odniesienia dla działań . Podejście to odpowiada teorii stopniowego kształtowania się działań umysłowych opracowanej przez P.Ya. Galperin i N.F. Talyzina.

W pierwszym typie zadań zidentyfikowano dwa zadania kluczowe:

• styczna przechodzi przez punkt leżący na krzywej (zadanie 1);
• styczna przechodzi przez punkt nie leżący na krzywej (zadanie 2).

Zadanie 1. Napisz równanie stycznej do wykresu funkcji w punkcie M(3; – 2).

Rozwiązanie. Punkt M(3; – 2) jest punktem stycznym, ponieważ

1. a = 3 – odcięta punktu stycznego.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – równanie styczne.

Zadanie 2. Zapisz równania wszystkich stycznych do wykresu funkcji y = – x 2 – 4x + 2 przechodzącej przez punkt M(– 3; 6).

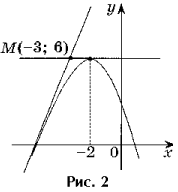Rozwiązanie. Punkt M(– 3; 6) nie jest punktem stycznym, gdyż f(– 3) 6 (ryc. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – równanie styczne.

Styczna przechodzi przez punkt M(– 3; 6), zatem jej współrzędne spełniają równanie styczne.

6 = – za 2 – 4a + 2 – 2(a + 2)(– 3 – a),
za 2 + 6a + 8 = 0^ za 1 = – 4, za 2 = – 2.

Jeśli a = – 4, to równanie styczne ma postać y = 4x + 18.

Jeżeli a = – 2, to równanie styczne ma postać y = 6.

W drugim typie kluczowymi zadaniami będą:

• styczna jest równoległa do jakiejś prostej (zadanie 3);
• styczna przechodzi pod pewnym kątem do danej prostej (zadanie 4).

Zadanie 3. Zapisz równania wszystkich stycznych do wykresu funkcji y = x 3 – 3x 2 + 3, równolegle do prostej y = 9x + 1.

Rozwiązanie.

1. a – odcięta punktu stycznego.
2. f(a) = za 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Ale z drugiej strony f "(a) = 9 (warunek równoległości). Oznacza to, że musimy rozwiązać równanie 3a 2 – 6a = 9. Jego pierwiastki to a = – 1, a = 3 (ryc. 3 ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f „(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – równanie styczne;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – równanie styczne.

Zadanie 4. Zapisz równanie stycznej do wykresu funkcji y = 0,5x 2 – 3x + 1, przechodzącej pod kątem 45° do prostej y = 0 (rys. 4).

Rozwiązanie. Z warunku f "(a) = tan 45° znajdujemy a: a – 3 = 1^a = 4.

1. a = 4 – odcięta punktu stycznego.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – równanie styczne.

Łatwo pokazać, że rozwiązanie dowolnego innego problemu sprowadza się do rozwiązania jednego lub większej liczby problemów kluczowych. Rozważmy jako przykład dwa poniższe problemy.

1. Zapisz równania stycznych do paraboli y = 2x 2 – 5x – 2, jeśli styczne przecinają się pod kątem prostym i jedna z nich dotyka paraboli w punkcie o odciętej 3 (rys. 5).

Rozwiązanie. Ponieważ podana jest odcięta punktu styczności, pierwsza część rozwiązania sprowadza się do kluczowego problemu 1.

1. a = 3 – odcięta punktu styczności jednego z boków kąta prostego.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – równanie pierwszej stycznej.

Niech a – kąt nachylenia pierwszej stycznej. Ponieważ styczne są prostopadłe, to jest kąt nachylenia drugiej stycznej. Z równania y = 7x – 20 pierwszej stycznej mamy tg a = 7. Znajdźmy

Oznacza to, że nachylenie drugiej stycznej jest równe .

Dalsze rozwiązanie sprowadza się do kluczowego zadania 3.

Niech B(c; f(c)) będzie zatem punktem styczności drugiej prostej

1. – odcięta drugiego punktu styczności.
2.
3.
4.
– równanie drugiej stycznej.

Notatka. Współczynnik kątowy stycznej można łatwiej znaleźć, jeśli uczniowie znają stosunek współczynników prostych prostopadłych k 1 k 2 = – 1.

2. Zapisz równania wszystkich wspólnych stycznych do wykresów funkcji

Rozwiązanie. Zadanie sprowadza się do znalezienia odciętej punktów stycznych wspólnych stycznych, czyli rozwiązania kluczowego problemu 1 w postaci ogólnej, ułożenia układu równań i następnie jego rozwiązania (rys. 6).

1. Niech a będzie odciętą punktu stycznego leżącego na wykresie funkcji y = x 2 + x + 1.
2. f(a) = za 2 + za + 1.
3. f "(a) = 2a + 1.
4. y = za 2 + za + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – za 2 .

1. Niech c będzie odciętą punktu stycznego leżącego na wykresie funkcji
2.
3. f "(c) = do.
4.

Zatem styczne są ogólne

Zatem y = x + 1 i y = – 3x – 3 są wspólnymi stycznymi.

Głównym celem rozważanych zadań jest przygotowanie studentów do samodzielnego rozpoznawania rodzaju problemu kluczowego przy rozwiązywaniu bardziej złożonych problemów wymagających określonych umiejętności badawczych (umiejętność analizowania, porównywania, uogólniania, stawiania hipotez itp.). Do takich zadań zalicza się każde zadanie, którego elementem jest zadanie kluczowe. Rozważmy jako przykład problem (odwrotny do Zadania 1) znalezienia funkcji z rodziny jej stycznych.

3. Dla jakich b i c proste y = x i y = – 2x są styczne do wykresu funkcji y = x 2 + bx + c?

Rozwiązanie.

Niech t będzie odciętą punktu styczności prostej y = x z parabolą y = x 2 + bx + c; p jest odciętą punktu styczności prostej y = – 2x z parabolą y = x 2 + bx + c. Wtedy równanie styczne y = x przyjmie postać y = (2t + b)x + c – t 2 , a równanie styczne y = – 2x przyjmie postać y = (2p + b)x + c – p 2 .

Ułóżmy i rozwiążmy układ równań

Odpowiedź:

Problemy do samodzielnego rozwiązania

1. Zapisz równania stycznych do wykresu funkcji y = 2x 2 – 4x + 3 w punktach przecięcia wykresu z prostą y = x + 3.

Odpowiedź: y = – 4x + 3, y = 6x – 9,5.

2. Dla jakich wartości a tangens poprowadzony do wykresu funkcji y = x 2 – ax w punkcie wykresu z odciętą x 0 = 1 przechodzi przez punkt M(2; 3)?

Odpowiedź: a = 0,5.

3. Dla jakich wartości p prosta y = px – 5 styka się z krzywą y = 3x 2 – 4x – 2?

Odpowiedź: p 1 = – 10, p 2 = 2.

4. Znajdź wszystkie punkty wspólne wykresu funkcji y = 3x – x 3 oraz styczną do tego wykresu poprowadzoną przez punkt P(0; 16).

Odpowiedź: A(2; – 2), B(– 4; 52).

5. Znajdź najkrótszą odległość między parabolą y = x 2 + 6x + 10 a prostą

Odpowiedź:

6. Znajdź na krzywej y = x 2 – x + 1 punkt, w którym styczna do wykresu jest równoległa do prostej y – 3x + 1 = 0.

Odpowiedź: M(2; 3).

7. Zapisz równanie stycznej do wykresu funkcji y = x 2 + 2x – | 4x |, który dotyka go w dwóch punktach. Narysuj coś.

Odpowiedź: y = 2x – 4.

8. Udowodnij, że prosta y = 2x – 1 nie przecina krzywej y = x 4 + 3x 2 + 2x. Znajdź odległość pomiędzy ich najbliższymi punktami.

Odpowiedź:

9. Na paraboli y = x 2 wyznacza się dwa punkty za pomocą odciętych x 1 = 1, x 2 = 3. Przez te punkty rysuje się sieczną. W którym punkcie paraboli styczna do niej będzie równoległa do siecznej? Zapisz równania siecznej i stycznej.

Odpowiedź: y = 4x – 3 – równanie sieczne; y = 4x – 4 – równanie styczne.

10. Znajdź kąt q pomiędzy stycznymi do wykresu funkcji y = x 3 – 4x 2 + 3x + 1, narysowanymi w punktach o odciętych 0 i 1.

Odpowiedź: q = 45°.

11. W jakich punktach styczna do wykresu funkcji tworzy z osią Ox kąt 135°?

Odpowiedź: A(0; – 1), B(4; 3).

12. W punkcie A(1; 8) do krzywej rysowana jest styczna. Znajdź długość odcinka stycznego pomiędzy osiami współrzędnych.

Odpowiedź:

13. Zapisz równanie wszystkich wspólnych stycznych do wykresów funkcji y = x 2 – x + 1 i y = 2x 2 – x + 0,5.

Odpowiedź: y = – 3x i y = x.

14. Znajdź odległość stycznych do wykresu funkcji równolegle do osi x.

Odpowiedź:

15. Określ, pod jakim kątem parabola y = x 2 + 2x – 8 przecina oś x.

Odpowiedź: q 1 = arctan 6, q 2 = arctan (– 6).

16. Wykres funkcji znajdź wszystkie punkty, z których styczna do tego wykresu przecina dodatnie półosie współrzędnych, odcinając od nich równe odcinki.

Odpowiedź: A(– 3; 11).

17. Prosta y = 2x + 7 i parabola y = x 2 – 1 przecinają się w punktach M i N. Znajdź punkt K przecięcia prostych stycznych do paraboli w punktach M i N.

Odpowiedź: K(1; – 9).

18. Dla jakich wartości b prosta y = 9x + b jest styczna do wykresu funkcji y = x 3 – 3x + 15?

Odpowiedź 1; 31.

19. Dla jakich wartości k prosta y = kx – 10 ma tylko jeden punkt wspólny z wykresem funkcji y = 2x 2 + 3x – 2? Dla znalezionych wartości k określ współrzędne punktu.

Odpowiedź: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).

20. Dla jakich wartości b tangens poprowadzony do wykresu funkcji y = bx 3 – 2x 2 – 4 w punkcie z odciętą x 0 = 2 przechodzi przez punkt M(1; 8)?

Odpowiedź: b = – 3.

21. Parabola z wierzchołkiem na osi Wół dotyka prostej przechodzącej przez punkty A(1; 2) i B(2; 4) w punkcie B. Znajdź równanie paraboli.

Odpowiedź:

22. Przy jakiej wartości współczynnika k parabola y = x 2 + kx + 1 styka się z osią Wółu?

Odpowiedź: k = d 2.

23. Znajdź kąty pomiędzy prostą y = x + 2 i krzywą y = 2x 2 + 4x – 3.

29. Znajdź odległość stycznych do wykresu funkcji i generatorów o dodatnim kierunku osi Ox pod kątem 45°.

Odpowiedź:

30. Znajdź miejsce wierzchołków wszystkich paraboli postaci y = x 2 + ax + b styczne do prostej y = 4x – 1.

Odpowiedź: linia prosta y = 4x + 3.

Literatura

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra i początki analizy: 3600 problemów uczniów i rozpoczynających naukę na uniwersytetach. – M., Drop, 1999.
2. Mordkovich A. Seminarium czwarte dla młodych nauczycieli. Temat: Aplikacje pochodne. – M., „Matematyka”, nr 21/94.
3. Kształcenie wiedzy i umiejętności w oparciu o teorię stopniowego przyswajania działań umysłowych. / wyd. P.Ya. Galperina, NF Talyzina. – M., Moskiewski Uniwersytet Państwowy, 1968.

W artykule szczegółowo wyjaśniono definicje, znaczenie geometryczne pochodnej wraz z oznaczeniami graficznymi. Równanie stycznej zostanie omówione na przykładach, znalezione zostaną równania stycznej do krzywych drugiego rzędu.

Yandex.RTB R-A-339285-1 Definicja 1

Kąt nachylenia prostej y = k x + b nazywany jest kątem α i mierzonym od dodatniego kierunku osi x do prostej y = k x + b w kierunku dodatnim.

Na rysunku kierunek x jest oznaczony zieloną strzałką i zielonym łukiem, a kąt nachylenia czerwonym łukiem. Niebieska linia odnosi się do linii prostej.

Definicja 2

Nachylenie prostej y = k x + b nazywa się współczynnikiem liczbowym k.

Współczynnik kątowy jest równy tangensowi prostej, czyli k = t g α.

• Kąt nachylenia prostej jest równy 0 tylko wtedy, gdy jest równoległa względem x, a nachylenie jest równe zero, ponieważ tangens zera jest równy 0. Oznacza to, że równanie będzie miało postać y = b.
• Jeżeli kąt nachylenia prostej y = k x + b jest ostry, to warunek 0 jest spełniony< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, a na wykresie następuje wzrost.
• Jeśli α = π 2, to położenie prostej jest prostopadłe do x. Równość jest określona przez x = c, gdzie wartość c jest liczbą rzeczywistą.
• Jeżeli kąt nachylenia prostej y = k x + b jest rozwarty, to odpowiada warunkom π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definicja 3

Sieczna to prosta przechodząca przez 2 punkty funkcji f (x). Innymi słowy, sieczna to linia prosta poprowadzona przez dowolne dwa punkty na wykresie danej funkcji.

Rysunek pokazuje, że AB jest sieczną, a f (x) jest czarną krzywą, α jest czerwonym łukiem, wskazującym kąt nachylenia siecznej.

Kiedy współczynnik kątowy linii prostej jest równy tangensowi kąta nachylenia, jasne jest, że tangens trójkąta prostokątnego A B C można znaleźć poprzez stosunek przeciwnej strony do sąsiedniej.

Definicja 4

Otrzymujemy wzór na znalezienie secansu postaci:

k = t g α = B C A C = f (x B) - f x A x B - x A, gdzie odcięte punktów A i B są wartościami x A, x B i f (x A), f (x B) są funkcjami wartości w tych punktach.

Oczywiście współczynnik kątowy siecznej wyznacza się za pomocą równości k = f (x B) - f (x A) x B - x A lub k = f (x A) - f (x B) x A - x B , a równanie należy zapisać jako y = f (x B) - f (x A) x B - x A x - x A + f (x A) lub
y = fa (x ZA) - fa (x B) x A - x B x - x B + fa (x B) .

Sieczna dzieli wykres wizualnie na 3 części: na lewo od punktu A, od A do B, na prawo od B. Poniższy rysunek pokazuje, że istnieją trzy sieczne, które są uważane za zbieżne, to znaczy są ustalane za pomocą podobne równanie.

Z definicji jasne jest, że linia prosta i jej sieczna w tym przypadku pokrywają się.

Sieczna może przecinać wykres danej funkcji wielokrotnie. Jeżeli dla siecznej istnieje równanie w postaci y = 0, to liczba punktów przecięcia z sinusoidą jest nieskończona.

Definicja 5

Styczna do wykresu funkcji f (x) w punkcie x 0 ; f (x 0) jest linią prostą przechodzącą przez dany punkt x 0; f (x 0), z obecnością segmentu, który ma wiele wartości x bliskich x 0.

Przykład 1

Przyjrzyjmy się bliżej poniższemu przykładowi. Wtedy widać, że prostą wyznaczoną funkcją y = x + 1 uważa się za styczną do y = 2 x w punkcie o współrzędnych (1; 2). Dla jasności należy wziąć pod uwagę wykresy o wartościach bliskich (1; 2). Funkcja y = 2 x jest zaznaczona kolorem czarnym, niebieska linia to styczna, a czerwona kropka to punkt przecięcia.

Oczywiście y = 2 x łączy się z linią y = x + 1.

Aby wyznaczyć styczną, powinniśmy rozważyć zachowanie stycznej A B, gdy punkt B zbliża się do punktu A w nieskończoność. Dla przejrzystości przedstawiamy rysunek.

Sieczna A B, oznaczona niebieską linią, zmierza do położenia samej stycznej, a kąt nachylenia siecznej α zacznie zmierzać do kąta nachylenia samej stycznej α x.

Definicja 6

Styczną do wykresu funkcji y = f (x) w punkcie A uważa się za położenie graniczne siecznej A B, ponieważ B dąży do A, czyli B → A.

Przejdźmy teraz do rozważenia geometrycznego znaczenia pochodnej funkcji w punkcie.

Przejdźmy dalej do rozważenia siecznej A B dla funkcji f (x), gdzie A i B o współrzędnych x 0, f (x 0) i x 0 + ∆ x, f (x 0 + ∆ x), i ∆ x wynoszą oznaczane jako przyrost argumentu. Teraz funkcja przyjmie postać ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Dla jasności podamy przykład rysunku.

Rozważ powstały trójkąt prostokątny A B C. Do rozwiązania używamy definicji stycznej, czyli otrzymujemy relację ∆ y ∆ x = t g α . Z definicji stycznej wynika, że ​​lim ∆ x → 0 ∆ y ∆ x = t g α x . Zgodnie z zasadą pochodnej w punkcie mamy, że pochodna f (x) w punkcie x 0 nazywana jest granicą stosunku przyrostu funkcji do przyrostu argumentu, gdzie ∆ x → 0 , oznaczamy to jako f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Wynika z tego, że f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, gdzie k x oznacza się jako nachylenie stycznej.

Oznacza to, że stwierdzamy, że f ' (x) może istnieć w punkcie x 0 i podobnie jak styczna do danego wykresu funkcji w punkcie styczności równej x 0, f 0 (x 0), gdzie wartość nachylenie stycznej w punkcie jest równe pochodnej w punkcie x 0 . Wtedy otrzymujemy, że k x = f " (x 0) .

Znaczenie geometryczne pochodnej funkcji w punkcie polega na tym, że daje ona pojęcie o istnieniu stycznej do wykresu w tym samym punkcie.

Aby zapisać równanie dowolnej linii prostej na płaszczyźnie, konieczne jest posiadanie współczynnika kątowego z punktem, przez który ona przechodzi. Przyjmuje się, że jego zapis wynosi x 0 na przecięciu.

Równanie styczne do wykresu funkcji y = f (x) w punkcie x 0, f 0 (x 0) przyjmuje postać y = f "(x 0) x - x 0 + f (x 0).

Oznacza to, że ostateczna wartość pochodnej f "(x 0) może określić położenie stycznej, czyli w pionie, pod warunkiem, że lim x → x 0 + 0 f " (x) = ∞ i lim x → x 0 - 0 fa "(x ) = ∞ lub w ogóle nieobecny pod warunkiem lim x → x 0 + 0 fa " (x) ≠ lim x → x 0 - 0 fa " (x) .

Położenie stycznej zależy od wartości jej współczynnika kątowego k x = f "(x 0). Gdy równolegle do osi o x otrzymujemy, że k k = 0, gdy równolegle do około y - k x = ∞, oraz postać równanie styczne x = x 0 rośnie wraz z k x > 0, maleje wraz z k x< 0 .

Przykład 2

Ułóż równanie stycznej do wykresu funkcji y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 w punkcie o współrzędnych (1; 3) i wyznacz kąt nachylenia.

Rozwiązanie

Pod warunkiem mamy, że funkcja jest zdefiniowana dla wszystkich liczb rzeczywistych. Stwierdzamy, że punkt o współrzędnych określonych warunkiem (1; 3) jest punktem styczności, wówczas x 0 = - 1, f (x 0) = - 3.

Należy znaleźć pochodną w punkcie o wartości - 1. Rozumiemy to

y " = mi x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = mi x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = mi x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = mi - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Wartość f' (x) w punkcie styczności jest nachyleniem stycznej, która jest równa stycznej nachylenia.

Następnie k x = t g α x = y " (x 0) = 3 3

Wynika z tego, że α x = a r do t sol 3 3 = π 6

Odpowiedź: równanie styczne przyjmuje postać

y = fa " (x 0) x - x 0 + fa (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Dla przejrzystości podajemy przykład na ilustracji graficznej.

Kolorem czarnym oznaczono wykres oryginalnej funkcji, kolor niebieski przedstawia styczną, a czerwona kropka oznacza punkt styczności. Rysunek po prawej stronie przedstawia widok w powiększeniu.

Przykład 3

Ustalić istnienie stycznej do wykresu danej funkcji
y = 3 · x - 1 5 + 1 w punkcie o współrzędnych (1 ; 1) . Napisz równanie i określ kąt nachylenia.

Rozwiązanie

Pod warunkiem mamy, że za dziedzinę definicji danej funkcji uważa się zbiór wszystkich liczb rzeczywistych.

Przejdźmy do znalezienia pochodnej

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Jeśli x 0 = 1, to f' (x) jest nieokreślone, ale granice są zapisywane jako lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ i lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞, co oznacza istnienie stycznej pionowej w punkcie (1; 1).

Odpowiedź: równanie przyjmie postać x = 1, gdzie kąt nachylenia będzie równy π 2.

Dla jasności przedstawmy to graficznie.

Przykład 4

Znajdź punkty na wykresie funkcji y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, gdzie

1. Nie ma stycznej;
2. Styczna jest równoległa do x;
3. Styczna jest równoległa do prostej y = 8 5 x + 4.

Rozwiązanie

Należy zwrócić uwagę na zakres definicji. Pod warunkiem mamy, że funkcja jest zdefiniowana na zbiorze wszystkich liczb rzeczywistych. Rozbudowujemy moduł i rozwiązujemy układ o przedziałach x ∈ - ∞ ; 2 i [- 2; + ∞) . Rozumiemy to

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Konieczne jest różniczkowanie funkcji. Mamy to

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Gdy x = − 2, to pochodna nie istnieje, ponieważ jednostronne granice nie są w tym punkcie równe:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Obliczamy wartość funkcji w punkcie x = - 2, gdzie to otrzymujemy

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, czyli styczna w punkcie ( - 2; - 2) nie będzie istnieć.
2. Styczna jest równoległa do x, gdy nachylenie wynosi zero. Następnie k x = t g α x = f "(x 0). Oznacza to, że konieczne jest znalezienie wartości takiego x, gdy pochodna funkcji zamienia ją na zero. To znaczy wartości f ' (x) będą punktami styczności, gdzie styczna jest równoległa do x .

Kiedy x ∈ - ∞ ; - 2, wówczas - 1 5 (x 2 + 12 x + 35) = 0, a dla x ∈ (- 2; + ∞) otrzymujemy 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 re = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 re = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Oblicz odpowiednie wartości funkcji

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Stąd - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 są uważane za wymagane punkty wykresu funkcji.

Spójrzmy na graficzną reprezentację rozwiązania.

Czarna linia to wykres funkcji, czerwone kropki to punkty styczności.

1. Gdy linie są równoległe, współczynniki kątowe są równe. Następnie należy wyszukać punkty na wykresie funkcji, w których nachylenie będzie równe wartości 8 5. Aby to zrobić, musisz rozwiązać równanie postaci y "(x) = 8 5. Następnie, jeśli x ∈ - ∞; - 2, otrzymujemy to - 1 5 (x 2 + 12 x + 35) = 8 5, a jeśli x ∈ ( - 2 ; + ∞), to 1 5 (x 2 - 4 x + 3) = 8 5.

Pierwsze równanie nie ma pierwiastków, ponieważ dyskryminator jest mniejszy od zera. Zapiszmy to

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Zatem inne równanie ma dwa rzeczywiste pierwiastki

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 re = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Przejdźmy do znalezienia wartości funkcji. Rozumiemy to

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Punkty o wartościach - 1; 4 15, 5; 8 3 to punkty, w których styczne są równoległe do prostej y = 8 5 x + 4.

Odpowiedź: linia czarna – wykres funkcji, linia czerwona – wykres y = 8 5 x + 4, linia niebieska – styczne w punktach - 1; 4 15, 5; 8 3.

Dla danych funkcji może istnieć nieskończona liczba tangensów.

Przykład 5

Zapisz równania wszystkich dostępnych stycznych funkcji y = 3 cos 3 2 x - π 4 - 1 3, które leżą prostopadle do prostej y = - 2 x + 1 2.

Rozwiązanie

Aby skompilować równanie styczne, należy znaleźć współczynnik i współrzędne punktu stycznego, w oparciu o warunek prostopadłości linii. Definicja jest następująca: iloczyn współczynników kątowych prostopadłych do prostych jest równy -1, czyli zapisywany jako k x · k ⊥ = - 1. Z warunku mamy, że współczynnik kątowy leży prostopadle do prostej i jest równy k ⊥ = - 2, wówczas k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Teraz musisz znaleźć współrzędne punktów dotyku. Musisz znaleźć x, a następnie jego wartość dla danej funkcji. Należy zauważyć, że z geometrycznego znaczenia pochodnej w punkcie
x 0 otrzymujemy, że k x = y "(x 0). Z tej równości znajdujemy wartości x dla punktów styku.

Rozumiemy to

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - grzech 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 grzech 3 2 x 0 - π 4 3 2 = - 9 2 grzech 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 grzech 3 2 x 0 - π 4 = 1 2 ⇒ grzech 3 2 x 0 - π 4 = - 1 9

To równanie trygonometryczne zostanie użyte do obliczenia rzędnych punktów stycznych.

3 2 x 0 - π 4 = a r do sin - 1 9 + 2 πk lub 3 2 x 0 - π 4 = π - a r do grzech - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r do sin 1 9 + 2 πk lub 3 2 x 0 - π 4 = π + za r do sin 1 9 + 2 πk

x 0 = 2 3 π 4 - za r do sin 1 9 + 2 πk lub x 0 = 2 3 5 π 4 + za r do sin 1 9 + 2 πk , k ∈ Z

Z jest zbiorem liczb całkowitych.

znaleziono x punktów kontaktowych. Teraz musisz przejść do wyszukiwania wartości y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - grzech 2 3 2 x 0 - π 4 - 1 3 lub y 0 = 3 - 1 - grzech 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 lub y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 lub y 0 = - 4 5 + 1 3

Z tego otrzymujemy, że 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r do grzech 1 9 + 2 πk ; - 4 5 + 1 3 to punkty styczności.

Odpowiedź: niezbędne równania zostaną zapisane jako

y = 1 2 x - 2 3 π 4 - za r do grzech 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + za r do grzech 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Aby uzyskać reprezentację wizualną, rozważ funkcję i styczną na linii współrzędnych.

Z rysunku wynika, że ​​funkcja znajduje się na przedziale [-10; 10 ], gdzie czarna linia to wykres funkcji, niebieskie linie to styczne, które leżą prostopadle do danej prostej postaci y = - 2 x + 1 2. Czerwone kropki to punkty dotykowe.

Równania kanoniczne krzywych drugiego rzędu nie są funkcjami jednowartościowymi. Równania styczne dla nich są zestawiane według znanych schematów.

Styczna do okręgu

Aby zdefiniować okrąg ze środkiem w punkcie x środek t e r ; y c e n t e r i promień R, zastosuj wzór x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Równość tę można zapisać jako sumę dwóch funkcji:

y = R 2 - x - x do mi n t mi r 2 + y do mi n t e r y = - R 2 - x - x do mi n t mi r 2 + y do mi n t mi r

Pierwsza funkcja znajduje się na górze, a druga na dole, jak pokazano na rysunku.

Aby ułożyć równanie okręgu w punkcie x 0; y 0 , który znajduje się w górnym lub dolnym półkolu, powinieneś znaleźć równanie wykresu funkcji postaci y = R 2 - x - x c e n t e r 2 + y c e n t e r lub y = - R 2 - x - x c e n t e r 2 + centrum we wskazanym punkcie.

Kiedy w punktach x cent e r ; y c e n t e r + R i x c e n t e r ; y c e n t e r - R styczne można wyrazić za pomocą równań y = y c e n t e r + R i y = y c e n t e r - R oraz w punktach x c e n t e r + R ; y centrum i
x środek t e r - R ; y c e n t e r będzie równoległe do o y, wówczas otrzymamy równania postaci x = x c e n t e r + R i x = x c e n t e r - R .

Styczna do elipsy

Gdy elipsa ma środek w xcenter r ; y centrum t e r z półosiami a i b, to można to określić za pomocą równania x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Elipsę i okrąg można oznaczyć poprzez połączenie dwóch funkcji, a mianowicie górnej i dolnej półelipsy. Wtedy to zrozumiemy

y = b za · za 2 - (x - x do e n t mi r) 2 + y do mi n t e r y = - b a · za 2 - (x - x do mi n t e r) 2 + y do mi n t mi r

Jeżeli styczne znajdują się na wierzchołkach elipsy, to są one równoległe względem x lub y. Poniżej, dla jasności, rozważ rysunek.

Przykład 6

Zapisz równanie stycznej do elipsy x - 3 2 4 + y - 5 2 25 = 1 w punktach o wartościach x równych x = 2.

Rozwiązanie

Konieczne jest znalezienie punktów stycznych odpowiadających wartości x = 2. Podstawiamy do istniejącego równania elipsy i znajdujemy to

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Następnie 2; 5 3 2 + 5 i 2; - 5 3 2 + 5 to punkty styczne należące do górnej i dolnej półelipsy.

Przejdźmy do znalezienia i rozwiązania równania elipsy względem y. Rozumiemy to

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Oczywiście górną półelipsę określa się funkcją w postaci y = 5 + 5 2 4 - x - 3 2, a dolną półelipsę y = 5 - 5 2 4 - x - 3 2.

Zastosujmy standardowy algorytm do utworzenia równania stycznej do wykresu funkcji w punkcie. Napiszmy, że równanie dla pierwszej stycznej w punkcie 2; 5 3 2 + 5 będzie wyglądać

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Znajdujemy, że równanie drugiej stycznej z wartością w punkcie
2; - 5 3 2 + 5 przyjmuje formę

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graficznie styczne są oznaczone w następujący sposób:

Styczna do hiperboli

Kiedy hiperbola ma środek w x centrum ; y środek i wierzchołki x środek t e r + α ; y centrum t i x cen t e r - α; y c e n t e r , nierówność x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 ma miejsce, jeśli z wierzchołkami x c e n t e r ; y c e n t e r + b i x c e n t e r ; y c e n t e r - b , wówczas określa się je za pomocą nierówności x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbolę można przedstawić jako dwie połączone funkcje formy

y = b za · (x - x do e n t e r) 2 - za 2 + y do mi n t e r y = - b a · (x - x do mi n t e r) 2 - za 2 + y c e n t e r lub y = b a · (x - x c e n t e r) 2 + za 2 + y do e n t e r y = - b a · (x - x c e n t e r) 2 + za 2 + y c e n t e r

W pierwszym przypadku mamy, że styczne są równoległe do y, a w drugim są równoległe do x.

Wynika z tego, że aby znaleźć równanie stycznej do hiperboli, należy dowiedzieć się, do jakiej funkcji należy punkt styczności. Aby to ustalić, należy podstawić równania i sprawdzić identyczność.

Przykład 7

Napisz równanie stycznej do hiperboli x - 3 2 4 - y + 3 2 9 = 1 w punkcie 7; - 3 3 - 3 .

Rozwiązanie

Konieczne jest przekształcenie zapisu rozwiązania w celu znalezienia hiperboli za pomocą 2 funkcji. Rozumiemy to

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 i y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Należy określić do jakiej funkcji należy dany punkt o współrzędnych 7; - 3 3 - 3 .

Oczywiście do sprawdzenia pierwszej funkcji potrzebne jest y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, wtedy punkt nie należy do wykresu, ponieważ równość nie zachodzi.

Dla drugiej funkcji mamy, że y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, co oznacza, że ​​punkt należy do danego wykresu. Stąd powinieneś znaleźć zbocze.

Rozumiemy to

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Odpowiedź: równanie styczne można przedstawić jako

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Jest to wyraźnie przedstawione w ten sposób:

Styczna do paraboli

Aby utworzyć równanie stycznej do paraboli y = a x 2 + b x + c w punkcie x 0, y (x 0), należy zastosować standardowy algorytm, wówczas równanie przybierze postać y = y ”(x 0) x - x 0 + y ( x 0). Taka styczna w wierzchołku jest równoległa do x.

Powinieneś zdefiniować parabolę x = a y 2 + b y + c jako sumę dwóch funkcji. Dlatego musimy rozwiązać równanie dla y. Rozumiemy to

x = za y 2 + b y + do ⇔ za y 2 + b y + do - x = 0 re = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Graficznie przedstawiony jako:

Aby dowiedzieć się czy punkt x 0, y (x 0) należy do funkcji, postępuj delikatnie według standardowego algorytmu. Taka styczna będzie równoległa do oy względem paraboli.

Przykład 8

Zapisz równanie stycznej do wykresu x - 2 y 2 - 5 y + 3 gdy mamy kąt styczny równy 150°.

Rozwiązanie

Rozwiązanie zaczynamy od przedstawienia paraboli jako dwóch funkcji. Rozumiemy to

2 lata 2 - 5 lat + 3 - x = 0 re = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Wartość nachylenia jest równa wartości pochodnej w punkcie x 0 tej funkcji i jest równa tangensowi kąta nachylenia.

Otrzymujemy:

k x = y "(x 0) = t sol α x = t g 150 ° = - 1 3

Stąd określamy wartość x dla punktów styku.

Pierwsza funkcja zostanie zapisana jako

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Oczywiście nie ma prawdziwych pierwiastków, ponieważ otrzymaliśmy wartość ujemną. Dochodzimy do wniosku, że dla takiej funkcji nie ma stycznej o kącie 150°.

Druga funkcja zostanie zapisana jako

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Mamy, że punktów styku jest 23 4 ; - 5 + 3 4 .

Odpowiedź: równanie styczne przyjmuje postać

y = - 1 3 x - 23 4 + - 5 + 3 4

Przedstawmy to graficznie w ten sposób:

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Ten program matematyczny znajduje równanie stycznej do wykresu funkcji \(f(x)\) w punkcie określonym przez użytkownika \(a\).

Program nie tylko wyświetla równanie styczne, ale także wyświetla proces rozwiązywania problemu.

Ten kalkulator online może być przydatny dla uczniów szkół średnich podczas przygotowań do sprawdzianów i egzaminów, podczas sprawdzania wiedzy przed egzaminem Unified State Exam, a także dla rodziców do kontrolowania rozwiązania wielu problemów z matematyki i algebry. A może wynajęcie korepetytora lub zakup nowych podręczników jest dla Ciebie zbyt kosztowny? A może po prostu chcesz jak najszybciej odrobić zadanie domowe z matematyki lub algebry? W tym przypadku możesz także skorzystać z naszych programów ze szczegółowymi rozwiązaniami.

W ten sposób możesz prowadzić własne szkolenie i/lub szkolenie swoich młodszych braci, a jednocześnie wzrasta poziom edukacji w zakresie rozwiązywania problemów.

Jeśli chcesz znaleźć pochodną funkcji, mamy do tego zadanie Znajdź pochodną.

Jeżeli nie znasz zasad wprowadzania funkcji, polecamy się z nimi zapoznać.

Wprowadź wyrażenie funkcyjne \(f(x)\) i liczbę \(a\)

f(x)=
a=

Znajdź równanie styczne

Odkryto, że niektóre skrypty niezbędne do rozwiązania tego problemu nie zostały załadowane i program może nie działać.
Być może masz włączonego AdBlocka.
W takim przypadku wyłącz ją i odśwież stronę.

JavaScript jest wyłączony w Twojej przeglądarce.
Aby rozwiązanie się pojawiło, musisz włączyć JavaScript.
Poniżej znajdują się instrukcje dotyczące włączania JavaScript w Twojej przeglądarce.

Ponieważ Chętnych do rozwiązania problemu jest wiele, Twoja prośba została umieszczona w kolejce.
Za kilka sekund rozwiązanie pojawi się poniżej.
Proszę czekać sekunda...

Jeśli ty zauważył błąd w rozwiązaniu, możesz napisać o tym w Formularzu opinii.
Nie zapomnij wskaż, które zadanie ty decydujesz co wpisz w pola.

Nasze gry, puzzle, emulatory:

Trochę teorii.

Bezpośrednie nachylenie

Przypomnijmy, że wykres funkcji liniowej \(y=kx+b\) jest linią prostą. Wywoływana jest liczba \(k=tg \alpha \). nachylenie linii prostej, a kąt \(\alfa \) jest kątem pomiędzy tą linią a osią Wółu

Jeśli \(k>0\), to \(0 Jeśli \(kRównanie stycznej do wykresu funkcji

Jeżeli punkt M(a; f(a)) należy do wykresu funkcji y = f(x) i jeżeli w tym miejscu można poprowadzić styczną do wykresu funkcji, która nie jest prostopadła do osi x, wówczas z geometrycznego znaczenia pochodnej wynika, że ​​współczynnik kątowy stycznej jest równy f "(a). Następnie opracujemy algorytm układania równania stycznej do wykresu dowolnej funkcji.

Niech na wykresie tej funkcji będzie podana funkcja y = f(x) i punkt M(a; f(a)); niech wiadomo, że f”(a) istnieje. Utwórzmy równanie na styczną do wykresu danej funkcji w danym punkcie. Równanie to, podobnie jak równanie dowolnej prostej nierównoległej do osi rzędnych, ma postać y = kx + b, więc zadaniem jest znalezienie wartości współczynników k i b.

Ze współczynnikiem kątowym k wszystko jest jasne: wiadomo, że k = f"(a). Do obliczenia wartości b wykorzystujemy fakt, że pożądana prosta przechodzi przez punkt M(a; f(a)) Oznacza to, że jeśli podstawiamy współrzędne punktu M do równania prostej, otrzymamy poprawną równość: \(f(a)=ka+b\), czyli \(b = f(a) - ka\).

Pozostaje podstawić znalezione wartości współczynników k i b do równania linii prostej:

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a )(x-a) $$

Otrzymaliśmy równanie stycznej do wykresu funkcji\(y = f(x) \) w punkcie \(x=a \).

Algorytm znajdowania równania stycznej do wykresu funkcji \(y=f(x)\)
1. Oznacz odciętą punktu stycznego literą \(a\)
2. Oblicz \(f(a)\)
3. Znajdź \(f"(x)\) i oblicz \(f"(a)\)
4. Podstaw znalezione liczby \(a, f(a), f"(a) \) do wzoru \(y=f(a)+ f"(a)(x-a) \)

Książki (podręczniki) Streszczenia Jednolitego Egzaminu Państwowego i Jednolitego Państwowego Egzaminu Testy online Gry, łamigłówki Rysowanie wykresów funkcji Słownik pisowni języka rosyjskiego Słownik slangu młodzieżowego Katalog szkół rosyjskich Katalog średnich instytucji edukacyjnych Rosji Katalog rosyjskich uniwersytetów Lista problemów Znajdowanie GCD i LCM Upraszczanie wielomianu (mnożenie wielomianów)

Rodzaj pracy: 7

Stan

Prosta y=3x+2 jest styczna do wykresu funkcji y=-12x^2+bx-10. Znajdź b, biorąc pod uwagę, że odcięta punktu stycznego jest mniejsza od zera.

Pokaż rozwiązanie

Rozwiązanie

Niech x_0 będzie odciętą punktu na wykresie funkcji y=-12x^2+bx-10, przez który przechodzi styczna do tego wykresu.

Wartość pochodnej w punkcie x_0 jest równa nachyleniu stycznej, czyli y"(x_0)=-24x_0+b=3. Natomiast punkt styczności należy jednocześnie do obu wykresu funkcja i tangens, czyli -12x_0^2+bx_0-10= 3x_0+2. Otrzymujemy układ równań \begin(przypadki) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end(przypadki)

Rozwiązując ten układ, otrzymujemy x_0^2=1, co oznacza albo x_0=-1, albo x_0=1. Zgodnie z warunkiem odciętych punkty styczne są mniejsze od zera, zatem x_0=-1, wówczas b=3+24x_0=-21.

Odpowiedź

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Prosta y=-3x+4 jest równoległa do stycznej do wykresu funkcji y=-x^2+5x-7. Znajdź odciętą punktu stycznego.

Pokaż rozwiązanie

Rozwiązanie

Współczynnik kątowy prostej do wykresu funkcji y=-x^2+5x-7 w dowolnym punkcie x_0 jest równy y"(x_0). Ale y"=-2x+5, co oznacza y" (x_0)=-2x_0+5. Kątowy współczynnik linii y=-3x+4 określony w warunku jest równy -3. Linie równoległe mają takie same współczynniki kątowe. Dlatego znajdujemy wartość x_0 taką, że = -2x_0 +5=-3.

Otrzymujemy: x_0 = 4.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Pokaż rozwiązanie

Rozwiązanie

Z rysunku określamy, że styczna przechodzi przez punkty A(-6; 2) i B(-1; 1). Oznaczmy przez C(-6; 1) punkt przecięcia prostych x=-6 i y=1, a przez \alpha kąt ABC (na rysunku widać, że jest on ostry). Następnie prosta AB tworzy kąt \pi -\alpha z dodatnim kierunkiem osi Ox, która jest rozwarta.

Jak wiadomo, tg(\pi -\alpha) będzie wartością pochodnej funkcji f(x) w punkcie x_0. Zauważ, że tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15. Stąd, korzystając ze wzorów redukcyjnych, otrzymujemy: tg(\pi -\alpha) =-tg \alpha =-\frac15=-0.2.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Prosta y=-2x-4 jest styczna do wykresu funkcji y=16x^2+bx+12. Znajdź b, biorąc pod uwagę, że odcięta punktu stycznego jest większa od zera.

Pokaż rozwiązanie

Rozwiązanie

Niech x_0 będzie odciętą punktu na wykresie funkcji y=16x^2+bx+12, przez który

jest styczna do tego wykresu.

Wartość pochodnej w punkcie x_0 jest równa nachyleniu stycznej, czyli y"(x_0)=32x_0+b=-2. Natomiast punkt styczności należy jednocześnie do obu wykresu funkcję i tangens, czyli 16x_0^2+bx_0+12=- 2x_0-4. Otrzymujemy układ równań \begin(przypadki) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end(przypadki)

Rozwiązując układ, otrzymujemy x_0^2=1, co oznacza albo x_0=-1, albo x_0=1. Zgodnie z warunkiem odciętej punkty styczne są większe od zera, zatem x_0=1, wówczas b=-2-32x_0=-34.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Rysunek przedstawia wykres funkcji y=f(x), określonej na przedziale (-2; 8). Wyznacz liczbę punktów, w których styczna do wykresu funkcji jest równoległa do prostej y=6.

Pokaż rozwiązanie

Rozwiązanie

Linia prosta y=6 jest równoległa do osi Ox. Znajdujemy zatem punkty, w których styczna do wykresu funkcji jest równoległa do osi Wółu. Na tym wykresie takie punkty są punktami ekstremalnymi (punktami maksymalnymi lub minimalnymi). Jak widać, istnieją 4 ekstrema.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Prosta y=4x-6 jest równoległa do stycznej do wykresu funkcji y=x^2-4x+9. Znajdź odciętą punktu stycznego.

Pokaż rozwiązanie

Rozwiązanie

Nachylenie stycznej do wykresu funkcji y=x^2-4x+9 w dowolnym punkcie x_0 jest równe y"(x_0). Ale y"=2x-4, co oznacza y"(x_0)= 2x_0-4. Nachylenie stycznej y =4x-7 określonej w warunku jest równe 4. Proste równoległe mają te same współczynniki kątowe. Dlatego znajdujemy wartość x_0 taką, że 2x_0-4=4.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu państwowego Unified State Exam 2017. Poziom profilu.” wyd. F. F. Łysenko, S. Yu.

Rodzaj pracy: 7
Temat: Znaczenie geometryczne pochodnych. Styczna do wykresu funkcji

Stan

Rysunek przedstawia wykres funkcji y=f(x) i styczną do niej w punkcie z odciętą x_0. Znajdź wartość pochodnej funkcji f(x) w punkcie x_0.

Pokaż rozwiązanie

Rozwiązanie

Z rysunku wynika, że ​​styczna przechodzi przez punkty A(1; 1) i B(5; 4). Oznaczmy przez C(5; 1) punkt przecięcia prostych x=5 i y=1, a przez \alpha kąt BAC (na rysunku widać, że jest on ostry). Następnie prosta AB tworzy kąt \alfa z dodatnim kierunkiem osi Ox.

Na obecnym etapie rozwoju edukacji jednym z jej głównych zadań jest kształtowanie osobowości twórczo myślącej. Zdolność twórczą uczniów można rozwijać tylko wtedy, gdy będą oni systematycznie angażowani w podstawy działalności badawczej. Podstawą wykorzystania przez uczniów swoich sił twórczych, zdolności i talentów jest kształtowana pełnoprawna wiedza i umiejętności. W związku z tym problem kształtowania systemu podstawowej wiedzy i umiejętności dla każdego tematu szkolnego kursu matematyki nie jest mały. Jednocześnie pełnoprawne umiejętności powinny być celem dydaktycznym nie poszczególnych zadań, ale ich starannie przemyślanego systemu. W najszerszym znaczeniu system jest rozumiany jako zbiór wzajemnie powiązanych, oddziałujących na siebie elementów, które charakteryzują się integralnością i stabilną strukturą.

Rozważmy technikę nauczania uczniów, jak napisać równanie stycznej do wykresu funkcji. Zasadniczo wszystkie problemy ze znalezieniem równania stycznego sprowadzają się do konieczności wybrania ze zbioru (wiązki, rodziny) prostych tych, które spełniają określony warunek - są styczne do wykresu określonej funkcji. W takim przypadku zbiór linii, z których dokonywana jest selekcja, można określić na dwa sposoby:

a) punkt leżący na płaszczyźnie xOy (środkowy ołówek linii);
b) współczynnik kątowy (równoległa wiązka linii prostych).

W związku z tym, studiując temat „Styczna do wykresu funkcji” w celu wyodrębnienia elementów układu, zidentyfikowaliśmy dwa rodzaje problemów:

1) problemy dotyczące stycznej danej przez punkt, przez który ona przechodzi;
2) problemy dotyczące stycznej wynikającej z jej nachylenia.

Szkolenie z rozwiązywania problemów stycznych przeprowadzono przy użyciu algorytmu zaproponowanego przez A.G. Mordkowicz. Zasadnicza różnica w stosunku do znanych już polega na tym, że odcięta punktu stycznego jest oznaczona literą a (zamiast x0), w związku z czym równanie stycznej przyjmuje postać

y = f(a) + f "(a)(x – a)

(porównaj z y = f(x 0) + f "(x 0)(x – x 0)). Naszym zdaniem ta technika metodologiczna pozwala uczniom szybko i łatwo zrozumieć, gdzie zapisane są współrzędne bieżącego punktu ogólne równanie styczne i gdzie znajdują się punkty styczności.

Algorytm skomponowania równania stycznego z wykresem funkcji y = f(x)

1. Oznacz odciętą punktu stycznego literą a.
2. Znajdź f(a).
3. Znajdź f „(x) i f” (a).
4. Podstaw znalezione liczby a, f(a), f „(a) do ogólnego równania stycznego y = f(a) = f „(a)(x – a).

Algorytm ten można zestawić na podstawie samodzielnej identyfikacji przez studentów operacji i kolejności ich wykonywania.

Praktyka pokazała, że ​​sekwencyjne rozwiązywanie każdego z kluczowych problemów za pomocą algorytmu pozwala rozwinąć umiejętności zapisywania równania stycznej na wykresie funkcji etapami, a kroki algorytmu służą jako punkty odniesienia dla działań . Podejście to odpowiada teorii stopniowego kształtowania się działań umysłowych opracowanej przez P.Ya. Galperin i N.F. Talyzina.

W pierwszym typie zadań zidentyfikowano dwa zadania kluczowe:

• styczna przechodzi przez punkt leżący na krzywej (zadanie 1);
• styczna przechodzi przez punkt nie leżący na krzywej (zadanie 2).

Zadanie 1. Napisz równanie stycznej do wykresu funkcji w punkcie M(3; – 2).

Rozwiązanie. Punkt M(3; – 2) jest punktem stycznym, ponieważ

1. a = 3 – odcięta punktu stycznego.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – równanie styczne.

Zadanie 2. Zapisz równania wszystkich stycznych do wykresu funkcji y = – x 2 – 4x + 2 przechodzącej przez punkt M(– 3; 6).

Rozwiązanie. Punkt M(– 3; 6) nie jest punktem styczności, gdyż f(– 3) 6 (rys. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – równanie styczne.

Styczna przechodzi przez punkt M(– 3; 6), zatem jej współrzędne spełniają równanie styczne.

6 = – za 2 – 4a + 2 – 2(a + 2)(– 3 – a),
za 2 + 6a + 8 = 0 ^ za 1 = – 4, za 2 = – 2.

Jeśli a = – 4, to równanie styczne ma postać y = 4x + 18.

Jeżeli a = – 2, to równanie styczne ma postać y = 6.

W drugim typie kluczowymi zadaniami będą:

• styczna jest równoległa do jakiejś prostej (zadanie 3);
• styczna przechodzi pod pewnym kątem do danej prostej (zadanie 4).

Zadanie 3. Zapisz równania wszystkich stycznych do wykresu funkcji y = x 3 – 3x 2 + 3, równolegle do prostej y = 9x + 1.

1. a – odcięta punktu stycznego.
2. f(a) = za 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Ale z drugiej strony f "(a) = 9 (warunek równoległości). Oznacza to, że musimy rozwiązać równanie 3a 2 – 6a = 9. Jego pierwiastki to a = – 1, a = 3 (ryc. 3 ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f „(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – równanie styczne;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – równanie styczne.

Zadanie 4. Zapisz równanie stycznej do wykresu funkcji y = 0,5x 2 – 3x + 1, przechodzącej pod kątem 45° do prostej y = 0 (rys. 4).

Rozwiązanie. Z warunku f "(a) = tan 45° znajdujemy a: a – 3 = 1 ^ a = 4.

1. a = 4 – odcięta punktu stycznego.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – równanie styczne.

Łatwo pokazać, że rozwiązanie dowolnego innego problemu sprowadza się do rozwiązania jednego lub większej liczby problemów kluczowych. Rozważmy jako przykład dwa poniższe problemy.

1. Zapisz równania stycznych do paraboli y = 2x 2 – 5x – 2, jeśli styczne przecinają się pod kątem prostym i jedna z nich dotyka paraboli w punkcie o odciętej 3 (rys. 5).

Rozwiązanie. Ponieważ podana jest odcięta punktu styczności, pierwsza część rozwiązania sprowadza się do kluczowego problemu 1.

1. a = 3 – odcięta punktu styczności jednego z boków kąta prostego.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – równanie pierwszej stycznej.

Niech a będzie kątem nachylenia pierwszej stycznej. Ponieważ styczne są prostopadłe, to jest kąt nachylenia drugiej stycznej. Z równania y = 7x – 20 pierwszej stycznej mamy tg a = 7. Znajdźmy

Oznacza to, że nachylenie drugiej stycznej jest równe .

Dalsze rozwiązanie sprowadza się do kluczowego zadania 3.

Niech B(c; f(c)) będzie zatem punktem styczności drugiej prostej

1. – odcięta drugiego punktu styczności.
2.
3.
4.
– równanie drugiej stycznej.

Notatka. Współczynnik kątowy stycznej można łatwiej znaleźć, jeśli uczniowie znają stosunek współczynników prostych prostopadłych k 1 k 2 = – 1.

2. Zapisz równania wszystkich wspólnych stycznych do wykresów funkcji

Rozwiązanie. Zadanie sprowadza się do znalezienia odciętej punktów stycznych wspólnych stycznych, czyli rozwiązania kluczowego problemu 1 w postaci ogólnej, ułożenia układu równań i następnie jego rozwiązania (rys. 6).

1. Niech a będzie odciętą punktu stycznego leżącego na wykresie funkcji y = x 2 + x + 1.
2. f(a) = za 2 + za + 1.
3. f "(a) = 2a + 1.
4. y = za 2 + za + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – za 2 .

1. Niech c będzie odciętą punktu stycznego leżącego na wykresie funkcji
2.
3. f "(c) = do.
4.

Zatem styczne są ogólne

Zatem y = x + 1 i y = – 3x – 3 są wspólnymi stycznymi.

Głównym celem rozważanych zadań jest przygotowanie studentów do samodzielnego rozpoznawania rodzaju problemu kluczowego przy rozwiązywaniu bardziej złożonych problemów wymagających określonych umiejętności badawczych (umiejętność analizowania, porównywania, uogólniania, stawiania hipotez itp.). Do takich zadań zalicza się każde zadanie, którego elementem jest zadanie kluczowe. Rozważmy jako przykład problem (odwrotny do Zadania 1) znalezienia funkcji z rodziny jej stycznych.

3. Dla jakich b i c proste y = x i y = – 2x są styczne do wykresu funkcji y = x 2 + bx + c?

Niech t będzie odciętą punktu styczności prostej y = x z parabolą y = x 2 + bx + c; p jest odciętą punktu styczności prostej y = – 2x z parabolą y = x 2 + bx + c. Wtedy równanie styczne y = x przyjmie postać y = (2t + b)x + c – t 2 , a równanie styczne y = – 2x przyjmie postać y = (2p + b)x + c – p 2 .

Ułóżmy i rozwiążmy układ równań

Odpowiedź: