Seria funkcjonalna. Seria potęgowa.
Zakres zbieżności szeregu

Śmiech bez powodu jest oznaką d'Alemberta

Wybiła godzina szeregów funkcjonalnych. Aby skutecznie opanować temat, a w szczególności tę lekcję, musisz dobrze rozumieć zwykłe szeregi liczbowe. Powinieneś dobrze rozumieć, czym jest szereg i potrafić zastosować kryteria porównawcze w celu sprawdzenia szeregu pod kątem zbieżności. Tak więc, jeśli dopiero zacząłeś studiować ten temat lub jesteś początkujący w wyższej matematyce, niezbędny przepracuj kolejno trzy lekcje: Rzędy dla manekinów,Objaw D'Alemberta. Objawy Cauchy’ego I Naprzemienne rzędy. Próba Leibniza. Zdecydowanie wszystkie trzy! Jeśli masz podstawową wiedzę i umiejętności rozwiązywania problemów z szeregami liczbowymi, radzenie sobie z szeregami funkcjonalnymi będzie dość proste, ponieważ nie ma zbyt wiele nowego materiału.

Na tej lekcji przyjrzymy się pojęciu szeregu funkcyjnego (czym w ogóle jest), zapoznamy się z szeregami potęgowymi, które można znaleźć w 90% praktycznych zadań i nauczymy się, jak rozwiązać typowy typowy problem znalezienia promienia zbieżności, przedziału zbieżności i obszaru zbieżności szeregu potęgowego. Następnie polecam rozważyć materiał na temat rozwinięcie funkcji w szeregi potęgowe, a początkującemu zostanie udzielona pierwsza pomoc. Po chwili złapania oddechu przechodzimy do następnego poziomu:

Również w dziale serii funkcjonalnych jest ich wiele zastosowania obliczeń przybliżonych, i w pewnym sensie wyróżniają się serie Fouriera, którym z reguły poświęca się osobny rozdział w literaturze edukacyjnej. Mam tylko jeden artykuł, ale jest długi i zawiera wiele, wiele dodatkowych przykładów!

Punkty orientacyjne są ustawione, chodźmy:

Pojęcie szeregu funkcyjnego i szeregu potęgowego

Jeśli granica okaże się nieskończona, wówczas algorytm rozwiązania również kończy swoją pracę i podajemy ostateczną odpowiedź na zadanie: „Szereg zbiega się w ” (lub w którymkolwiek „). Patrz przypadek nr 3 poprzedniego akapitu.

Jeśli granica okaże się ani zerem, ani nieskończonością, to mamy w praktyce najczęstszy przypadek nr 1 – szereg zbiega się w pewnym przedziale.

W tym przypadku granica wynosi . Jak znaleźć przedział zbieżności szeregu? Uzupełniamy nierówność:

W KAŻDE zadanie tego typu po lewej stronie nierówności powinno być wynik obliczenia limitu, a po prawej stronie nierówności – rygorystycznie jednostka. Nie będę dokładnie wyjaśniał, dlaczego jest taka nierówność i dlaczego jest jedna po prawej stronie. Lekcje są nastawione na praktykę i już bardzo dobrze, że moje opowiadania nie zawiodły kadry nauczycielskiej i niektóre twierdzenia stały się jaśniejsze.

Technika pracy z modułem i rozwiązywania podwójnych nierówności została szczegółowo omówiona w pierwszym roku artykułu Dziedzina funkcji, ale dla wygody postaram się opisać wszystkie działania tak szczegółowo, jak to możliwe. Ujawniamy nierówność z modułem zgodnie z regułą szkolną . W tym przypadku:

Połowa drogi już za nami.

W drugim etapie należy zbadać zbieżność szeregu na końcach znalezionego przedziału.

Najpierw bierzemy lewy koniec przedziału i podstawiamy go do naszego szeregu potęgowego:

Na

Otrzymaliśmy szereg liczbowy i musimy sprawdzić go pod kątem zbieżności (zadanie znane już z poprzednich lekcji).

1) Szereg jest naprzemienny.
2) – wyrazy szeregu zmniejszają moduł. Co więcej, każdy kolejny element szeregu jest mniejszy od poprzedniego w wartości bezwzględnej: , co oznacza, że ​​spadek jest monotonny.
Wniosek: szereg jest zbieżny.

Korzystając z serii złożonej z modułów dowiemy się dokładnie jak:
– jest zbieżny („szereg „standardowy” z rodziny uogólnionych szeregów harmonicznych).

Zatem wynikowy szereg liczbowy jest zbieżny absolutnie.

Na – zbiega się.

! Przypominam ci że każdy zbieżny szereg dodatni jest również absolutnie zbieżny.

Zatem szereg potęgowy jest zbieżny i to absolutnie na obu końcach znalezionego przedziału.

Odpowiedź: obszar zbieżności badanego szeregu potęgowego:

Inna forma odpowiedzi ma prawo do życia: szereg jest zbieżny, jeśli

Czasami sformułowanie problemu wymaga wskazania promienia zbieżności. Jest oczywiste, że w rozważanym przykładzie.

Przykład 2

Znajdź obszar zbieżności szeregu potęgowego

Rozwiązanie: znajdujemy przedział zbieżności szeregu używając objaw d'Alemberta (ale nie atrybut BY! – taki atrybut nie istnieje dla szeregów funkcjonalnych):

Szereg zbiega się w godz

Lewy musimy wyjechać tylko, więc mnożymy obie strony nierówności przez 3:

– Seria jest naprzemienna.
– – wyrazy szeregu zmniejszają moduł. Każdy kolejny element szeregu jest mniejszy od poprzedniego w wartości bezwzględnej: , co oznacza, że ​​spadek jest monotonny.

Wniosek: szereg jest zbieżny.

Zbadajmy to pod kątem natury zbieżności:

Porównajmy ten szereg z szeregiem rozbieżnym.
Stosujemy ograniczające kryterium porównania:

Otrzymuje się liczbę skończoną różną od zera, co oznacza, że ​​szereg odbiega od szeregu.

Zatem szereg jest zbieżny warunkowo.

2) Kiedy – jest rozbieżny (zgodnie z tym, co zostało udowodnione).

Odpowiedź: Obszar zbieżności badanego szeregu potęgowego: . Gdy szereg jest zbieżny warunkowo.

W rozpatrywanym przykładzie obszarem zbieżności szeregu potęgowego jest połowa przedziału, a we wszystkich punktach przedziału szereg potęgowy zbiega się absolutnie i w tym momencie, jak się okazało – warunkowo.

Przykład 3

Znajdź przedział zbieżności szeregu potęgowego i zbadaj jego zbieżność na końcach znalezionego przedziału

To jest przykład, który możesz rozwiązać samodzielnie.

Przyjrzyjmy się kilku przykładom, które są rzadkie, ale występują.

Przykład 4

Znajdź obszar zbieżności szeregu:

Rozwiązanie: Korzystając z testu d'Alemberta znajdujemy przedział zbieżności tego szeregu:

(1) Tworzymy stosunek kolejnego członka szeregu do poprzedniego.

(2) Pozbywamy się czteropiętrowej frakcji.

(3) Zgodnie z zasadą działania na potęgach, kostki zaliczamy do jednej potęgi. W liczniku sprytnie rozszerzamy stopień, czyli tzw. Układamy to tak, aby w kolejnym kroku móc skrócić ułamek o . Opisujemy szczegółowo silnię.

(4) Pod sześcianem dzielimy licznik przez mianownik wyraz po wyrazie, wskazując, że . W ułamku redukujemy wszystko, co da się zredukować. Wyciągamy współczynnik poza znak graniczny; można go usunąć, ponieważ nie ma w nim nic, co zależy od zmiennej „dynamicznej” „en”. Należy pamiętać, że znak modułu nie jest rysowany - z tego powodu, że przyjmuje wartości nieujemne dla dowolnego „x”.

W granicy otrzymuje się zero, co oznacza, że ​​możemy podać ostateczną odpowiedź:

Odpowiedź: Szereg zbiega się w godz

Ale początkowo wydawało się, że ten rząd z „strasznym nadzieniem” będzie trudny do rozwiązania. Zero lub nieskończoność w limicie to niemal prezent, bo rozwiązanie jest zauważalnie zmniejszone!

Przykład 5

Znajdź obszar zbieżności szeregu

To jest przykład, który możesz rozwiązać samodzielnie. Bądź ostrożny ;-) Pełne rozwiązanie znajduje się na końcu lekcji.

Przyjrzyjmy się jeszcze kilku przykładom, które zawierają element nowości w zakresie zastosowania technik technicznych.

Przykład 6

Znajdź przedział zbieżności szeregu i zbadaj jego zbieżność na końcach znalezionego przedziału

Rozwiązanie: Wspólny termin szeregu potęgowego zawiera współczynnik zapewniający zmienność znaku. Algorytm rozwiązania jest całkowicie zachowany, ale przy ustalaniu limitu ignorujemy (nie zapisujemy) ten czynnik, ponieważ moduł niszczy wszystkie „minusy”.

Przedział zbieżności szeregu wyznaczamy za pomocą testu d'Alemberta:

Stwórzmy standardową nierówność:
Szereg zbiega się w godz
Lewy musimy wyjechać tylko moduł, więc mnożymy obie strony nierówności przez 5:

Teraz otwieramy moduł w znany nam sposób:

W środku podwójnej nierówności należy pozostawić tylko „X”; w tym celu odejmujemy 2 od każdej części nierówności:

– przedział zbieżności badanego szeregu potęgowego.

Badamy zbieżność szeregu na końcach znalezionego przedziału:

1) Podstaw wartość do naszego szeregu potęgowego :

Bądź bardzo ostrożny, mnożnik nie zapewnia zmiany znaku dla żadnego naturalnego „en”. Wynikowy minus wyciągamy poza szereg i zapominamy o tym, ponieważ on (jak każda stała czynnikowa) w żaden sposób nie wpływa na zbieżność lub rozbieżność szeregu liczbowego.

Proszę zwrócić uwagę jeszcze razże w trakcie podstawienia wartości do wyrazu ogólnego szeregu potęgowego nasz współczynnik uległ zmniejszeniu. Gdyby tak się nie stało, oznaczałoby to, że albo źle obliczyliśmy limit, albo źle rozbudowaliśmy moduł.

Musimy zatem sprawdzić szereg liczbowy pod kątem zbieżności. Tutaj najłatwiej jest zastosować ograniczające kryterium porównania i porównać ten szereg z rozbieżnym szeregiem harmonicznym. Ale szczerze mówiąc, jestem strasznie zmęczony ograniczającym znakiem porównania, więc dodam trochę urozmaicenia do rozwiązania.

Zatem szereg jest zbieżny w punkcie

Mnożymy obie strony nierówności przez 9:

Wyciągamy korzeń z obu części, pamiętając stary szkolny dowcip:


Rozbudowa modułu:

i dodaj jeden do wszystkich części:

– przedział zbieżności badanego szeregu potęgowego.

Zbadajmy zbieżność szeregu potęgowego na końcach znalezionego przedziału:

1) Jeżeli , to otrzymuje się następujący szereg liczbowy:

Mnożnik zniknął bez śladu, gdyż dla dowolnej wartości naturalnej „en” .

Seria potęgowa nazywa się szeregiem funkcjonalnym formy

Tutaj X – zmienna rzeczywista. Takty muzyczne A N (N = 0, 1, 2, … ) są nazywane współczynniki szeregu. W dalszej części ograniczymy się do przypadku, gdy wszystko A N i wielkość X 0 – liczby rzeczywiste. Nazywa się także szeregiem potęgowym (9,5). blisko stopni różnicyX  X 0 .

Jeśli X 0 = 0 , wówczas otrzymujemy szereg potęgowy postaci

, (9.6)

co się nazywa następny stopieńX .

Szereg potęgowy (9.5) sprowadza się do postaci (9.6) za pomocą prostej transformacji X  X 0 = T (przenieś początek na oś liczbową). Z tego powodu teoria władzy

serie (9.5) i (9.6) są powszechne. Dlatego w przyszłości ograniczymy się do rozważenia głównych właściwości szeregu postaci (9.6).

Rozważając szeregi potęgowe, główną kwestią jest ich wyznaczenie obszary konwergencji, tj. zbiory tych wartości X , w którym szereg jest zbieżny.

Problem ten rozwiązuje się na podstawie Twierdzenia Abela .

Jeśli szereg potęgowy (9.6) zbiega się przy pewnej wartościX = X 1  0 , to jest zbieżny absolutnie dla wszystkich wartościX , spełniając nierówność  X  <  X 1  .

Jeśli szereg jest rozbieżny przy określonej wartości X = X 2 , to się rozchodzi i dla wszystkichX ,spełniając nierówność  X  >  X 2 .

Twierdzenie Abela pozwala ocenić położenie punktów zbieżności i rozbieżności szeregu potęgowego (9.6).

Rzeczywiście, jeśli X 1 jest punktem zbieżności, to cały przedział (   X 1  ,  X 1 ) jest wypełniona punktami zbieżności absolutnej.

Jeśli X 2 jest punktem rozbieżności, to przedziały (   ,   X 2 ) i ( X 2  , +  )składają się z punktów rozbieżności.

Z tego możemy wywnioskować, że istnieje taka liczba R , co w X  < R szereg potęgowy jest absolutnie zbieżny, a dla  X  > R – różni się.

Interwał (  R , R ) nazywa się przedział zbieżności szeregi potęgowe (9.6). Numer R zwany promień zbieżności szereg potęgowy.

Należy zauważyć, że przedział zbieżności niektórych szeregów reprezentuje całą oś liczbową (w tym przypadku R =  ), dla innych degeneruje się do jednego punktu (przypadek R = 0 ). Na X =  R , tj. na końcach przedziału zbieżności szereg może być zbieżny bezwzględnie, warunkowo lub rozbieżny. Aby wyjaśnić zachowanie szeregu w punktach końcowych, konieczne jest podstawienie szeregu w wyrażeniu X wartości  R i sprawdź powstałe dwa szeregi liczbowe pod kątem zbieżności. Ten problem został rozwiązany indywidualnie dla każdego konkretnego wiersza.

Po zastosowaniu do szeregów potęgowych postaci (9.5) otrzymane wyniki ulegają modyfikacji jedynie w ten sposób, że środek zbieżności znajduje się w punkcie X = X 0 , nie w tym momencie X = 0 , tj. przedział zbieżności szeregu potęgowego (9,5) jest symetryczny względem punktu X = X 0 i reprezentuje przedział X 0  R < X < X 0 + R .

Zauważ, że aby znaleźć przedział zbieżności szeregu potęgowego (9.6), możemy zbadać szereg

, (9.7)

składa się z modułów członków danego szeregu, gdyż przedziały zbieżności tych szeregów pokrywają się.

Do wyznaczenia zbieżności szeregów (9.7), których wyrazy są dodatnie, stosuje się zwykle testy zbieżności D’Alemberta lub Cauchy’ego.

Załóżmy, że istnieje granica
.

Następnie, według kryterium d'Alemberta, szereg (9.7) jest zbieżny dla
, tj. jeśli
, i różni się w
, tj. jeśli
. Zatem szereg ten zbiega się w przedziale
i rozbiega się poza nim, tj. promień zbieżności jest równy
.

Notatki.

1) Jeśli A = 0 , to szereg pierwotny jest zbieżny bezwzględnie dla wszystkich wartości liczbowych X , ponieważ w tym przypadku mamy  X   A = 0 < 1 dla kogokolwiek X . W tym przypadku promień zbieżności R =  .

2) Jeśli A =  , To oryginalny szereg zbiega się w jednym punkcie X = 0 . Wcześniej przyjęto, że w tym przypadku R = 0 .

3) Podobnie, aby wyznaczyć przedział zbieżności, można skorzystać z testu Cauchy’ego, jeśli taki istnieje
. W tym przypadku
.

4) Przedział zbieżności można wyznaczyć bezpośrednio za pomocą testu D’Alemberta lub Cauchy’ego.

Przykład 9.11. Wyznacz obszar zbieżności szeregu
.

Rozwiązanie. Tutaj
. Dlatego,

.

A więc przerwa
jest przedziałem zbieżności danego szeregu.

Przeanalizujmy zachowanie szeregu na końcach przedziału zbieżności. Na
serial przybierze formę
. Jest to szereg harmoniczny, jest rozbieżny. Na
serial przybierze formę
. Ten szereg przemienny jest zbieżny warunkowo, gdyż łatwo sprawdzić, czy spełnione są warunki kryterium Leibniza, a szereg modułów różni się.

Więc kiedy
Szereg jest zbieżny bezwzględnie, gdy
Szereg jest zbieżny warunkowo, we wszystkich pozostałych punktach szereg jest rozbieżny.

Przykład 9.12. Znajdź obszar zbieżności szeregu
.

Rozwiązanie. Skorzystajmy z testu Cauchy’ego. Mamy

Zatem szereg jest zbieżny bezwzględnie tylko wtedy, gdy X =  1 , a we wszystkich pozostałych punktach osi liczbowej szereg jest rozbieżny. Promień zbieżności R = 0 .

Przykład 1. Znajdź obszar zbieżności szeregu potęgowego:

A) ; B) ;

V) ; G)
;

D)
.

A) Znajdźmy promień zbieżności R. Ponieważ
,
, To

.

X
, czyli przedział zbieżności szeregu
.

Na
otrzymujemy szereg liczbowy . Szereg ten jest zbieżny, ponieważ jest uogólnionym szeregiem harmonicznym Na
.

Na
otrzymujemy szereg liczbowy
. Szereg ten jest absolutnie zbieżny, ponieważ szereg składa się z wartości bezwzględnych jego wyrazów , zbieżny.

.

B) Znajdźmy promień zbieżności R. Ponieważ
, To
.

Zatem przedział zbieżności szeregu
.

Zbieżność tego szeregu badamy na końcach przedziału zbieżności.

Na
mamy szereg liczbowy

.

Na
mamy szereg liczbowy
. Szereg ten jest rozbieżny, ponieważ
nie istnieje.

Zatem obszar zbieżności tego szeregu
.

V) Znajdźmy promień zbieżności R. Ponieważ
,
To
.

Zatem przedział zbieżności
. Obszar zbieżności tego szeregu pokrywa się z przedziałem zbieżności, czyli szereg jest zbieżny dla dowolnej wartości zmiennej X.

G) Znajdźmy promień zbieżności R. Ponieważ
,
To
.

Ponieważ
, to szereg jest zbieżny tylko w punkcie
. Oznacza to, że obszar zbieżności tego szeregu wynosi jeden punkt
.

D) Znajdźmy promień zbieżności R.

Ponieważ
,
, To

.

Tak więc seria jest zbieżna dla absolutnie wszystkich X, spełniając nierówność
, to jest
.

Stąd
− przedział zbieżności,
− promień zbieżności.

Zbadajmy ten szereg pod kątem zbieżności na końcach przedziału zbieżności.

Na
otrzymujemy szereg liczbowy

,

który jest rozbieżny (szereg harmoniczny).

Na
otrzymujemy szereg liczbowy
, który jest zbieżny warunkowo (szereg jest zbieżny według kryterium Leibniza, a szereg złożony z wartości bezwzględnych jego członków jest rozbieżny, gdyż jest harmoniczny).

Zatem obszar zbieżności szeregu
.

2.3. Szereg Taylora i Maclaurina.

Rozwinięcie funkcji w szeregi potęgowe.

Zastosowanie szeregów potęgowych do obliczeń przybliżonych

Przykłady rozwiązywania problemów

Przykład 1. Rozwiń funkcję w szereg potęgowy:

A)
; B)
;

V)
; G)
.

A) Zastąpienie we wzorze
X NA
, otrzymujemy pożądane rozwinięcie:

Gdzie

B) Podstawianie w równości

Gdzie
X NA
, otrzymujemy pożądane rozwinięcie:

V) Funkcję tę można zapisać w następujący sposób:
. Aby znaleźć żądaną serię, wystarczy rozwinąć

Gdzie
zastąpić
. Następnie otrzymujemy:

G) Funkcję tę można przepisać w następujący sposób: .

Funkcjonować
można rozszerzyć do szeregu potęgowego, wstawiając szereg dwumianowy
, otrzymamy.

Gdzie
.

Aby uzyskać pożądane rozwinięcie wystarczy pomnożyć otrzymany szereg (ze względu na bezwzględną zbieżność tych szeregów).

Stąd,

, Gdzie
.

Przykład 2. Znajdź przybliżone wartości tych funkcji:

A)
z dokładnością 0,0001;

B)
z dokładnością do 0,00001.

A) Ponieważ
, a następnie do rozwinięcia funkcji, gdzie
zamieńmy
:

Lub

Ponieważ
, to wymagana dokładność zostanie zapewniona, jeśli ograniczymy się tylko do dwóch pierwszych wyrazów powstałego rozwinięcia.

.

Używamy szeregu dwumianowego

Gdzie
.

Wierzyć
I
, otrzymujemy następujące rozwinięcie:

Jeśli w ostatniej serii naprzemiennej zostaną uwzględnione tylko dwa pierwsze wyrazy, a pozostałe zostaną odrzucone, wówczas błąd w obliczeniach
nie przekroczy 0,000006 w wartości bezwzględnej. Następnie błąd w obliczeniach
nie przekroczy tej liczby. Stąd,

Przykład 3. Oblicz z dokładnością do 0,001:

A)
; B)
.

A)
.

Rozwińmy całkę w szereg potęgowy. Aby to zrobić, podstawimy szereg dwumianowy
i wymienić X NA :

.

Od segmentu integracji
należy do obszaru zbieżności otrzymanego szeregu
, wówczas będziemy integrować termin po terminie w określonych granicach:

.

W wynikowej serii naprzemiennych znaków czwarty wyraz ma wartość bezwzględną mniejszą niż 0,001. W rezultacie wymagana dokładność zostanie zapewniona, jeśli uwzględni się tylko trzy pierwsze wyrazy szeregu.

.

Ponieważ pierwszy z odrzuconych terminów ma znak minus, wynikowa przybliżona wartość będzie nadwyżka. Dlatego odpowiedź w granicach 0,001 to 0,487.

B) Przedstawmy najpierw całkę jako szereg potęgowy. Zastąpmy w rozwinięciu funkcji

Gdzie

X NA
, otrzymujemy:

Następnie
.

Powstały szereg przemienny spełnia warunki kryterium Leibniza. Czwarty wyraz szeregu ma wartość bezwzględną mniejszą niż 0,001. Aby zapewnić wymaganą dokładność, wystarczy znaleźć sumę trzech pierwszych wyrazów.

Stąd,
.

Wśród szeregów funkcjonalnych najważniejsze miejsce zajmują szeregi potęgowe.

Szereg potęgowy jest szeregiem

których wyrazy są funkcjami potęgowymi ułożonymi w rosnące nieujemne potęgi całkowite X, A C0 , C 1 , C 2 , C N - wartości stałe. Takty muzyczne C1 , C 2 , C N - współczynniki wyrazów szeregu, C0 - członek wolny. Wyrazy szeregu potęgowego są zdefiniowane na całej osi liczbowej.

Zapoznajmy się z koncepcją obszary zbieżności szeregów potęgowych. Jest to zbiór wartości zmiennej X, dla którego szereg jest zbieżny. Szeregi potęgowe mają dość prosty obszar zbieżności. Dla rzeczywistych wartości zmiennych X obszar zbieżności składa się albo z jednego punktu, albo jest pewnym przedziałem (przedziałem zbieżności), albo pokrywa się z całą osią Wół .

Podczas podstawienia wartości do szeregu potęgowego X= 0 spowoduje utworzenie serii liczb

C0 +0+0+...+0+... ,

który zbiega się.

Dlatego kiedy X= 0 dowolny szereg potęgowy jest zbieżny, a zatem jego obszar konwergencji nie może być zbiorem pustym. Struktura obszaru zbieżności wszystkich szeregów potęgowych jest taka sama. Można to ustalić korzystając z następującego twierdzenia.

Twierdzenie 1 (twierdzenie Abela). Jeśli szereg potęgowy zbiega się przy pewnej wartości X = X 0 , różny od zera, to jest zbieżny, a w dodatku bezwzględny dla wszystkich wartości |X| < |X 0 | . Uwaga: zarówno wartość początkowa „X wynosi zero”, jak i dowolna wartość „X” porównywana z wartością początkową są brane modulo – bez uwzględnienia znaku.

Konsekwencja. Jeśli szeregi potęgowe są rozbieżne przy jakiejś wartości X = X 1 , to jest rozbieżne dla wszystkich wartości |X| > |X 1 | .

Jak już dowiedzieliśmy się wcześniej, każdy szereg potęgowy zbiega się przy tej wartości X= 0. Istnieją szeregi potęgowe, które są zbieżne tylko wtedy, gdy X= 0 i rozbieżne dla innych wartości X. Wyłączając ten przypadek z rozważań, zakładamy, że szereg potęgowy jest zbieżny przy pewnej wartości X = X 0 , różny od zera. Wtedy zgodnie z twierdzeniem Abela zbiega się on we wszystkich punktach przedziału ]-| X0 |, |X 0 |[ (przedział, którego lewą i prawą granicę stanowią wartości x, przy których zbiega się szereg potęgowy, przyjmowany odpowiednio ze znakiem minus i plusem), symetryczny względem początku.

Jeśli szereg potęgowy rozbiega się przy pewnej wartości X = X 1 , wówczas, zgodnie z twierdzeniem Abela, jest on rozbieżny we wszystkich punktach poza odcinkiem [-| X1 |, |X 1 |] . Wynika z tego, że dla dowolnego szeregu potęgowego istnieje przedział symetryczny względem początku, tzw przedział zbieżności , w każdym punkcie którego szereg się zbiega, na granicach może się zbiegać lub rozchodzić, i niekoniecznie w tym samym czasie, a poza odcinkiem szereg jest rozbieżny. Numer R nazywa się promieniem zbieżności szeregu potęgowego.

W szczególnych przypadkach przedział zbieżności szeregów potęgowych może zdegenerować się do punktu (wtedy szereg jest zbieżny tylko wtedy, gdy X= 0 i tak się to przyjmuje R= 0) lub reprezentują całą oś liczbową (wtedy szereg zbiega się we wszystkich punktach osi liczbowej i zakłada się, że ).

Zatem wyznaczenie obszaru zbieżności szeregu potęgowego polega na wyznaczeniu jego promień zbieżności R i badanie zbieżności szeregu na granicach przedziału zbieżności (at ).

Twierdzenie 2. Jeżeli wszystkie współczynniki szeregu potęgowego, zaczynając od pewnego, są różne od zera, wówczas jego promień zbieżności jest równy granicy w stosunku wartości bezwzględnych współczynników wspólnych kolejnych członków szeregu , tj.

Przykład 1. Znajdź obszar zbieżności szeregu potęgowego

Rozwiązanie. Tutaj

Korzystając ze wzoru (28) wyznaczamy promień zbieżności tego szeregu:

Przeanalizujmy zbieżność szeregu na końcach przedziału zbieżności. Przykład 13 pokazuje, że ten szereg jest zbieżny w X= 1 i różni się w X= -1. W związku z tym obszar zbieżności jest połową przedziału.

Przykład 2. Znajdź obszar zbieżności szeregu potęgowego

Rozwiązanie. Współczynniki szeregu są dodatnie i

Znajdźmy granicę tego stosunku, tj. promień zbieżności szeregu potęgowego:

Przeanalizujmy zbieżność szeregu na końcach przedziału. Podstawianie wartości X= -1/5 i X= 1/5 w tym wierszu daje:

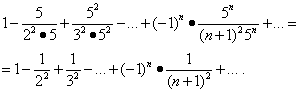
Pierwszy z tych szeregów jest zbieżny (patrz przykład 5). Ale wtedy, na mocy twierdzenia z części „Zbieżność absolutna”, drugi szereg również jest zbieżny, a obszarem jego zbieżności jest odcinek

Przykład 3. Znajdź obszar zbieżności szeregu potęgowego

Rozwiązanie. Tutaj

Korzystając ze wzoru (28) wyznaczamy promień zbieżności szeregu:

Przeanalizujmy zbieżność szeregu dla wartości . Zastępując je w tym szeregu, odpowiednio otrzymujemy

Obydwa szeregi są rozbieżne, ponieważ nie jest spełniony warunek konieczny zbieżności (ich wspólne wyrazy nie dążą do zera w punkcie ). Zatem na obu końcach przedziału zbieżności szereg ten jest rozbieżny, a obszarem jego zbieżności jest ten przedział.

Przykład 5. Znajdź obszar zbieżności szeregu potęgowego

Rozwiązanie. Znajdujemy relację gdzie , i :

Według wzoru (28) promień zbieżności tego szeregu

,

oznacza to, że szereg jest zbieżny tylko wtedy, gdy X= 0 i różni się dla innych wartości X.

Przykłady pokazują, że na końcach przedziału zbieżności szereg zachowuje się inaczej. W przykładzie 1 na jednym końcu przedziału zbieżności szereg jest zbieżny, a na drugim rozbieżny, w przykładzie 2 zbiega się na obu końcach, w przykładzie 3 jest rozbieżny na obu końcach.

Wzór na promień zbieżności szeregu potęgowego otrzymuje się przy założeniu, że wszystkie współczynniki wyrazów szeregu, począwszy od pewnego punktu, są różne od zera. Dlatego tylko w tych przypadkach dopuszczalne jest zastosowanie wzoru (28). Jeżeli warunek ten zostanie naruszony, należy szukać promienia zbieżności szeregu potęgowego objaw d'Alemberta lub poprzez zastąpienie zmiennej przekształcenie szeregu do postaci, w której spełniony jest określony warunek.

Przykład 6. Znajdź przedział zbieżności szeregu potęgowego

Rozwiązanie. Seria ta nie zawiera terminów o stopniu nieparzystym X. Dlatego przekształcamy serię, ustawiając . Wtedy otrzymamy serię

znaleźć promień zbieżności, dla którego możemy zastosować wzór (28). Ponieważ , a , to promień zbieżności tego szeregu

Z równości otrzymujemy zatem szereg ten zbiega się na przedziale .

Suma szeregów potęgowych. Różniczkowanie i całkowanie szeregów potęgowych

Niech dla szeregu potęgowego

promień zbieżności R> 0, tj. ten szereg jest zbieżny na przedziale .

Następnie każdą wartość X z przedziału zbieżności odpowiada pewnej sumie szeregu. Zatem suma szeregów potęgowych jest funkcją X na przedziale zbieżności. Oznaczanie tego przez F(X), możemy napisać równość

rozumiejąc to w tym sensie, że jest to suma szeregu w każdym punkcie X z przedziału zbieżności jest równa wartości funkcji F(X) w tym momencie. W tym samym sensie powiemy, że szereg potęgowy (29) zbiega się do funkcji F(X) w przedziale zbieżności.

Poza przedziałem zbieżności równość (30) nie ma sensu.

Przykład 7. Znajdź sumę szeregu potęgowego

Rozwiązanie. Jest to szereg geometryczny, dla którego A= 1, a Q= X. Dlatego jego suma jest funkcją . Szereg jest zbieżny, jeśli , i jest jego przedziałem zbieżności. Dlatego równość

obowiązuje tylko dla wartości, chociaż jest to funkcja zdefiniowane dla wszystkich wartości X, z wyjątkiem X= 1.

Można udowodnić, że suma szeregów potęgowych F(X) jest ciągła i różniczkowalna na dowolnym przedziale przedziału zbieżności, w szczególności w dowolnym punkcie przedziału zbieżności szeregu.

Przedstawmy twierdzenia o różniczkowaniu wyrazowym i całkowaniu szeregów potęgowych.

Twierdzenie 1. Szereg potęgowy (30) w przedziale jego zbieżności można różniczkować wyraz po wyrazie nieograniczoną liczbę razy, a powstałe szeregi potęgowe mają taki sam promień zbieżności jak szeregi pierwotne, a ich sumy są odpowiednio równe .

Twierdzenie 2. Szereg potęgowy (30) można całkować wyraz po wyrazie nieograniczoną liczbę razy w zakresie od 0 do X, if , i wynikowy szereg potęgowy mają ten sam promień zbieżności co szereg pierwotny, a ich sumy są odpowiednio równe

Rozwinięcie funkcji w szeregi potęgowe

Niech będzie podana funkcja F(X), który należy rozwinąć w szereg potęgowy, tj. przedstawić w postaci (30):

Zadanie polega na wyznaczeniu współczynników rząd (30). Aby to zrobić, różnicując równość (30) termin po terminie, konsekwentnie znajdujemy:

……………………………………………….. (31)

Zakładając równości (30) i (31) X= 0, znajdujemy

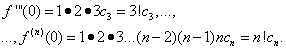
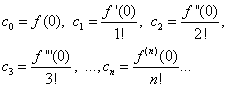
Podstawiając znalezione wyrażenia do równości (30), otrzymujemy

(32)

Znajdźmy rozwinięcie w szereg Maclaurina niektórych funkcji elementarnych.

Przykład 8. Rozwiń funkcję w szeregu Maclaurina

Rozwiązanie. Pochodne tej funkcji pokrywają się z samą funkcją:

Dlatego kiedy X= 0 mamy

Podstawiając te wartości do wzoru (32) otrzymujemy pożądane rozwinięcie:

(33)

Szereg ten zbiega się na całej osi liczbowej (jej promieniu zbieżności).