Identyczne przekształcenia wyrażeń zawierających potęgi i logarytmy. Wyrażenia logarytmiczne

Przyjrzymy się teraz konwersji wyrażeń zawierających logarytmy z ogólnej perspektywy. Tutaj zbadamy nie tylko transformację wyrażeń za pomocą właściwości logarytmów, ale także rozważymy transformację wyrażeń za pomocą logarytmów ogólnych, które zawierają nie tylko logarytmy, ale także potęgi, ułamki, pierwiastki itp. Tradycyjnie cały materiał zaopatrzymy w typowe przykłady ze szczegółowymi opisami rozwiązań.

Nawigacja strony.

Wyrażenia logarytmiczne i wyrażenia logarytmiczne

Robienie rzeczy z ułamków zwykłych

W poprzednim akapicie sprawdziliśmy podstawowe przekształcenia przeprowadzane na poszczególnych ułamkach zawierających logarytmy. Przekształcenia te można oczywiście przeprowadzić dla każdego pojedynczego ułamka będącego częścią bardziej złożonego wyrażenia, na przykład reprezentującego sumę, różnicę, iloczyn i iloraz podobnych ułamków. Ale oprócz pracy z pojedynczymi ułamkami, konwertowanie wyrażeń tego typu często wiąże się z wykonaniem odpowiednich operacji na ułamkach. Następnie przyjrzymy się zasadom, według których te działania są przeprowadzane.

Już od klas V-VI znamy zasady według których są one realizowane. W artykule ogólne spojrzenie na operacje na ułamkach zwykłych Rozszerzyliśmy te reguły z ułamków zwykłych na ułamki o ogólnej postaci A/B, gdzie A i B są wyrażeniami numerycznymi, dosłownymi lub zmiennymi, a B nie jest identycznie równe zero. Oczywiste jest, że ułamki z logarytmami są szczególnymi przypadkami ułamków ogólnych. Pod tym względem jasne jest, że operacje na ułamkach zawierających logarytmy w ich zapisach są przeprowadzane według tych samych zasad. Mianowicie:

• Aby dodać lub odjąć dwa ułamki zwykłe o tych samych mianownikach, należy odpowiednio dodać lub odjąć liczniki, ale pozostawić mianownik bez zmian.
• Aby dodać lub odjąć dwa ułamki zwykłe o różnych mianownikach, należy sprowadzić je do wspólnego mianownika i wykonać odpowiednie czynności zgodnie z poprzednią zasadą.
• Aby pomnożyć dwa ułamki, musisz zapisać ułamek, którego licznik jest iloczynem liczników pierwotnych ułamków, a mianownik jest iloczynem mianowników.
• Aby podzielić ułamek na ułamek, należy pomnożyć dzielony ułamek przez ułamek będący odwrotnością dzielnika, czyli przez ułamek z zamienionymi licznikami i mianownikami.

Oto kilka przykładów wykonywania operacji na ułamkach zawierających logarytmy.

Przykład.

Wykonaj działania na ułamkach zawierających logarytmy: a) , b) , V) , G) .

Rozwiązanie.

a) Mianowniki dodawanych ułamków są oczywiście takie same. Dlatego zgodnie z zasadą dodawania ułamków o tych samych mianownikach dodajemy liczniki, a mianownik pozostawiamy bez zmian: .

b) Tutaj mianowniki są różne. Dlatego najpierw potrzebujesz zamień ułamki zwykłe na ten sam mianownik. W naszym przypadku mianowniki są już przedstawione w postaci iloczynów, wystarczy, że weźmiemy mianownik pierwszego ułamka i dodamy do niego brakujące czynniki z mianownika drugiego ułamka. Otrzymujemy w ten sposób wspólny mianownik formy . W tym przypadku odjęte ułamki sprowadza się do wspólnego mianownika za pomocą dodatkowych czynników w postaci odpowiednio logarytmu i wyrażenia x 2 ·(x+1). Następnie pozostaje tylko odjąć ułamki o tych samych mianownikach, co nie jest trudne.

Rozwiązaniem jest zatem:

c) Wiadomo, że wynikiem mnożenia ułamków jest ułamek, którego licznik jest iloczynem liczników, a mianownik jest iloczynem mianowników, dlatego

Łatwo zobaczyć, że możesz redukując ułamek przez dwa i logarytm dziesiętny, w rezultacie mamy .

d) Przechodzimy od dzielenia ułamków do mnożenia, zastępując ułamek dzielnik jego ułamkiem odwrotnym. Więc

Licznik powstałego ułamka można przedstawić jako , z którego wyraźnie widać wspólny czynnik licznika i mianownika - współczynnik x, możesz przez niego zmniejszyć ułamek:

Odpowiedź:

a) , b) , V) , G) .

Należy pamiętać, że operacje na ułamkach zwykłych przeprowadza się z uwzględnieniem kolejności wykonywania czynności: najpierw mnożenie i dzielenie, następnie dodawanie i odejmowanie, a jeśli są nawiasy, to w pierwszej kolejności wykonywane są czynności w nawiasach.

Przykład.

Zrób coś z ułamkami .

Rozwiązanie.

Najpierw dodajemy ułamki w nawiasach, po czym mnożymy:

Odpowiedź:

W tym miejscu pozostaje powiedzieć głośno trzy dość oczywiste, ale jednocześnie ważne punkty:

Konwersja wyrażeń za pomocą właściwości logarytmów

Najczęściej przekształcanie wyrażeń za pomocą logarytmów wiąże się z wykorzystaniem tożsamości wyrażających definicję logarytmu i

Naddniestrzański Uniwersytet Państwowy

ich. T.G. Szewczenko

Wydział Fizyki i Matematyki

Katedra Analizy Matematycznej

i metody nauczania matematyki

PRACA KURSOWA

„Przemiany tożsamości

wykładniczy i logarytmiczny

wyrażenia"

Prace ukończone:

uczeń grupy _______

Wydział Fizyki i Matematyki

_________________________

Sprawdziłem pracę:

_________________________

Tyraspol, 2003

Wprowadzenie…………………………………………………………………………2

Rozdział 1. Identyczne przekształcenia i metody nauczania w szkolnym toku algebry i na początku analizy……………………………………..4

§1. Kształcenie umiejętności stosowania określonych typów przekształceń……………………………………………………………………………………….4

§2. Cechy organizacji systemu wiedzy w badaniu przemian tożsamości.…….………………………….………..………….5

§3. Program matematyczny……………………………………………………….11

Rozdział 2. Identyczne przekształcenia i obliczenia wyrażeń wykładniczych i logarytmicznych……………………………...…………………13

§1. Uogólnienie pojęcia stopnia…………………………………..13

§2. Funkcja wykładnicza…………………………………………………..15

§3. Funkcja logarytmiczna………………………………….16

Rozdział 3. Identyczne przekształcenia wyrażeń wykładniczych i logarytmicznych w praktyce..........................................................................19

Zakończenie………………………………………………………..24

Lista referencji……………………………………………………….25
Wstęp

W ramach zajęć zostaną rozważone identyczne przekształcenia funkcji wykładniczej i logarytmicznej, rozważona zostanie metodologia ich nauczania na szkolnym kursie algebry i początek analizy.

W pierwszym rozdziale tej pracy opisano metodologię nauczania przekształceń tożsamości na szkolnym kursie matematyki, a także uwzględniono program matematyki w ramach kursu „Algebra i początki analizy” z badaniem funkcji wykładniczych i logarytmicznych.

Rozdział drugi bezpośrednio bada same funkcje wykładnicze i logarytmiczne, ich podstawowe właściwości wykorzystywane w przekształceniach tożsamości.

Rozdział trzeci poświęcony jest rozwiązywaniu przykładów i problemów przy użyciu identycznych transformacji funkcji wykładniczej i logarytmicznej.

Nauka różnych przekształceń wyrażeń i wzorów zajmuje znaczną część czasu dydaktycznego na szkolnych zajęciach z matematyki. Najprostsze przekształcenia, bazujące na własnościach działań arytmetycznych, przeprowadza się już w szkole podstawowej oraz w klasach IV-V. Jednak główny ciężar rozwijania umiejętności i zdolności do przeprowadzania przekształceń spoczywa na szkolnym kursie algebry. Wynika to zarówno z gwałtownego wzrostu liczby i różnorodności przeprowadzanych przekształceń, jak i ze skomplikowania działań zmierzających do ich uzasadnienia i wyjaśnienia warunków stosowalności, identyfikacji i badania uogólnionych koncepcji tożsamości, transformacji identycznych, transformacja równoważna, konsekwencja logiczna.

Kultura dokonywania przekształceń tożsamości rozwija się podobnie jak kultura obliczeń, w oparciu o solidną wiedzę o własnościach operacji na obiektach (liczbach, wektorach, wielomianach itp.) i algorytmach ich realizacji. Przejawia się to nie tylko w umiejętności prawidłowego uzasadnienia przekształceń, ale także w umiejętności znalezienia najkrótszej drogi przejścia od pierwotnego wyrażenia analitycznego do wyrażenia najbardziej odpowiadającego celowi przekształcenia, w umiejętności monitorowania zmian dziedzina definicji wyrażeń analitycznych w łańcuchu identycznych przekształceń, szybkość i dokładność wykonywania przekształceń.

Istotnym problemem w nauczaniu matematyki jest zapewnienie wysokiej kultury obliczeń i przekształceń tożsamości. Jednak problem ten jest nadal daleki od zadowalającego rozwiązania. Dowodem na to są dane statystyczne publicznych władz oświatowych, które corocznie odnotowują błędy i nieracjonalne metody obliczeń oraz przekształcenia dokonywane przez uczniów różnych klas podczas wykonywania sprawdzianów. Potwierdzają to opinie uczelni wyższych na temat jakości wiedzy i umiejętności matematycznych kandydatów. Nie sposób nie zgodzić się z wnioskami władz oświatowych i uczelni, że niewystarczająco wysoki poziom kultury obliczeń i identycznych przekształceń w szkole średniej jest konsekwencją formalizmu w wiedzy uczniów, oddzielenia teorii od praktyki.

Rozdział 1.

Identyczne przekształcenia i metody nauczania

w szkolnym kursie algebry i na początku analizy.

§1. Kształtowanie umiejętności stosowania

specyficzne rodzaje transformacjitytuły.

System technik i zasad przeprowadzania przekształceń, stosowany na etapie rozpoczynania algebry, ma bardzo szerokie zastosowanie: wykorzystuje się go w studiowaniu całego kursu matematyki. Jednak właśnie ze względu na małą specyficzność system ten wymaga dodatkowych przekształceń uwzględniających cechy strukturalne przekształcanych wyrażeń oraz właściwości nowo wprowadzanych operacji i funkcji. Opanowanie odpowiednich typów przekształceń rozpoczyna się od wprowadzenia skróconych wzorów mnożenia. Następnie rozważane są przekształcenia związane z działaniem potęgowania z różnymi klasami funkcji elementarnych – wykładniczą, potęgową, logarytmiczną, trygonometryczną. Każda z tego typu przemian przechodzi przez fazę uczenia się, w której uwaga skupia się na opanowaniu ich charakterystycznych cech.

W miarę gromadzenia się materiału możliwe staje się uwydatnienie cech wspólnych wszystkich rozpatrywanych przekształceń i na tej podstawie wprowadzenie pojęć przekształceń identycznych i równoważnych.

Należy zauważyć, że koncepcja transformacji tożsamości jest podawana na szkolnym kursie algebry nie w pełnej ogólności, ale jedynie w zastosowaniu do wyrażeń. Transformacje dzielą się na dwie klasy: przekształcenia identyczne to przekształcenia wyrażeń, a przekształcenia równoważne to przekształcenia formuł. W przypadku konieczności uproszczenia jednej części wzoru, w tym wzorze podświetlane jest wyrażenie, które stanowi argument za zastosowaną transformacją tożsamości. Odpowiedni predykat uważa się za niezmieniony.

W sprawie organizowanie całościowego systemu przekształceń(synteza), to jego głównym celem jest utworzenie elastycznego i potężnego; aparatura odpowiednia do stosowania w rozwiązywaniu różnorodnych zadań edukacyjnych.

W trakcie algebry i na początku analizy holistyczny system przekształceń, już ukształtowany w swoich głównych cechach, jest stopniowo udoskonalany. Dodawane są do niego także pewne nowe rodzaje transformacji, które jednak jedynie go wzbogacają, rozszerzają jego możliwości, ale nie zmieniają jego struktury. Metodologia badania tych nowych przekształceń praktycznie nie różni się od tej stosowanej na kursie algebry.

§2. Cechy organizacjisystemy zadaniowe

podczas badania przemian tożsamości.

Podstawową zasadą organizacji dowolnego systemu zadań jest przedstawienie ich od prostych do złożonych, biorąc pod uwagę potrzebę pokonywania przez uczniów realnych trudności i tworzenia sytuacji problematycznych. Ta podstawowa zasada wymaga określenia cech tego materiału edukacyjnego. Do opisu różnych układów zadań w metodach matematycznych używa się pojęcia cykl ćwiczeń. Cykl ćwiczeń charakteryzuje się połączeniem w sekwencji ćwiczeń kilku aspektów studiowania i technik uporządkowania materiału. W odniesieniu do przekształceń tożsamości ideę cyklu można przedstawić następująco.

Cykl ćwiczeń związany jest z badaniem jednej tożsamości, wokół której grupują się inne tożsamości pozostające z nią w naturalnym związku. Cykl, obok wykonawczych, obejmuje zadania wymagające uznania stosowalności danej tożsamości. Badana tożsamość służy do przeprowadzania obliczeń w różnych dziedzinach liczbowych. Uwzględnia się specyfikę tożsamości; w szczególności zorganizowane są związane z nim figury retoryczne.

Zadania w każdym cyklu podzielone są na dwie grupy. Do pierwszej zaliczają się zadania realizowane w trakcie wstępnego zaznajamiania się z tożsamością. Stanowią materiał edukacyjny na kilka kolejnych lekcji połączonych jednym tematem. Druga grupa ćwiczeń łączy badaną tożsamość z różnymi zastosowaniami. Grupa ta nie tworzy jedności kompozycyjnej - ćwiczenia tutaj są rozproszone na różne tematy.

Opisana struktura cyklu odnosi się do etapu rozwijania umiejętności stosowania określonych typów przekształceń. W końcowym etapie - etapie syntezy, cykle ulegają modyfikacji. Po pierwsze, obie grupy zadań łączy się w „rozszerzony” cykl, a z pierwszej grupy wyłącza się te najprostsze pod względem treściowym lub złożoności wykonania zadania. Pozostałe rodzaje zadań stają się bardziej złożone. Po drugie, następuje przenikanie cykli związanych z różnymi tożsamościami, przez co zwiększa się rola działań mających na celu rozpoznanie stosowalności określonej tożsamości.

Zwróćmy uwagę na cechy cykli zadań związane z tożsamościami dla funkcji elementarnych. Cechy te wynikają z faktu, że po pierwsze, odpowiadające im tożsamości są badane w związku z badaniem materiału funkcjonalnego, a po drugie, pojawiają się później niż tożsamości pierwszej grupy i są badane przy użyciu już ukształtowanych umiejętności przeprowadzania transformacji tożsamości .

Każda nowo wprowadzona funkcja elementarna radykalnie poszerza zakres liczb, które można indywidualnie wyznaczać i nazywać. Dlatego w pierwszej grupie zadań cyklicznych powinny znaleźć się zadania polegające na ustaleniu powiązań pomiędzy tymi nowymi dziedzinami liczbowymi a pierwotną dziedziną liczb wymiernych. Podajmy przykłady takich zadań.

Przykład 1 . Obliczać:

Przy każdym wyrażeniu wskazana jest tożsamość, w cyklach, dla których mogą występować proponowane zadania. Celem takich zadań jest opanowanie cech zapisów, w tym symboli nowych operacji i funkcji, a także rozwinięcie umiejętności mowy matematycznej.

Znacząca część zastosowań przekształceń tożsamościowych związanych z funkcjami elementarnymi polega na rozwiązywaniu równań niewymiernych i transcendentalnych. Cykle związane z asymilacją tożsamości obejmują jedynie najprostsze równania, jednak tutaj wskazane jest przeprowadzenie pracy nad opanowaniem metody rozwiązywania takich równań: zmniejszenie jej poprzez zastąpienie niewiadomej równaniem algebraicznym.

Kolejność kroków dla tego rozwiązania jest następująca:

a) znajdź funkcję, dla której to równanie można przedstawić w postaci;

b) dokonać podstawienia i rozwiązać równanie;

c) rozwiązać każde z równań, gdzie jest zbiorem pierwiastków równania.

W przypadku stosowania opisanej metody krok b) jest często wykonywany w sposób dorozumiany, bez wprowadzania zapisu dla . Ponadto uczniowie często wolą spośród różnych ścieżek prowadzących do znalezienia odpowiedzi wybrać tę, która szybciej i łatwiej prowadzi do równania algebraicznego.

Przykład 2 . Rozwiąż równanie.

Pierwszy sposób:

Drugi sposób:

Tutaj widać, że w przypadku pierwszej metody krok a) jest trudniejszy niż w przypadku drugiej. Pierwsza metoda jest „trudniejsza na początek”, chociaż dalszy przebieg rozwiązania jest znacznie prostszy. Natomiast druga metoda ma tę zaletę, że charakteryzuje się większą łatwością i większą precyzją w uczeniu się redukcji do równania algebraicznego.

W przypadku szkolnego kursu algebry typowe są zadania, w których przejście do równania algebraicznego jest jeszcze prostsze niż w tym przykładzie. Główny ciężar takich zadań wiąże się z identyfikacją kroku c) jako niezależnej części procesu rozwiązania związanego z wykorzystaniem właściwości badanej funkcji elementarnej.

Przykład 3 . Rozwiąż równanie:

Równania te sprowadzają się do równań: a) lub ; b) lub . Do rozwiązania tych równań wymagana jest znajomość jedynie najprostszych faktów dotyczących funkcji wykładniczej: jej monotoniczności, zakresu wartości. Podobnie jak w poprzednim przykładzie, równania a) i b) można zaliczyć do pierwszej grupy z serii ćwiczeń rozwiązywania równań kwadratowych wykładniczych.

Dochodzimy zatem do klasyfikacji zadań w cyklach związanych z rozwiązywaniem równań przestępnych zawierających funkcję wykładniczą:

1) równania, które sprowadzają się do równań postaci i mają prostą, ogólną odpowiedź: ;

2) równania sprowadzające się do równań , gdzie jest liczbą całkowitą, lub , gdzie ;

3) równania sprowadzające się do równań i wymagające jednoznacznej analizy formy, w jakiej zapisano liczbę .

Podobnie można klasyfikować zadania dla innych funkcji elementarnych.

Znaczna część tożsamości badanych na kursach algebry i algebry oraz zasad analizy jest w nich udowadniana lub przynajmniej wyjaśniana. Ten aspekt badania tożsamości ma ogromne znaczenie dla obu kursów, ponieważ rozumowanie dowodowe jest w nich prowadzone z największą jasnością i rygorystycznością właśnie w odniesieniu do tożsamości. Poza tym materiałem dowody są zwykle mniej kompletne; nie zawsze można je odróżnić od użytego uzasadnienia.

Właściwości operacji arytmetycznych służą jako podstawa, na której budowane są dowody tożsamości.

Edukacyjny wpływ obliczeń i identycznych przekształceń może być ukierunkowany na rozwój logicznego myślenia, jeśli tylko uczniowie będą systematycznie zobowiązani do uzasadniania obliczeń i identycznych przekształceń, a także na rozwój myślenia funkcjonalnego, co osiąga się na różne sposoby. Znaczenie kalkulacji i identycznych przemian w rozwoju woli, pamięci, inteligencji, samokontroli i inicjatywy twórczej jest dość oczywiste.

Wymogi codziennej i przemysłowej praktyki obliczeniowej wymagają od studentów rozwinięcia silnych, zautomatyzowanych umiejętności racjonalnych obliczeń i transformacji tożsamości. Umiejętności te rozwijane są w trakcie dowolnej pracy obliczeniowej, jednak konieczne jest specjalne ćwiczenie szkoleniowe w zakresie szybkich obliczeń i transformacji.

Jeśli więc lekcja polega na rozwiązywaniu równań logarytmicznych z wykorzystaniem podstawowej tożsamości logarytmicznej, warto uwzględnić w planie lekcji ustne ćwiczenia dotyczące upraszczania lub obliczania znaczeń wyrażeń: , , . Cel ćwiczeń jest zawsze komunikowany studentom. W trakcie ćwiczenia może zaistnieć potrzeba wymagania od uczniów uzasadnienia poszczególnych przekształceń, działań lub rozwiązania całego problemu, nawet jeśli nie było to zaplanowane. Tam, gdzie możliwe są różne sposoby rozwiązania problemu, warto zawsze zadawać pytania: „Jak problem został rozwiązany?”, „Kto rozwiązał problem w inny sposób?”

Pojęcia tożsamości i transformacji tożsamości są wyraźnie wprowadzone na kursie algebry w klasie VI. Sama definicja identycznych wyrażeń nie może być w praktyce wykorzystana do udowodnienia identyczności dwóch wyrażeń, a zrozumieć, że istotą identycznych przekształceń jest zastosowanie do wyrażenia definicji i właściwości tych działań, które są wskazane w wyrażeniu, lub dodanie do jest to wyrażenie identyczne równe 0 lub pomnożone przez wyrażenie identycznie równe jeden. Ale nawet po opanowaniu tych przepisów uczniowie często nie rozumieją, dlaczego te przekształcenia pozwalają nam stwierdzić, że wyrażenia oryginalne i powstałe są identyczne, tj. przyjmuj te same wartości dla dowolnych systemów (zestawów) wartości zmiennych.

Ważne jest również, aby uczniowie jasno zrozumieli, że takie wnioski z identycznych przekształceń są konsekwencjami definicji i właściwości odpowiednich działań.

Nabyty w latach ubiegłych aparat przekształceń tożsamości zostaje rozbudowany w klasie VI. Rozszerzenie to rozpoczyna się od wprowadzenia tożsamości wyrażającej własność iloczynu potęg o tych samych podstawach: , gdzie , są liczbami całkowitymi.

§3. Program matematyczny.

W ramach zajęć szkolnych „Algebra i początki analizy” uczniowie systematycznie studiują funkcje wykładnicze i logarytmiczne oraz ich własności, identyczne przekształcenia wyrażeń logarytmicznych i wykładniczych oraz ich zastosowanie do rozwiązywania odpowiednich równań i nierówności, a także zapoznają się z podstawowymi pojęciami i stwierdzeniami .

W 11. klasie lekcje algebry trwają 3 godziny tygodniowo, łącznie 102 godziny w roku. Program zajmuje 36 godzin na badanie funkcji wykładniczych, logarytmicznych i potęgowych.

Program obejmuje rozważenie i zbadanie następujących zagadnień:

Pojęcie stopnia z wykładnikiem racjonalnym. Rozwiązywanie równań niewymiernych. Funkcja wykładnicza, jej własności i wykres. Identyczne przekształcenia wyrażeń wykładniczych. Rozwiązywanie równań i nierówności wykładniczych. Logarytm liczby. Podstawowe własności logarytmów. Funkcja logarytmiczna, jej własności i wykres. Rozwiązywanie równań i nierówności logarytmicznych. Pochodna funkcji wykładniczej. Liczba i logarytm naturalny. Pochodna funkcji potęgowej.

Głównym celem działu poświęconego funkcjom wykładniczym i logarytmicznym jest zapoznanie studentów z funkcjami wykładniczymi, logarytmicznymi i potęgowymi; uczyć studentów rozwiązywania równań wykładniczych i logarytmicznych oraz nierówności.

Pojęcia pierwiastka i stopnia z wykładnikiem wymiernym są uogólnieniem pojęć pierwiastka kwadratowego i stopnia z wykładnikiem całkowitym. Studenci powinni zwrócić uwagę, że rozważane tutaj właściwości pierwiastków i potęg o wykładnikach wymiernych są podobne do właściwości, jakie posiadają badane wcześniej pierwiastki kwadratowe i potęgi o wykładnikach całkowitych. Należy poświęcić odpowiednią ilość czasu na ćwiczenie właściwości stopni i rozwijanie umiejętności transformacji tożsamości. Pojęcie stopnia z irracjonalnym wykładnikiem jest wprowadzone w sposób wizualny i intuicyjny. Materiał ten pełni rolę pomocniczą i jest używany przy wprowadzaniu funkcji wykładniczej.

Badanie właściwości funkcji wykładniczych, logarytmicznych i potęgowych jest skonstruowane zgodnie z przyjętym ogólnym schematem badania funkcji. W tym przypadku następuje przegląd właściwości w zależności od wartości parametrów. Nierówności wykładnicze i logarytmiczne rozwiązuje się w oparciu o badane właściwości funkcji.

Cechą charakterystyczną kursu jest systematyzacja i uogólnianie wiedzy studentów, utrwalanie i rozwijanie umiejętności nabytych na kursie algebry, co odbywa się zarówno podczas studiowania nowego materiału, jak i podczas wykonywania uogólnionych powtórek.
Rozdział 2.

Transformacje i obliczenia tożsamościowe

wyrażenia wykładnicze i logarytmiczne

§1. Uogólnienie pojęcia stopnia.

Definicja: Pierwiastek th z czystej liczby to liczba, której th potęga jest równa .

Zgodnie z tą definicją rozwiązaniem równania jest pierwiastek z liczby. Liczba pierwiastków tego równania zależy od i. Rozważmy funkcję. Jak wiadomo, na przedziale funkcja ta zwiększa się dla dowolnej wartości i pobiera wszystkie wartości z przedziału. Zgodnie z twierdzeniem o pierwiastku równanie dla dowolnego ma pierwiastek nieujemny, a ponadto tylko jeden. Wzywają go pierwiastek arytmetyczny z th stopnia liczby i oznaczać ; numer jest wywoływany indeks główny, a sama liczba jest radykalne wyrażenie. Znak nazywany jest również radykałem.

Definicja: Pierwiastek arytmetyczny z potęgi liczby jest liczbą nieujemną, której -ta potęga jest równa .

Dla liczb parzystych funkcja jest parzysta. Wynika z tego, że jeśli , to równanie oprócz pierwiastka ma również pierwiastek. Jeśli , to istnieje jeden pierwiastek: ; jeśli , to równanie nie ma pierwiastków, ponieważ potęga parzysta dowolnej liczby jest nieujemna.

W przypadku wartości nieparzystych funkcja rośnie wzdłuż całej osi liczbowej; jego zakres to zbiór wszystkich liczb rzeczywistych. Stosując twierdzenie o pierwiastku, stwierdzamy, że równanie ma jeden pierwiastek dla dowolnego, a w szczególności dla . Ten pierwiastek dla dowolnej wartości jest oznaczony przez .

Dla pierwiastków stopnia nieparzystego równość jest prawdziwa. Faktycznie, tj. liczba jest pierwiastkiem th. Ale taki pierwiastek dla nieparzystego jest jedyny. Stąd, .

Uwaga 1: Dla każdego prawdziwego

Przypomnijmy znane właściwości pierwiastków arytmetycznych stopnia VII.

Dla dowolnej liczby naturalnej obowiązują liczby całkowite i dowolne nieujemne liczby całkowite oraz równości:

Stopień z wykładnikiem racjonalnym.

Wyrażenie jest zdefiniowane dla wszystkich z wyjątkiem przypadku w . Przypomnijmy właściwości takich mocy.

Dla dowolnych liczb i dowolnych liczb całkowitych oraz równości są ważne:

Zauważamy również, że jeśli , to w i na .

Definicja: Potęga liczby o wykładniku wymiernym, gdzie jest liczbą całkowitą, a jest liczbą naturalną, nazywana jest liczbą.

A więc z definicji.

Przy sformułowanej definicji stopnia z wykładnikiem wymiernym zostają zachowane podstawowe własności stopni, które są prawdziwe dla dowolnych wykładników (z tą różnicą, że własności te są prawdziwe tylko dla podstaw dodatnich).

§2. Funkcja wykładnicza.

Definicja: Nazywa się funkcję podaną wzorem (gdzie , ). funkcja wykładnicza o podstawie .

Sformułujmy główne właściwości funkcji wykładniczej.

Wykres funkcji (ryc. 1)

Formuły te nazywane są podstawowe właściwości stopni.

Można także zauważyć, że funkcja jest ciągła na zbiorze liczb rzeczywistych.

§3. Funkcja logarytmiczna.

Definicja: Logarytm liczby do podstawy nazywa się wykładnikiem, do którego należy podnieść podstawę. Aby uzyskać numer.

Formuła (gdzie , i ) jest wywoływana podstawowa tożsamość logarytmiczna.

Podczas pracy z logarytmami wykorzystuje się następujące właściwości, wynikające z właściwości funkcji wykładniczej:

Dla każdego( )i wszystkie dodatnie i równości są spełnione:

5. dla każdego prawdziwego .

Podstawowe właściwości logarytmów są szeroko stosowane przy konwersji wyrażeń zawierających logarytmy. Na przykład często stosuje się wzór na przejście z jednej podstawy logarytmu na drugą: .

Niech będzie liczbą dodatnią różną od 1.

Definicja: Funkcja podana we wzorze nazywa się funkcja logarytmiczna o podstawie.

Wymieńmy główne właściwości funkcji logarytmicznej.

1. Dziedziną definicji funkcji logarytmicznej jest zbiór wszystkich liczb dodatnich, tj. .

2. Zakres wartości funkcji logarytmicznej to zbiór wszystkich liczb rzeczywistych.

3. Funkcja logarytmiczna rośnie (at ) lub maleje (at ) w całym obszarze definicji.

Wykres funkcji (ryc. 2)

Wykresy funkcji wykładniczych i logarytmicznych o tej samej podstawie są symetryczne względem prostej(ryc. 3).

Rozdział 3.

Identyczne transformacje wykładnicze i

wyrażenia logarytmiczne w praktyce.

Zadanie 1.

Obliczać:

Rozwiązanie:

Odpowiedź:; ; ; ; .; , rozumiemy to

Studiując ten materiał, rozważałem metody rozwijania umiejętności uczniów. Przedstawiła także program z matematyki do badania przebiegu funkcji wykładniczych i logarytmicznych na kursie „Algebra i początek analizy”.

W pracy przedstawiono zadania o różnej złożoności i treści, stosując identyczne przekształcenia. Zadania te można wykorzystać do przeprowadzenia testów lub samodzielnej pracy sprawdzającej wiedzę uczniów.

Praca kursowa, moim zdaniem, została zrealizowana w ramach metodologii nauczania matematyki w szkołach średnich i może służyć jako pomoc wizualna dla nauczycieli szkolnych, a także dla studentów studiów stacjonarnych i niestacjonarnych.

Lista wykorzystanej literatury:

1. Algebra i początki analizy. wyd. Kołmogorowa A.N. M.: Edukacja, 1991.
2. Program dla szkół średnich, gimnazjów, liceów. Matematyka 5-11 klas. M.: Drop, 2002.
3. JEŚLI. Sharygin, V.I. Gołubiew. Opcjonalny kurs matematyki (rozwiązywanie problemów). Uch. dodatek dla klasy 11. M.: Edukacja, 1991.
4. VA Oganesyan i in. Metody nauczania matematyki w szkole średniej: Metody ogólne; Podręcznik dla studentów Wydziału Fizyki i Matematyki Instytutów Pedagogicznych. -Wydanie drugie poprawione i rozszerzone M.: Edukacja, 1980.
5. Czerkasow R.S., Stolyar A.A. Metody nauczania matematyki w szkole średniej. M.: Edukacja, 1985.
6. Magazyn „Matematyka w szkole”.

EGOROWA WIKTORIA WALERIEWNA

Nauczyciel matematyki

najwyższa kategoria kwalifikacji

TEMAT: „Transformacja IDENTALNA

WYRAŻENIA LOGARYTMICZNE”

Wiedza i umiejętności, które uczniowie powinni opanować po przestudiowaniu tej lekcji:

znać definicję logarytmu liczby, podstawową tożsamość logarytmiczną, własności logarytmów;

potrafić dokonywać przekształceń wyrażeń zawierających logarytmy i obliczać logarytmy.

Literatura:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. i inne Algebra i początki analizy: podręcznik dla klas 10-11 w szkołach ogólnokształcących. – M.: Edukacja, 2001.

2. Kochagin V.V., Kochagina M.V., Intensywny kurs przygotowujący do jednolitego egzaminu państwowego. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Symulator algebraiczny: podręcznik dla uczniów i kandydatów. – M.: Ilexa, 2005.

4. Gusiew V.A., Mordkovich A.G. Matematyka: Literatura: Książka dla studentów. – M.: Edukacja, 2001.

Plan lekcji:

Postęp lekcji:

1) Logarytm to greckie słowo składające się z 2 słów: „logos” – stosunek, „arithmos” – liczba. Oznacza to, że logarytm jest liczbą mierzącą stosunek. W publikacji z 1614 r. podano, że Napier wynalazł logarytmy. Później skompilował tablice logarytmiczne, które obecnie są nam znane jako tablice Bradisa. W ciągu niecałego stulecia stoły rozprzestrzeniły się na całym świecie i stały się niezbędnym narzędziem obliczeniowym. Następnie zostały one niejako wbudowane w wygodne urządzenie, które znacznie przyspiesza proces obliczeń – suwak logarytmiczny, który był używany do lat siedemdziesiątych XX wieku.

Załącznik 1.

2) Logarytm liczba dodatniaB na podstawie A, I i jest większa od zera i różna od jedności,jest wykładnikiem, do którego należy podnieść liczbęA aby uzyskać numerB.

Nazywa się tę równość, wyrażającą definicję logarytmupodstawowa tożsamość logarytmiczna .

C

LUB 1

P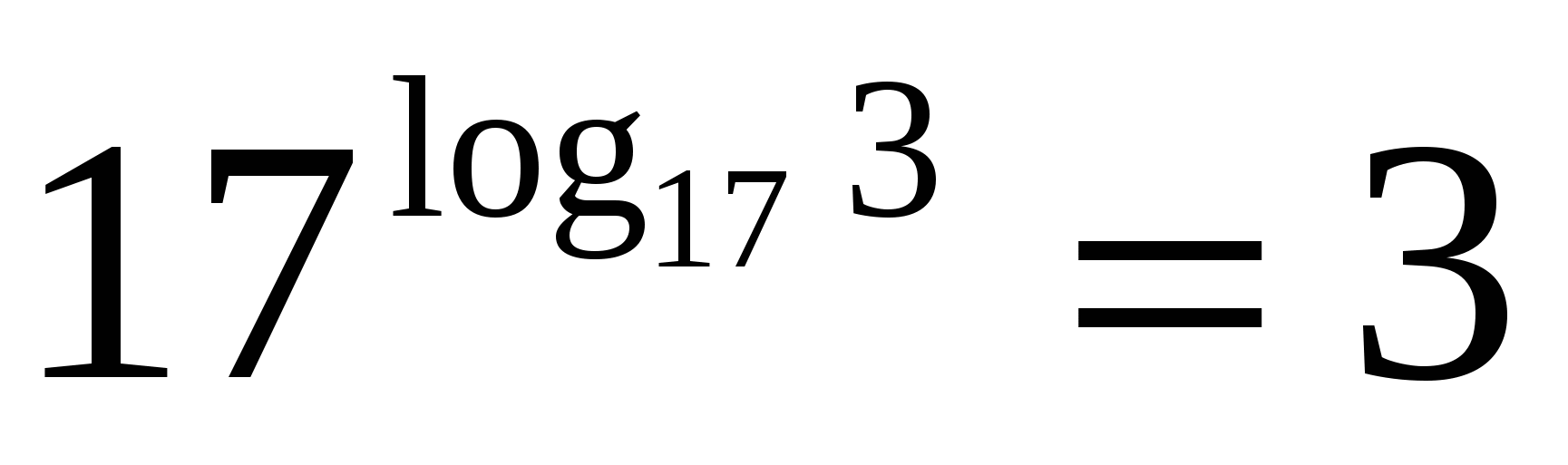

Podstawą potęgi i podstawą logarytmu jest siedemnaście, co oznacza, że ​​zgodnie z podstawową tożsamością logarytmiczną wartość wyrażenia wynosi trzy.

Przepracujmy to ustnie:

SCH
FIR-BELLE

O dolna część sekundy jest równa zero przecinek pięć, co oznacza, że ​​wyrażenie jest równe arytmetycznemu pierwiastkowi kwadratowemu z pięciu.

P

Dodatek 2.

Równość to znaczy

Z definicji logarytmu wynikają następujące ważne równości:

Na przykład:

P
Dodatek 3.

Przejdźmy do zadań egzaminu Unified State Exam:

Dodatek 4.

3
) Istnieje specjalny zapis i nazwa logarytmu dziesiętnegologarytm dziesiętny .

L
kalarytm podstawowymi zwanylogarytm naturalny .

N
Na przykład,

4) Z definicji logarytmu wynikają następujące właściwości. Wszystkie właściwości są formułowane i udowadniane tylko dla dodatnich wartości zmiennych zawartych pod znakami logarytmów.

Logarytm iloczynu dwóch liczb dodatnich do podstawy A równa sumie logarytmów tych liczb o tej samej podstawie.

TsOR 2

Na przykład,

Z
zadanie 1.

Zadanie 2. Uprość wyrażenie

W
Skorzystajmy z rozwiązania z poprzedniego przykładu. Wymienimy

Należy pamiętać, że logarytm jest kwadratowy, więc suma musi być kwadratowa. Korzystając ze wzoru na kwadrat sumy, otwieramy nawiasy. Przedstawmy podobne określenia.

5) Logarytm ilorazu jest równy różnicy między logarytmami dywidendy i dzielnika.

C

Zwróć uwagę na podstawę potęgi i podstawę logarytmu - są takie same.

LUB 3

R

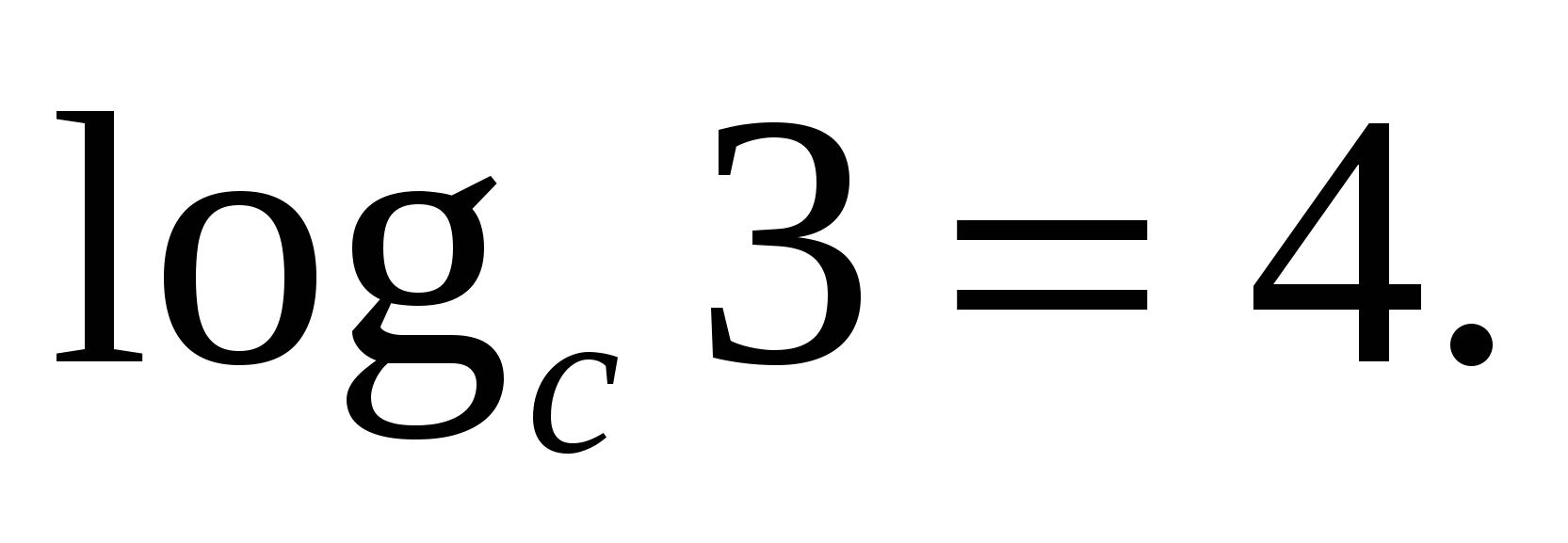Przyjrzyjmy się zastosowaniu tej formuły na przykładzie:

Z
zadanie 1. Znajdź wartość wyrażenia jeśli

Zadanie 2. Znajdź wartość B według jego logarytmu

6) Logarytm potęgi o podstawieA , jest równy iloczynowi wykładnika i logarytmu o tej samej podstawie.

TsOR 4

Na przykład,

Z
zadanie 1. Oblicz, jeśli

Uprośćmy wyrażenie

Formuła

zwany formuła przejścia na nową bazę.

Z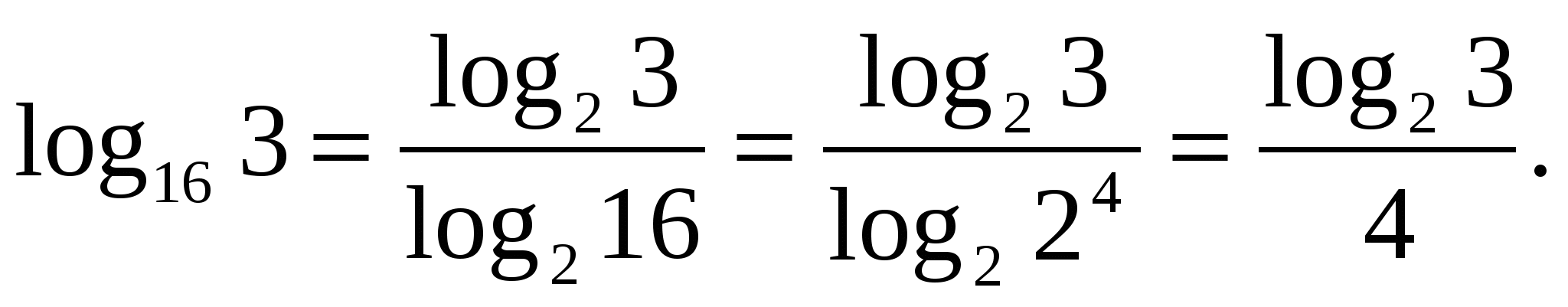

zadanie 1. Wyraź za pomocą logarytmu o podstawie 2.

Zadanie 2. Obliczać

TsOR 5

TSR 6

Na przykład,

Z

zadanie 1. Obliczać

Z
zadanie 2. Obliczać

9) Przekształcenia logarytmiczne można rozpocząć tylko w przypadkach, gdy jeśli pamiętasz wszystkie właściwości logarytmów. Po ich powtórzeniu rozważymy zadania transformacji wyrażeń logarytmicznych z drugiej strony.

Aby przeliczyć sumę lub różnicę wyrażeń logarytmicznych, czasami wystarczy skorzystać z definicji logarytmu, a najczęściej z właściwości logarytmu iloczynu lub ilorazu.

Z
zadanie 1. Obliczać

Rozwiążmy to na dwa sposoby.

1 sposób, korzystając z definicji logarytmu:

Metoda 2, oparta na właściwość logarytmu ilorazu:

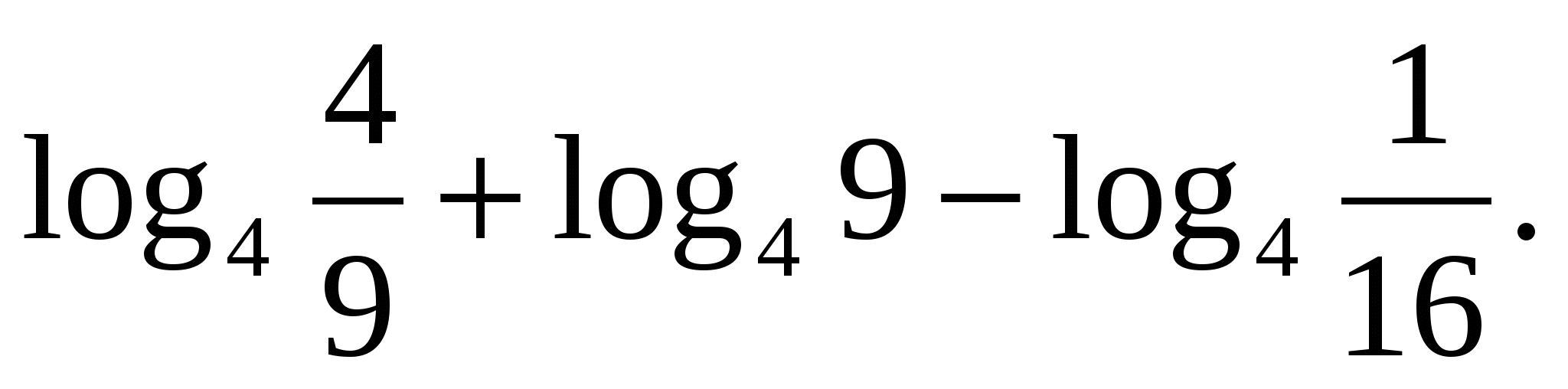
Zadanie 2. Znajdź znaczenie wyrażenia

Najpierw zastosujmy formułę logarytm iloczynu, a następnie definicja logarytmu.

Podstawowa tożsamość logarytmiczna jest używana podczas konwersji wyrażeń zawierających logarytm jako wykładnik. Ideą takich operacji jest uzyskanie równych podstaw potęg i podstaw logarytmu.

Czasami konieczne jest przekształcenie wyrażenia także przez właściwości logarytmu i właściwości stopnia możesz łatwo przechodzić z jednej bazy do drugiej, korzystając z formuły przejścia. W innych przypadkach należy zastosować wiele właściwości.

Z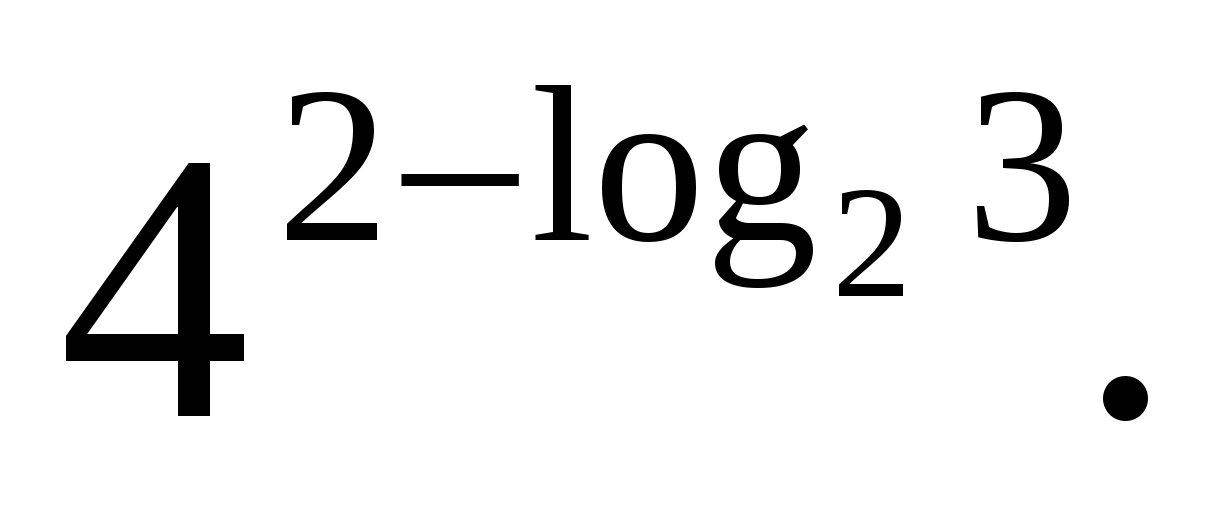
zadanie 3. Obliczać

Z
zadanie 4. Znajdź znaczenie wyrażenia

Zadanie 5. Znajdź znaczenie wyrażenia

Z
zadanie 6. Wyraź to jako różnicę logarytmów

N
Największą trudność stanowi konwersja wyrażeń logarytmicznych pod pierwiastek. W procesie transformacji należy wziąć pod uwagę moduły wyrażeń logarytmicznych, aby rozwiązać które z nich, należy porównać liczby niewymierne lub liczbę wymierną i niewymierną. Będziemy działać konsekwentnie. Przyjrzyjmy się wyrażeniu pod pierwiastkiem wewnętrznym.

Zastąpmy to oryginalnym wyrażeniem.

Należy zaznaczyć, że transformację wyrażeń logarytmicznych można spotkać także przy rozwiązywaniu równań i nierówności czy badaniu funkcji, dlatego mogą one występować w formie ukrytej w zadaniach grup B i C.

10) Podsumowując pytania:

Nazywa się logarytm o podstawie 10

podstawowy logarytm

logarytm główny

logarytm naturalny

logarytm dziesiętny

2) Jakie wartości może przyjmować?X w wyrazie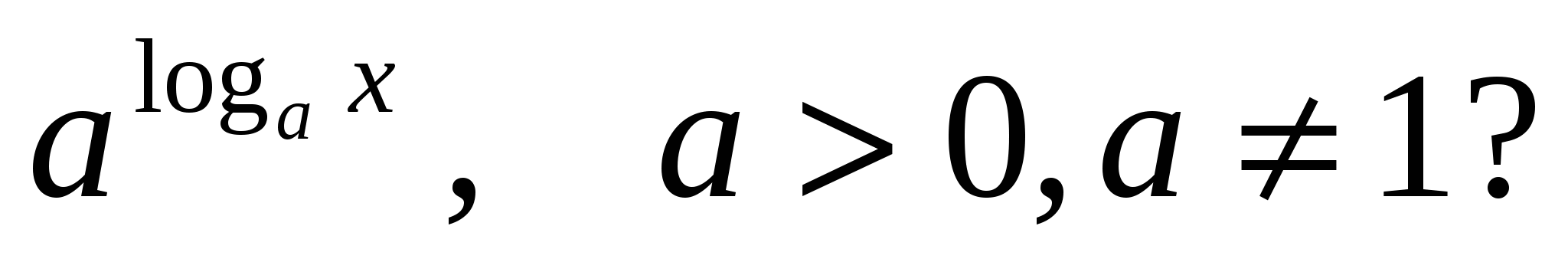

Wartość nie jest zdefiniowana

5) Podaj stosunek, który jest prawdziwy dla wszystkichX ≠ 0 .

6) Wskaż prawidłowy stosunek wzoru na przejście do nowej bazy.

7) Podaj poprawną równość dla

11) Testy kontrolne.

Przykład 1 . Obliczać:

Przy każdym wyrażeniu wskazana jest tożsamość, w cyklach, dla których mogą występować proponowane zadania. Celem takich zadań jest opanowanie cech zapisów, w tym symboli nowych operacji i funkcji, a także rozwinięcie umiejętności mowy matematycznej.

Znacząca część zastosowań przekształceń tożsamościowych związanych z funkcjami elementarnymi polega na rozwiązywaniu równań niewymiernych i transcendentalnych. Cykle związane z asymilacją tożsamości obejmują jedynie najprostsze równania, jednak tutaj wskazane jest przeprowadzenie pracy nad opanowaniem metody rozwiązywania takich równań: zmniejszenie jej poprzez zastąpienie niewiadomej równaniem algebraicznym.

Kolejność kroków dla tego rozwiązania jest następująca:

a) znajdź funkcję

, dla którego to równanie można przedstawić jako ;

b) dokonać zamiany

i rozwiązać równanie ;

c) rozwiązać każde z równań

, gdzie jest zbiorem pierwiastków równania .

Stosując opisaną metodę, krok b) często wykonuje się w sposób dorozumiany, bez wprowadzania zapisu dla

. Ponadto uczniowie często wolą spośród różnych ścieżek prowadzących do znalezienia odpowiedzi wybrać tę, która szybciej i łatwiej prowadzi do równania algebraicznego.

Przykład 2 . Rozwiąż równanie

.

Pierwszy sposób:

Drugi sposób:

Tutaj widać, że w przypadku pierwszej metody krok a) jest trudniejszy niż w przypadku drugiej. Pierwsza metoda jest „trudniejsza na początek”, chociaż dalszy przebieg rozwiązania jest znacznie prostszy. Natomiast druga metoda ma tę zaletę, że charakteryzuje się większą łatwością i większą precyzją w uczeniu się redukcji do równania algebraicznego.

W przypadku szkolnego kursu algebry typowe są zadania, w których przejście do równania algebraicznego jest jeszcze prostsze niż w tym przykładzie. Główny ciężar takich zadań wiąże się z identyfikacją kroku c) jako niezależnej części procesu rozwiązania związanego z wykorzystaniem właściwości badanej funkcji elementarnej.

Przykład 3 . Rozwiąż równanie:

; B) .

Równania te sprowadzają się do równań: a)

Lub ; b) lub . Do rozwiązania tych równań wymagana jest znajomość jedynie najprostszych faktów dotyczących funkcji wykładniczej: jej monotoniczności, zakresu wartości. Podobnie jak w poprzednim przykładzie, równania a) i b) można zaliczyć do pierwszej grupy z serii ćwiczeń rozwiązywania równań kwadratowych wykładniczych.

Dochodzimy zatem do klasyfikacji zadań w cyklach związanych z rozwiązywaniem równań przestępnych zawierających funkcję wykładniczą:

1) równania sprowadzające się do równań postaci

i mając prostą, ogólną odpowiedź: ;

2) równania sprowadzające się do równań

, gdzie jest liczbą całkowitą lub , gdzie ;

3) równania sprowadzające się do równań

i wymagające wyraźnej analizy formy, w jakiej zapisano liczbę .

Podobnie można klasyfikować zadania dla innych funkcji elementarnych.

Znaczna część tożsamości badanych na kursach algebry i algebry oraz zasad analizy jest w nich udowadniana lub przynajmniej wyjaśniana. Ten aspekt badania tożsamości ma ogromne znaczenie dla obu kursów, ponieważ rozumowanie dowodowe jest w nich prowadzone z największą jasnością i rygorystycznością właśnie w odniesieniu do tożsamości. Poza tym materiałem dowody są zwykle mniej kompletne; nie zawsze można je odróżnić od użytego uzasadnienia.

Właściwości operacji arytmetycznych służą jako podstawa, na której budowane są dowody tożsamości.

Edukacyjny wpływ obliczeń i identycznych przekształceń może być ukierunkowany na rozwój logicznego myślenia, jeśli tylko uczniowie będą systematycznie zobowiązani do uzasadniania obliczeń i identycznych przekształceń, a także na rozwój myślenia funkcjonalnego, co osiąga się na różne sposoby. Znaczenie kalkulacji i identycznych przemian w rozwoju woli, pamięci, inteligencji, samokontroli i inicjatywy twórczej jest dość oczywiste.

Wymogi codziennej i przemysłowej praktyki obliczeniowej wymagają od studentów rozwinięcia silnych, zautomatyzowanych umiejętności racjonalnych obliczeń i transformacji tożsamości. Umiejętności te rozwijane są w trakcie dowolnej pracy obliczeniowej, jednak konieczne jest specjalne ćwiczenie szkoleniowe w zakresie szybkich obliczeń i transformacji.

Tak więc, jeśli lekcja obejmuje rozwiązywanie równań logarytmicznych przy użyciu podstawowej tożsamości logarytmicznej

, wówczas warto uwzględnić w planie lekcji ćwiczenia ustne dotyczące upraszczania lub obliczania znaczeń wyrażeń: , , . Cel ćwiczeń jest zawsze komunikowany studentom. W trakcie ćwiczenia może zaistnieć potrzeba wymagania od uczniów uzasadnienia poszczególnych przekształceń, działań lub rozwiązania całego problemu, nawet jeśli nie było to zaplanowane. Tam, gdzie możliwe są różne sposoby rozwiązania problemu, warto zawsze zadawać pytania: „Jak problem został rozwiązany?”, „Kto rozwiązał problem w inny sposób?”

Pojęcia tożsamości i transformacji tożsamości są wyraźnie wprowadzone na kursie algebry w klasie VI. Sama definicja identycznych wyrażeń nie może być w praktyce wykorzystana do udowodnienia identyczności dwóch wyrażeń, a zrozumieć, że istotą identycznych przekształceń jest zastosowanie do wyrażenia definicji i właściwości tych działań, które są wskazane w wyrażeniu, lub dodanie do jest to wyrażenie identyczne równe 0 lub pomnożone przez wyrażenie identycznie równe jeden. Ale nawet po opanowaniu tych przepisów uczniowie często nie rozumieją, dlaczego te przekształcenia pozwalają nam stwierdzić, że wyrażenia oryginalne i powstałe są identyczne, tj. przyjmuj te same wartości dla dowolnych systemów (zestawów) wartości zmiennych.

Ważne jest również, aby uczniowie jasno zrozumieli, że takie wnioski z identycznych przekształceń są konsekwencjami definicji i właściwości odpowiednich działań.

Nabyty w latach ubiegłych aparat przekształceń tożsamości zostaje rozbudowany w klasie VI. Rozszerzenie to rozpoczyna się od wprowadzenia tożsamości wyrażającej własność iloczynu potęg o tych samych podstawach:

Pojęcie stopnia z wykładnikiem racjonalnym. Rozwiązywanie równań niewymiernych. Funkcja wykładnicza, jej własności i wykres. Identyczne przekształcenia wyrażeń wykładniczych. Rozwiązywanie równań i nierówności wykładniczych. Logarytm liczby. Podstawowe własności logarytmów. Funkcja logarytmiczna, jej własności i wykres. Rozwiązywanie równań i nierówności logarytmicznych. Pochodna funkcji wykładniczej. Liczba i logarytm naturalny. Pochodna funkcji potęgowej.

Głównym celem działu poświęconego funkcjom wykładniczym i logarytmicznym jest zapoznanie studentów z funkcjami wykładniczymi, logarytmicznymi i potęgowymi; uczyć studentów rozwiązywania równań wykładniczych i logarytmicznych oraz nierówności.

Pojęcia pierwiastka i stopnia z wykładnikiem wymiernym są uogólnieniem pojęć pierwiastka kwadratowego i stopnia z wykładnikiem całkowitym. Studenci powinni zwrócić uwagę, że rozważane tutaj właściwości pierwiastków i potęg o wykładnikach wymiernych są podobne do właściwości, jakie posiadają badane wcześniej pierwiastki kwadratowe i potęgi o wykładnikach całkowitych. Należy poświęcić odpowiednią ilość czasu na ćwiczenie właściwości stopni i rozwijanie umiejętności transformacji tożsamości. Pojęcie stopnia z irracjonalnym wykładnikiem jest wprowadzone w sposób wizualny i intuicyjny. Materiał ten pełni rolę pomocniczą i jest używany przy wprowadzaniu funkcji wykładniczej.

Badanie właściwości funkcji wykładniczych, logarytmicznych i potęgowych jest skonstruowane zgodnie z przyjętym ogólnym schematem badania funkcji. W tym przypadku następuje przegląd właściwości w zależności od wartości parametrów. Nierówności wykładnicze i logarytmiczne rozwiązuje się w oparciu o badane właściwości funkcji.

Cechą charakterystyczną kursu jest systematyzacja i uogólnianie wiedzy studentów, utrwalanie i rozwijanie umiejętności nabytych na kursie algebry, co odbywa się zarówno podczas studiowania nowego materiału, jak i podczas wykonywania uogólnionych powtórek.

Zadanie B7 daje pewne wyrażenie, które należy uprościć. Wynik powinien być liczbą, którą można zapisać na karcie odpowiedzi. Wszystkie wyrażenia są umownie podzielone na trzy typy:

1. logarytmiczny,
2. Orientacyjny,
3. Łączny.

Wyrażenia wykładnicze i logarytmiczne w czystej postaci praktycznie nigdy nie występują. Jednak wiedza o tym, jak są one obliczane, jest absolutnie konieczna.

Ogólnie rzecz biorąc, problem B7 rozwiązuje się po prostu i mieści się w możliwościach przeciętnego absolwenta. Brak przejrzystych algorytmów rekompensuje standaryzacja i monotonia. Rozwiązywania takich problemów można się nauczyć po prostu poprzez wiele szkoleń.

Wyrażenia logarytmiczne

Zdecydowana większość problemów B7 dotyczy logarytmów w takiej czy innej formie. Temat ten jest tradycyjnie uważany za trudny, ponieważ jego nauka odbywa się zwykle w 11. klasie - epoce masowego przygotowania do egzaminów końcowych. W rezultacie wielu absolwentów ma bardzo niejasne pojęcie o logarytmach.

Ale w tym zadaniu nikt nie wymaga głębokiej wiedzy teoretycznej. Spotkamy się tylko z najprostszymi wyrażeniami, które wymagają prostego rozumowania i które można łatwo opanować samodzielnie. Poniżej znajdują się podstawowe wzory, które musisz znać, aby radzić sobie z logarytmami:

Ponadto musisz umieć zastąpić pierwiastki i ułamki potęgami wykładnikiem wymiernym, w przeciwnym razie w niektórych wyrażeniach po prostu nie będzie nic do wyjęcia spod znaku logarytmu. Formuły zastępcze:

Zadanie. Znajdź znaczenie wyrażeń:
log 6 270 − log 6 7,5
log 5 775 − log 5 6.2

Pierwsze dwa wyrażenia są konwertowane jako różnica logarytmów:
log 6 270 - log 6 7,5 = log 6 (270: 7,5) = log 6 36 = 2;
log 5 775 - log 5 6,2 = log 5 (775: 6,2) = log 5 125 = 3.

Aby obliczyć trzecie wyrażenie, będziesz musiał wyodrębnić potęgi - zarówno w podstawie, jak i w argumencie. Najpierw znajdźmy logarytm wewnętrzny:

Następnie - zewnętrzne:

Konstrukcje postaci log a log b x wydają się skomplikowane i dla wielu niezrozumiałe. Tymczasem jest to tylko logarytm logarytmu, tj. log a (log b x ). Najpierw obliczany jest logarytm wewnętrzny (postawmy log b x = c), a następnie zewnętrzny: log a c.

Wyrażenia demonstracyjne

Wyrażeniem wykładniczym nazwiemy dowolną konstrukcję postaci a k, gdzie liczby a i k są dowolnymi stałymi, a a > 0. Metody pracy z takimi wyrażeniami są dość proste i omawiane są na lekcjach algebry w ósmej klasie.

Poniżej znajdują się podstawowe formuły, które na pewno musisz znać. Stosowanie tych formuł w praktyce z reguły nie sprawia problemów.

1. za n · za m = za n + m ;
2. za n / za m = za n - m ;
3. (za n) m = za n · m;
4. (a · b) n = za n · b n;
5. (a: b) n = za n: b n.

Jeśli natkniesz się na złożone wyrażenie z potęgami i nie wiesz, jak do niego podejść, zastosuj uniwersalną technikę - rozkład na proste czynniki. W rezultacie duże liczby w podstawach potęg zostają zastąpione prostymi i zrozumiałymi elementami. Następnie pozostaje tylko zastosować powyższe formuły - i problem zostanie rozwiązany.

Zadanie. Znajdź wartości wyrażeń: 7 9 · 3 11: 21 8, 24 7: 3 6: 16 5, 30 6: 6 5: 25 2.

Rozwiązanie. Rozłóżmy wszystkie podstawy potęg na proste czynniki:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150 .

Połączone zadania

Jeśli znasz formuły, wszystkie wyrażenia wykładnicze i logarytmiczne można rozwiązać dosłownie w jednym wierszu. Jednakże w zadaniu B7 potęgi i logarytmy można łączyć, tworząc całkiem mocne kombinacje.