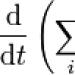تبدیلات یکسان عبارات حاوی توان و لگاریتم. عبارات لگاریتمی

اکنون تبدیل عبارات حاوی لگاریتم را از دیدگاه کلی بررسی خواهیم کرد. در اینجا نه تنها تبدیل عبارات را با استفاده از خواص لگاریتم بررسی می کنیم، بلکه تبدیل عبارات با لگاریتم های عمومی را نیز در نظر می گیریم که نه تنها شامل لگاریتم ها، بلکه توان ها، کسرها، ریشه ها و غیره هستند. طبق معمول، ما تمام مطالب را با نمونه های معمولی همراه با توضیحات دقیق راه حل ها ارائه خواهیم کرد.

پیمایش صفحه.

عبارات با لگاریتم و عبارات لگاریتمی

انجام کارها با کسرها

در پاراگراف قبل، تبدیل‌های اساسی را که با کسرهای منفرد حاوی لگاریتم انجام می‌شوند، بررسی کردیم. البته این تبدیل‌ها را می‌توان با هر کسر مجزا انجام داد که بخشی از عبارت پیچیده‌تر است، به عنوان مثال، مجموع، تفاوت، حاصلضرب و ضریب کسرهای مشابه را نشان می‌دهد. اما علاوه بر کار با کسرهای منفرد، تبدیل عبارات از این نوع اغلب شامل انجام عملیات متناظر با کسری است. در ادامه به قوانینی که توسط آنها این اقدامات انجام می شود نگاه خواهیم کرد.

از کلاس های پنجم تا ششم، قوانینی را که توسط آنها انجام می شود، می دانیم. در مقاله نگاهی کلی به عملیات با کسریما این قوانین را از کسرهای معمولی به کسری هایی با شکل کلی A/B گسترش داده ایم، که در آن A و B برخی از عبارات عددی، تحت اللفظی یا متغیر هستند و B به طور یکسان برابر با صفر نیست. واضح است که کسرهای دارای لگاریتم موارد خاصی از کسرهای عمومی هستند. و در این راستا مشخص است که عملیات با کسری که دارای لگاریتم در نمادهای خود است، طبق قوانین مشابه انجام می شود. برای مثال:

• برای جمع یا تفریق دو کسر با مخرج یکسان، باید اعداد را بر اساس آن جمع یا تفریق کنید، اما مخرج را ثابت بگذارید.
• برای جمع یا تفریق دو کسر با مخرج های مختلف، باید آنها را به یک مخرج مشترک بیاورید و طبق قانون قبلی اعمال مناسب را انجام دهید.
• برای ضرب دو کسر، باید کسری بنویسید که صورت آن حاصل ضرب کسرهای اصلی و مخرج حاصل ضرب مخرج ها باشد.
• برای تقسیم کسری به کسری، باید کسری را که تقسیم می‌شود در کسری که معکوس تقسیم‌کننده است ضرب کنید، یعنی در کسری که صورت و مخرج آن عوض شده است.

در اینجا چند نمونه از نحوه انجام عملیات با کسرهای حاوی لگاریتم آورده شده است.

مثال.

انجام عملیات با کسرهای حاوی لگاریتم: الف) ، ب) ، V) ، G) .

راه حل.

الف) مخرج کسری که اضافه می شود آشکارا یکسان است. بنابراین طبق قانون جمع کسری با مخرج یکسان، اعداد را جمع می کنیم و مخرج را ثابت می گذاریم: .

ب) در اینجا مخرج ها متفاوت است. بنابراین، ابتدا شما نیاز دارید کسرها را به مخرج یکسان تبدیل کنید. در مورد ما، مخرج ها قبلاً به صورت محصولات ارائه شده اند و تنها کاری که باید انجام دهیم این است که مخرج کسر اول را گرفته و عوامل گمشده از مخرج کسر دوم را به آن اضافه کنیم. به این ترتیب ما یک مخرج مشترک از فرم به دست می آوریم . در این حالت، کسرهای تفریق شده به ترتیب با استفاده از عوامل اضافی در قالب لگاریتم و عبارت x 2 ·(x+1) به مخرج مشترک آورده می شوند. پس از این، تنها چیزی که باقی می ماند تفریق کسری با مخرج یکسان است که کار سختی نیست.

پس راه حل این است:

ج) معلوم است که حاصل ضرب کسرها، کسری است که صورت آن حاصل ضرب مصدرها و مخرج حاصل ضرب کسرها است، بنابراین.

به راحتی می توان فهمید که می توانید کاهش کسریبا دو و با لگاریتم اعشاری، در نتیجه داریم .

د) از تقسیم کسرها به ضرب حرکت می کنیم و کسر معکوس آن را جایگزین کسری می کنیم. بنابراین

شمارنده کسر حاصل را می توان به صورت نمایش داد ، که از آن ضریب مشترک صورت و مخرج به وضوح قابل مشاهده است - ضریب x، می توانید کسر را با آن کاهش دهید:

پاسخ:

الف)، ب) ، V) ، G) .

لازم به یادآوری است که عملیات با کسرها با در نظر گرفتن ترتیب انجام اقدامات انجام می شود: ابتدا ضرب و تقسیم، سپس جمع و تفریق، و اگر پرانتز وجود داشته باشد، ابتدا اقدامات داخل پرانتز انجام می شود.

مثال.

کارها را با کسر انجام دهید .

راه حل.

ابتدا کسرهای داخل پرانتز را جمع می کنیم و پس از آن ضرب می کنیم:

پاسخ:

در این مرحله، باید سه نکته نسبتاً واضح، اما در عین حال مهم را با صدای بلند بگوییم:

تبدیل عبارات با استفاده از خواص لگاریتم

اغلب، تبدیل عبارات با لگاریتم شامل استفاده از هویت هایی است که تعریف لگاریتم و

دانشگاه دولتی ترانسنیستریا

آنها را T.G. شوچنکو

دانشکده فیزیک و ریاضی

گروه تحلیل ریاضی

و روش های تدریس ریاضی

کار دوره

«تغییر هویت

نمایی و لگاریتمی

اصطلاحات"

کار انجام شده:

دانش آموز گروه _______

دانشکده فیزیک و ریاضی

_________________________

کار رو چک کردم:

_________________________

تیراسپول، 2003

مقدمه……………………………………………………………………………………2

فصل 1. تحولات و روشهای تدریس یکسان در درس جبر مدرسه و آغاز تحلیل……………………………………..4

§1. شکل گیری مهارت در به کارگیری انواع خاصی از تحولات………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

§2. ویژگی های سازماندهی یک سیستم دانش در بررسی تحولات هویتی……………………………………………………………….

§3. برنامه ریاضی………………………………………………….11

فصل 2. تبدیلات و محاسبات یکسان عبارات نمایی و لگاریتمی……………………………...…………………13

§1. تعمیم مفهوم درجه…………………………………..13

§2. تابع نمایی…………………………………………………………………………………………………………………………..

§3. تابع لگاریتمی………………………………….16

فصل 3. تبدیلات یکسان عبارات نمایی و لگاریتمی در عمل..........................................................................19

نتیجه……………………………………………………………………………………………………………………………

فهرست مراجع……………………………………………………………………………………………………………………………………
معرفی

در این کار درسی، تبدیل‌های یکسان توابع نمایی و لگاریتمی در نظر گرفته می‌شود و روش تدریس آنها در درس جبر مدرسه و شروع تجزیه و تحلیل در نظر گرفته می‌شود.

فصل اول این کار روش شناسی آموزش تبدیل هویت در درس ریاضی مدرسه را تشریح می کند و همچنین شامل یک برنامه ریاضی در درس "جبر و آغاز تجزیه و تحلیل" با مطالعه توابع نمایی و لگاریتمی است.

فصل دوم به طور مستقیم به بررسی خود توابع نمایی و لگاریتمی، ویژگی های اساسی آنها در تبدیل هویت می پردازد.

فصل سوم حل مثال‌ها و مسائل با استفاده از تبدیل‌های یکسان توابع نمایی و لگاریتمی است.

مطالعه تغییر شکل‌های مختلف عبارات و فرمول‌ها بخش قابل توجهی از زمان تدریس در درس ریاضی مدرسه را به خود اختصاص می‌دهد. ساده ترین تبدیل ها، بر اساس ویژگی های عملیات حسابی، در حال حاضر در مدرسه ابتدایی و در کلاس های IV-V انجام می شود. اما بار اصلی توسعه مهارت ها و توانایی های انجام تحولات بر عهده درس جبر مدرسه است. این هم به دلیل افزایش شدید تعداد و تنوع دگرگونی های انجام شده و هم به دلیل پیچیدگی فعالیت ها برای توجیه آنها و روشن کردن شرایط کاربرد، به دلیل شناسایی و مطالعه مفاهیم تعمیم یافته هویت، تحول یکسان، تبدیل معادل، نتیجه منطقی.

فرهنگ انجام تبدیل هویت به همان روشی که فرهنگ محاسبات بر اساس دانش کامل از ویژگی های عملیات روی اشیاء (اعداد، بردارها، چند جمله ای ها و غیره) و الگوریتم هایی برای اجرای آنها توسعه می یابد. این خود را نه تنها در توانایی اثبات صحیح تحولات نشان می دهد، بلکه در توانایی یافتن کوتاه ترین مسیر برای انتقال از عبارت تحلیلی اصلی به عبارتی که بیشتر با هدف تبدیل مطابقت دارد، در توانایی نظارت بر تغییرات در حوزه تعریف عبارات تحلیلی در زنجیره ای از تبدیل های یکسان، در سرعت و دقت انجام تبدیل ها.

اطمینان از فرهنگ بالای محاسبات و دگرگونی هویت یک مشکل مهم در آموزش ریاضیات است. با این حال، این مشکل هنوز تا حل رضایت بخش فاصله دارد. گواه این امر، داده های آماری مسئولان آموزش دولتی است که سالانه اشتباهات و روش های غیرمنطقی محاسبات و تبدیل های دانش آموزان طبقات مختلف را هنگام اجرای آزمون ثبت می کنند. این با بازخورد مؤسسات آموزش عالی در مورد کیفیت دانش و مهارت های ریاضی متقاضیان تأیید می شود. نمی توان با نتیجه گیری مقامات آموزش دولتی و دانشگاه ها موافق نبود که سطح ناکافی بالای فرهنگ محاسبات و دگرگونی های یکسان در دوره متوسطه نتیجه رسمی گرایی در دانش دانش آموزان، جدایی نظریه از عمل است.

فصل 1.

تحولات و روش های تدریس یکسان

در درس مدرسه جبر و شروع تحلیل.

§1. شکل گیری مهارت های کاربردی

انواع خاص دگرگونیعناوین.

سیستم تکنیک ها و قوانین برای انجام تبدیل ها، که در مرحله شروع جبر استفاده می شود، کاربردهای بسیار گسترده ای دارد: در مطالعه کل دوره ریاضیات استفاده می شود. با این حال، دقیقاً به دلیل ویژگی پایین آن، این سیستم نیازمند تبدیل‌های اضافی است که ویژگی‌های ساختاری عبارات در حال تبدیل و ویژگی‌های عملیات و توابع تازه معرفی شده را در نظر می‌گیرد. تسلط بر انواع تبدیل های مربوطه با معرفی فرمول های ضرب اختصاری آغاز می شود. سپس تبدیل های مرتبط با عملکرد توان با کلاس های مختلف توابع ابتدایی - نمایی، توان، لگاریتمی، مثلثاتی در نظر گرفته می شود. هر یک از این نوع تحولات یک مرحله یادگیری را طی می کند که در آن توجه بر تسلط بر ویژگی های مشخصه آنها متمرکز است.

با انباشت مواد، می توان ویژگی های مشترک همه تبدیل های مورد بررسی را برجسته کرد و بر این اساس مفاهیم تبدیل های یکسان و معادل را معرفی کرد.

لازم به ذکر است که مفهوم دگرگونی هویت در درس جبر مدرسه نه به طور کلی، بلکه تنها در کاربرد عبارات ارائه شده است. تبدیل ها به دو دسته تقسیم می شوند: تبدیل های یکسان تبدیل عبارات هستند و تبدیل های معادل تبدیل فرمول ها هستند. در مواردی که نیاز به ساده سازی یک بخش از فرمول وجود دارد، یک عبارت در این فرمول برجسته می شود که به عنوان استدلالی برای تبدیل هویت کاربردی عمل می کند. محمول مربوطه بدون تغییر در نظر گرفته می شود.

مربوط به سازماندهی یک سیستم کل نگر از تحولات(سنتز)، سپس هدف اصلی آن تشکیل یک انعطاف پذیر و قدرتمند است. دستگاه مناسب برای حل انواع وظایف آموزشی.

در دوره جبر و آغاز تجزیه و تحلیل، یک سیستم کل نگر از تحولات، که قبلاً در ویژگی های اصلی آن شکل گرفته بود، به تدریج بهبود می یابد. انواع جدیدی از دگرگونی ها نیز به آن اضافه می شوند، اما فقط آن را غنی می کنند، قابلیت های آن را گسترش می دهند، اما ساختار آن را تغییر نمی دهند. روش مطالعه این تبدیل های جدید عملاً با روش مورد استفاده در درس جبر تفاوتی ندارد.

§2. ویژگی های سازمانسیستم های وظیفه

هنگام مطالعه تحولات هویتی

اصل اساسی سازماندهی هر سیستمی از وظایف، ارائه آنها از ساده به پیچیده، با در نظر گرفتن نیاز دانش آموزان برای غلبه بر مشکلات امکان پذیر و ایجاد موقعیت های مشکل ساز است. این اصل اساسی نیاز به مشخصات در رابطه با ویژگی های این ماده آموزشی دارد. برای توصیف سیستم های مختلف وظایف در روش های ریاضی، از این مفهوم استفاده می شود چرخه تمریناتچرخه تمرینات با ترکیب در دنباله ای از تمرینات از جنبه های مختلف مطالعه و تکنیک های ترتیب مطالب مشخص می شود. در رابطه با دگرگونی های هویت، ایده چرخه را می توان به صورت زیر ارائه کرد.

چرخه تمرین ها با مطالعه یک هویت همراه است و هویت های دیگری که در ارتباط طبیعی با آن هستند، پیرامون آن گروه بندی می شوند. این چرخه، همراه با موارد اجرایی، شامل وظایفی است که مستلزم تشخیص قابلیت کاربردی بودن هویت مورد نظر است. هویت مورد مطالعه برای انجام محاسبات در حوزه های عددی مختلف استفاده می شود. ویژگی هویت در نظر گرفته شده است. به ویژه، شکل های گفتاری مرتبط با آن سازماندهی می شوند.

وظایف در هر چرخه به دو گروه تقسیم می شود. اولی شامل وظایفی است که در طی آشنایی اولیه با هویت انجام می شود. آنها به عنوان مواد آموزشی برای چندین درس متوالی که توسط یک موضوع متحد می شوند، خدمت می کنند. گروه دوم تمرین ها هویت مورد مطالعه را با کاربردهای مختلف مرتبط می کند. این گروه یک وحدت ترکیبی را تشکیل نمی دهد - تمرینات در اینجا در موضوعات مختلف پراکنده است.

ساختار چرخه توصیف شده به مرحله توسعه مهارت ها در به کارگیری انواع خاصی از تحولات اشاره دارد. در مرحله نهایی - مرحله سنتز، چرخه ها اصلاح می شوند. اولاً، هر دو گروه از کارها با هم ترکیب می شوند تا یک چرخه "گسترش یافته" را تشکیل دهند و ساده ترین آنها از نظر عبارت یا پیچیدگی تکمیل کار از گروه اول حذف می شوند. انواع باقی مانده وظایف پیچیده تر می شوند. ثانیاً، ادغام چرخه‌های مربوط به هویت‌های مختلف وجود دارد که به دلیل آن نقش اقدامات برای تشخیص کاربردی بودن یک هویت خاص افزایش می‌یابد.

اجازه دهید ویژگی‌های چرخه‌های وظیفه مربوط به هویت‌ها را برای توابع ابتدایی یادداشت کنیم. این ویژگی ها به این دلیل است که اولاً هویت های متناظر در ارتباط با مطالعه مواد کاربردی مورد مطالعه قرار می گیرند و ثانیاً دیرتر از هویت های گروه اول ظاهر می شوند و با استفاده از مهارت های از قبل شکل گرفته برای انجام دگرگونی های هویت مورد مطالعه قرار می گیرند. .

هر تابع ابتدایی تازه معرفی شده به طور چشمگیری دامنه اعدادی را که می توان به صورت جداگانه تعیین و نامگذاری کرد، گسترش می دهد. بنابراین، اولین گروه از وظایف چرخه باید شامل وظایفی برای ایجاد ارتباط بین این حوزه های عددی جدید و حوزه اصلی اعداد گویا باشد. بیایید نمونه هایی از چنین وظایفی را بیان کنیم.

مثال 1 . محاسبه:

در کنار هر عبارت یک هویت نشان داده شده است، در چرخه هایی که وظایف پیشنهادی ممکن است وجود داشته باشد. هدف از چنین وظایفی تسلط بر ویژگی های رکوردها، از جمله نمادهای عملیات و توابع جدید، و توسعه مهارت های گفتاری ریاضی است.

بخش قابل توجهی از استفاده از تبدیل هویت مرتبط با توابع ابتدایی بر روی حل معادلات غیرمنطقی و ماورایی است. چرخه های مربوط به همسان سازی هویت ها فقط ساده ترین معادلات را شامل می شود، اما در اینجا توصیه می شود کار بر روی روش حل چنین معادلاتی انجام شود: کاهش آن با جایگزینی مجهول با یک معادله جبری.

ترتیب مراحل این راه حل به شرح زیر است:

الف) تابعی را پیدا کنید که این معادله را می توان به شکل آن نشان داد.

ب) جایگزینی را انجام دهید و معادله را حل کنید.

ج) هر یک از معادلات را حل کنید، مجموعه ریشه های معادله کجاست.

هنگام استفاده از روش توصیف شده، مرحله b) اغلب به طور ضمنی، بدون معرفی نمادی برای . علاوه بر این، دانش‌آموزان اغلب ترجیح می‌دهند، از مسیرهای مختلف منتهی به یافتن پاسخ، مسیری را انتخاب کنند که سریع‌تر و آسان‌تر به معادله جبری منتهی شود.

مثال 2 . معادله را حل کنید.

راه اول:

راه دوم:

در اینجا می بینید که با روش اول مرحله a) دشوارتر از روش دوم است. روش اول "شروع کردن با آن دشوارتر است"، اگرچه مسیر بعدی راه حل بسیار ساده تر است. از سوی دیگر، روش دوم دارای مزایای سهولت بیشتر و دقت بیشتر در یادگیری کاهش به معادله جبری است.

برای یک دوره جبر مدرسه، وظایف معمولی هستند که در آن انتقال به یک معادله جبری حتی ساده تر از این مثال است. بار اصلی چنین وظایفی مربوط به شناسایی مرحله c) به عنوان بخشی مستقل از فرآیند حل مرتبط با استفاده از ویژگی های تابع ابتدایی مورد مطالعه است.

مثال 3 . معادله را حل کنید:

این معادلات به معادلات کاهش می یابد: a) یا ; ب) یا . برای حل این معادلات، آگاهی از ساده ترین حقایق در مورد تابع نمایی مورد نیاز است: یکنواختی آن، محدوده مقادیر. مانند مثال قبلی، معادلات a) و b) را می توان به عنوان اولین گروه از یک سری تمرینات برای حل معادلات نمایی درجه دوم طبقه بندی کرد.

بنابراین، به طبقه‌بندی وظایف در چرخه‌های مربوط به حل معادلات ماورایی می‌رسیم که شامل یک تابع نمایی است:

1) معادلاتی که به معادلات شکل تقلیل می یابند و پاسخ ساده و کلی دارند: ;

2) معادلاتی که به معادلات تقلیل می‌یابند، جایی که یک عدد صحیح است، یا، جایی که ;

3) معادلاتی که به معادلات تقلیل می یابند و نیازمند تحلیل صریح شکلی هستند که عدد در آن نوشته شده است .

وظایف برای سایر توابع ابتدایی را می توان به طور مشابه طبقه بندی کرد.

بخش قابل توجهی از هویت های مورد مطالعه در جبر و جبر و اصول دروس تجزیه و تحلیل در آنها اثبات یا حداقل تبیین شده است. این جنبه از بررسی هویت ها برای هر دو دوره از اهمیت بالایی برخوردار است، زیرا استدلال اثباتی در آنها دقیقاً در رابطه با هویت ها با بیشترین وضوح و دقت انجام می شود. فراتر از این مطالب، شواهد معمولاً کمتر کامل هستند؛ همیشه از شواهد مورد استفاده متمایز نمی شوند.

از ویژگی‌های عملیات حسابی به عنوان پشتیبان برای اثبات هویت استفاده می‌شود.

تأثیر آموزشی محاسبات و دگرگونی های یکسان می تواند در توسعه تفکر منطقی باشد، اگر فقط دانش آموزان به طور سیستماتیک ملزم به توجیه محاسبات و دگرگونی های یکسان باشند، و در توسعه تفکر عملکردی، که به طرق مختلف به دست می آید. اهمیت محاسبات و دگرگونی های یکسان در رشد اراده، حافظه، هوش، خویشتن داری و ابتکار خلاق کاملاً آشکار است.

الزامات محاسبات روزمره و صنعتی دانش آموزان را ملزم به توسعه مهارت های قوی و خودکار در محاسبات منطقی و تغییر هویت می کند. این مهارت‌ها در فرآیند هر کار محاسباتی ایجاد می‌شوند، با این حال، تمرین‌های آموزشی ویژه در محاسبات و تبدیل‌های سریع ضروری است.

بنابراین، اگر درس شامل حل معادلات لگاریتمی با استفاده از هویت لگاریتمی پایه باشد، مفید است که در طرح درس تمرین‌های شفاهی ساده‌سازی یا محاسبه معانی عبارات را گنجانده شود: , , . هدف از تمرینات همیشه به دانش آموزان ابلاغ می شود. در طول تمرین، ممکن است لازم باشد از دانش‌آموزان بخواهیم که تغییرات فردی، اقدامات یا راه‌حل یک مشکل را توجیه کنند، حتی اگر این برنامه‌ریزی نشده باشد. در جاهایی که راه‌های مختلفی برای حل یک مشکل امکان‌پذیر است، توصیه می‌شود همیشه سوالاتی بپرسید: "مشکل چگونه حل شد؟"، "چه کسی مشکل را به روش دیگری حل کرد؟"

مفاهیم هویت و تبدیل هویت به صراحت در درس جبر کلاس ششم معرفی شده است. خود تعریف عبارات یکسان را نمی توان عملاً برای اثبات هویت دو عبارت استفاده کرد و درک کرد که ماهیت تبدیل های یکسان این است که تعاریف و ویژگی های آن اعمالی را که در عبارت نشان داده شده اند به عبارت اعمال کنند یا به آن اضافه کنند. عبارتی است که به طور یکسان برابر با 0 است، یا در ضرب آن در عبارتی یکسان برابر با یک است. اما حتی با تسلط بر این مفاد، دانش‌آموزان اغلب نمی‌فهمند که چرا این تغییر شکل‌ها به ما اجازه می‌دهد تا اظهار کنیم که عبارات اصلی و حاصل یکسان هستند، یعنی. برای هر سیستم (مجموعه) مقادیر متغیر همان مقادیر را بگیرید.

همچنین مهم است که اطمینان حاصل شود که دانش آموزان به وضوح درک می کنند که چنین نتیجه گیری هایی از تبدیل های یکسان پیامدهای تعاریف و ویژگی های اقدامات مربوطه است.

دستگاه دگرگونی‌های هویتی که در سال‌های گذشته انباشته شده است، در کلاس ششم گسترش یافته است. این بسط با معرفی هویتی آغاز می‌شود که ویژگی حاصلضرب قدرت‌ها را با پایه‌های یکسان بیان می‌کند: , جایی که , اعداد صحیح هستند.

§3. برنامه ریاضی.

در درس مدرسه "جبر و آغاز تحلیل" دانش آموزان به طور سیستماتیک توابع نمایی و لگاریتمی و خواص آنها، تبدیل های یکسان عبارات لگاریتمی و نمایی و کاربرد آنها در حل معادلات و نامساوی مربوطه را مطالعه می کنند و با مفاهیم و گزاره های اساسی آشنا می شوند. .

در کلاس یازدهم، درس جبر 3 ساعت در هفته و در مجموع 102 ساعت در سال طول می کشد. این برنامه 36 ساعت طول می کشد تا توابع نمایی، لگاریتمی و توان را مطالعه کند.

این برنامه شامل بررسی و مطالعه مسائل زیر است:

مفهوم درجه با توان منطقی. حل معادلات غیر منطقی تابع نمایی، خواص و نمودار آن. تبدیلات یکسان عبارات نمایی. حل معادلات نمایی و نامساوی. لگاریتم یک عدد. ویژگی های اصلی لگاریتم ها تابع لگاریتمی، خواص و نمودار آن. حل معادلات لگاریتمی و نامساوی. مشتق تابع نمایی. عدد و لگاریتم طبیعی مشتق تابع توان.

هدف اصلی بخش تابع نمایی و لگاریتمی آشنایی دانش آموزان با توابع نمایی، لگاریتمی و توان است. حل معادلات و نابرابری های نمایی و لگاریتمی را به دانش آموزان آموزش دهید.

مفاهیم ریشه هفتم و درجه با توان گویا تعمیم مفاهیم ریشه دوم و درجه با توان صحیح است. دانش‌آموزان باید به این نکته توجه داشته باشند که ویژگی‌های ریشه‌ها و توان‌ها با توان‌های گویا در اینجا مشابه ویژگی‌هایی است که ریشه‌های مربعی قبلاً مطالعه شده و توان‌هایی با توان‌های صحیح دارند. لازم است زمان کافی برای تمرین ویژگی های درجه ها و توسعه مهارت های دگرگونی هویت اختصاص داده شود. مفهوم درجه با توان غیرمنطقی بر مبنای بصری و شهودی معرفی شده است. این ماده نقش کمکی ایفا می کند و هنگام معرفی تابع نمایی استفاده می شود.

مطالعه خواص توابع نمایی، لگاریتمی و توانی مطابق با طرح کلی پذیرفته شده برای مطالعه توابع ساخته شده است. در این مورد، یک نمای کلی از ویژگی ها بسته به مقادیر پارامتر ارائه می شود. نابرابری های نمایی و لگاریتمی بر اساس ویژگی های مورد مطالعه توابع حل می شوند.

یکی از ویژگی های دوره، سیستم سازی و تعمیم دانش دانش آموزان، تثبیت و توسعه مهارت های به دست آمده در دوره جبر است که هم هنگام مطالعه مطالب جدید و هم در طول تکرار کلی انجام می شود.
فصل 2.

تبدیل هویت و محاسبات

عبارات نمایی و لگاریتمی

§1. تعمیم مفهوم درجه.

تعریف:ریشه ام یک عدد خالص عددی است که توان آن برابر است با .

بر اساس این تعریف، ریشه ام یک عدد، جواب معادله است. تعداد ریشه های این معادله به و بستگی دارد. بیایید عملکرد را در نظر بگیریم. همانطور که مشخص است، در بازه این تابع برای هر مقدار افزایش می یابد و همه مقادیر را از بازه می گیرد. با توجه به قضیه ریشه، معادله هر یک ریشه غیر منفی و علاوه بر این، فقط یک دارد. او نامیده می شود ریشه حسابی درجه یک عددو نشان دهید؛ شماره تماس گرفته می شود شاخص ریشه، و خود شماره است بیان رادیکال. این علامت رادیکال نیز نامیده می شود.

تعریف: ریشه حسابی توان دهم یک عدد عددی غیر منفی است که توان آن برابر است با .

برای اعداد زوج تابع زوج است. نتیجه این است که اگر , پس معادله علاوه بر ریشه یک ریشه نیز دارد. اگر، پس یک ریشه وجود دارد: ; اگر، پس این معادله ریشه ندارد، زیرا توان زوج هر عددی غیر منفی است.

برای مقادیر فرد، تابع در طول کل خط اعداد افزایش می یابد. محدوده آن مجموعه ای از تمام اعداد واقعی است. با اعمال قضیه ریشه، در می یابیم که معادله یک ریشه برای هر و، به ویژه، برای . این ریشه برای هر مقدار با نشان داده می شود.

برای ریشه های درجه فرد، برابری درست است. در واقع، یعنی عدد ریشه ام است. اما چنین ریشه ای برای عجیب و غریب تنها یک است. از این رو، .

یادداشت 1:برای هر واقعی

اجازه دهید خواص شناخته شده ریشه های حسابی درجه هفتم را به یاد بیاوریم.

برای هر عدد طبیعی، عدد صحیح و هر عدد صحیح غیرمنفی و برابری ها معتبر است:

مدرک با توان منطقی.

عبارت برای همه و به جز مورد تعریف شده است. بیایید ویژگی های چنین قدرت هایی را به یاد بیاوریم.

برای هر عدد و هر عدد صحیح و برابری ها معتبر هستند:

ما همچنین توجه داشته باشید که اگر، سپس در و در.

تعریف:به توان یک عدد با توان گویا که یک عدد صحیح و یک عدد طبیعی است، عدد می گویند.

بنابراین، طبق تعریف.

با تعریف فرمول‌بندی شده درجه با توان گویا، ویژگی‌های پایه درجه‌ها حفظ می‌شوند که برای هر توانمندی صادق است (تفاوت این است که خواص فقط برای پایه‌های مثبت صادق است).

§2. تابع نمایی.

تعریف:تابع داده شده با فرمول (where ) فراخوانی می شود تابع نمایی با پایه .

اجازه دهید ویژگی های اصلی تابع نمایی را فرموله کنیم.

نمودار تابع (شکل 1)

این فرمول ها نامیده می شوند ویژگی های اساسی درجه ها

همچنین می توانید متوجه شوید که تابع در مجموعه اعداد واقعی پیوسته است.

§3. تابع لگاریتمی

تعریف: لگاریتم اعداد به پایه را توانی می گویند که پایه باید به آن افزایش یابد. برای دریافت شماره

فرمول (where , and ) نامیده می شود هویت لگاریتمی پایه.

هنگام کار با لگاریتم، از ویژگی های زیر استفاده می شود که از ویژگی های تابع نمایی حاصل می شود:

برای هرچی( )و هرگونه مثبت و برابری برآورده می شود:

5. برای هر واقعی .

خواص اصلی لگاریتم ها به طور گسترده ای در هنگام تبدیل عبارات حاوی لگاریتم استفاده می شود. به عنوان مثال، فرمول حرکت از یک پایه لگاریتمی به پایه دیگر اغلب استفاده می شود: .

فرض کنید یک عدد مثبت برابر با 1 نباشد.

تعریف:تابع داده شده توسط فرمول نامیده می شود تابع لگاریتمی با پایه

اجازه دهید ویژگی های اصلی تابع لگاریتمی را فهرست کنیم.

1. دامنه تعریف یک تابع لگاریتمی مجموعه ای از تمام اعداد مثبت است، یعنی. .

2. محدوده مقادیر یک تابع لگاریتمی مجموعه ای از تمام اعداد واقعی است.

3. تابع لگاریتمی در کل دامنه تعریف افزایش می یابد (در) یا کاهش می یابد (در).

نمودار تابع (شکل 2)

نمودارهای توابع نمایی و لگاریتمی که پایه یکسانی دارند نسبت به یک خط مستقیم متقارن هستند.(شکل 3).

فصل 3.

تبدیلات یکسان نمایی و

عبارات لگاریتمی در عمل

تمرین 1.

محاسبه:

راه حل:

پاسخ:; ; ; ; . ، ما آن را دریافت می کنیم

هنگام مطالعه این مطالب روش هایی را برای پرورش مهارت در دانش آموزان در نظر گرفتم. وی همچنین برنامه ای در ریاضیات برای مطالعه درس توابع نمایی و لگاریتمی در درس «جبر و آغاز تحلیل» ارائه کرد.

این کار وظایفی با پیچیدگی و محتوای متفاوت با استفاده از دگرگونی‌های یکسان ارائه کرد. از این وظایف می توان برای انجام آزمون ها یا کار مستقل برای آزمایش دانش دانش آموزان استفاده کرد.

کار دوره، به نظر من، در چارچوب روش شناسی تدریس ریاضیات در موسسات آموزشی متوسطه انجام شد و می تواند به عنوان یک کمک بصری برای معلمان مدرسه و همچنین برای دانش آموزان تمام وقت و پاره وقت استفاده شود.

فهرست ادبیات مورد استفاده:

1. جبر و آغاز تحلیل. اد. کولموگورووا A.N. م.: آموزش و پرورش، 1991.
2. برنامه برای مدارس متوسطه، سالن های ورزشی، لیسیوم ها. ریاضی 5-11 پایه. M.: Bustard، 2002.
3. I.F. شاریگین، V.I. گلوبف درس اختیاری ریاضی (حل مسئله). اوخ کمک هزینه کلاس یازدهم م.: آموزش و پرورش، 1991.
4. V.A. اوگانسیان و همکاران روش های تدریس ریاضی در دوره متوسطه: روش های عمومی; کتاب درسی برای دانشجویان دانشکده فیزیک و ریاضی موسسات آموزشی. -ویرایش دوم بازنگری و گسترش یافت.م.: آموزش، 1980.
5. چرکاسف R.S.، Stolyar A.A. روش های تدریس ریاضی در دوره متوسطه. م.: آموزش و پرورش، 1985.
6. مجله "ریاضیات در مدرسه".

اگورووا ویکتوریا والریونا

معلم ریاضی

بالاترین رده صلاحیت

موضوع: «تحول هویت

عبارات لگاریتمی"

دانش و مهارت هایی که دانش آموزان پس از مطالعه این درس باید به آنها مسلط شوند:

تعریف لگاریتم یک عدد، هویت لگاریتمی اساسی، خواص لگاریتم را بدانید.

قادر به انجام تبدیل عبارات حاوی لگاریتم و محاسبه لگاریتم باشد.

ادبیات:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. جبر و آغاز تحلیل: کتاب درسی برای پایه های 10-11 در موسسات آموزش عمومی. - م.: آموزش و پرورش، 2001.

2. Kochagin V.V.، Kochagina M.V.، دوره آمادگی فشرده برای آزمون دولتی واحد. - M.: Eksmo، 2009.

3. Merzlyak A.G.، Polonsky V.B.، Yakir M.S.، شبیه ساز جبری: کتابچه راهنمای دانش آموزان و متقاضیان. - M.: Ilexa، 2005.

4. گوسف V.A.، Mordkovich A.G. ریاضیات: مواد مرجع: کتاب برای دانش آموزان. - م.: آموزش و پرورش، 2001.

طرح درس:

در طول کلاس ها:

1) لگاریتم یک کلمه یونانی است که از 2 کلمه تشکیل شده است: "logos" - نسبت، "arithmos" - عدد. این بدان معناست که لگاریتم عددی است که نسبت را اندازه می گیرد. نشریه ای در سال 1614 گزارش داد که ناپیر لگاریتم ها را اختراع کرد. بعداً جداول لگاریتمی را تهیه کرد که امروزه به عنوان جداول برادیس برای ما شناخته می شوند. در کمتر از یک قرن، جداول در سراسر جهان گسترش یافته و به یک ابزار محاسباتی ضروری تبدیل شده اند. پس از آن، آنها، همانطور که بود، در یک دستگاه مناسب ساخته شدند که روند محاسبه را بسیار سرعت می بخشد - یک قانون اسلاید، که تا دهه هفتاد قرن بیستم استفاده می شد.

پیوست 1.

2) لگاریتم عدد مثبتببر اساس آ، و و بزرگتر از صفر است و مساوی یک نیست،توانی است که یک عدد باید به آن افزایش یابدآ برای دریافت شمارهب

این برابری، بیانگر تعریف لگاریتم، نامیده می شودهویت لگاریتمی پایه .

سی

یا 1

پ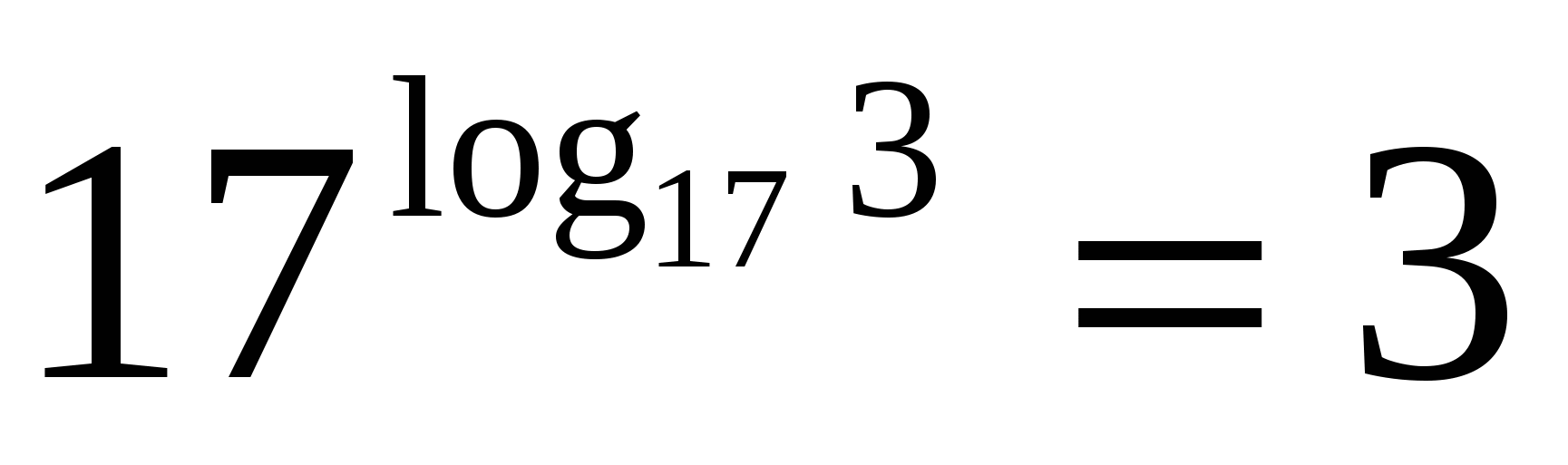

پایه توان و پایه لگاریتم هفده است، یعنی با توجه به هویت لگاریتمی پایه، مقدار عبارت سه است.

بیایید به صورت شفاهی کار کنیم:

SCH
FIR-BELLE

در باره پایین دوم برابر با صفر نقطه پنج است، یعنی عبارت برابر است با جذر حسابی پنج.

پ

ضمیمه 2.

برابری یعنی که

از تعریف لگاریتم برابری های مهم زیر به دست می آید:

مثلا:

پ
پیوست 3.

بیایید به وظایف آزمون یکپارچه دولتی برویم:

ضمیمه 4.

3
) نماد و نام خاصی برای لگاریتم پایه ده وجود داردلگاریتم اعشاری .

L
تقویم پایهه تماس گرفتلگاریتم طبیعی .

ن
مثلا،

4) خواص زیر از تعریف لگاریتم به دست می آید. تمام خصوصیات فقط برای مقادیر مثبت متغیرهای موجود در زیر علائم لگاریتم فرموله و اثبات می شوند.

لگاریتم حاصل ضرب دو عدد مثبت به قاعده آبرابر با مجموع لگاریتم این اعداد با پایه یکسان است.

TsOR 2

مثلا،

ز
تکلیف 1.

وظیفه 2.بیان را ساده کنید

که در
بیایید از راه حل مثال قبل استفاده کنیم. جایگزین خواهیم کرد

لطفاً توجه داشته باشید که لگاریتم مربع است، بنابراین مجموع باید مجذور شود. با استفاده از فرمول مربع مجموع، پرانتزها را باز می کنیم. اجازه دهید اصطلاحات مشابهی را ارائه کنیم.

5) لگاریتم ضریب برابر است با اختلاف لگاریتم تقسیم کننده و مقسوم علیه.

سی

به پایه توان و پایه لگاریتم توجه کنید - آنها یکسان هستند.

یا 3

آر

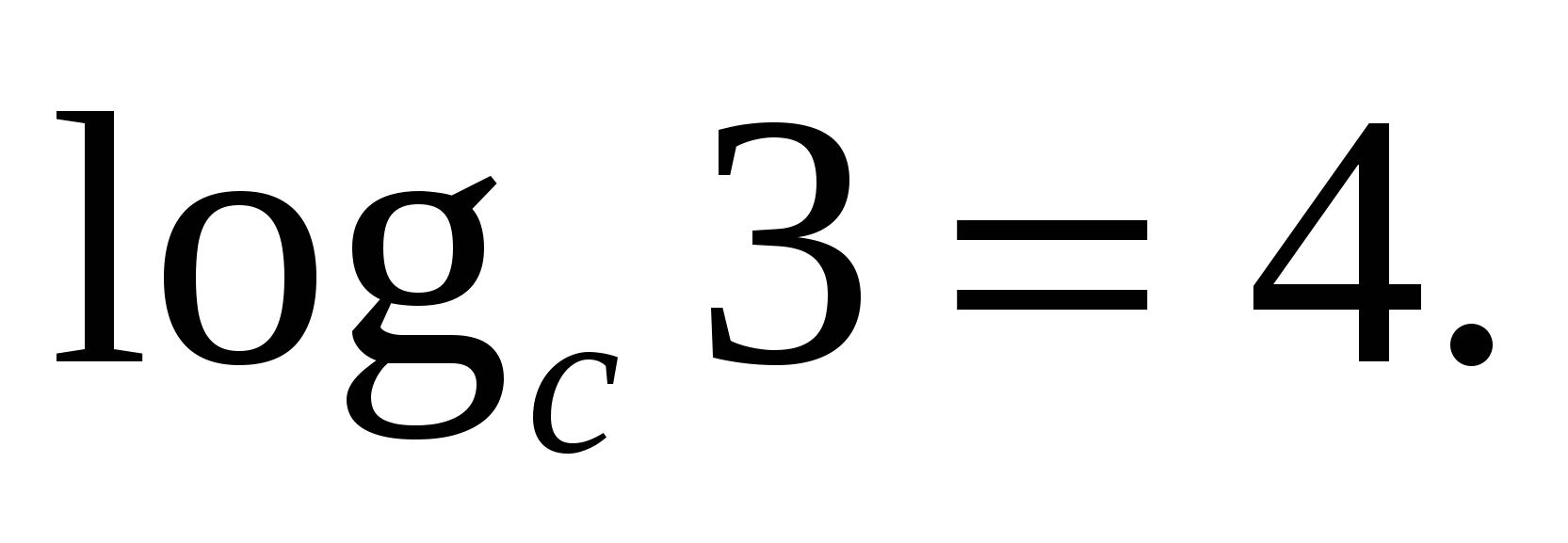بیایید با استفاده از یک مثال به کاربرد این فرمول نگاه کنیم:

ز
تکلیف 1.مقدار عبارت if را پیدا کنید

وظیفه 2.مقدار را پیدا کنید بتوسط لگاریتم آن

6) لگاریتم یک توان به پایهآ ، برابر است با حاصل ضرب توان و لگاریتم با استفاده از یک پایه.

TsOR 4

مثلا،

ز
تکلیف 1.محاسبه کنید اگر

بیایید بیان را ساده کنیم

فرمول

تماس گرفت فرمول انتقال به یک پایه جدید

ز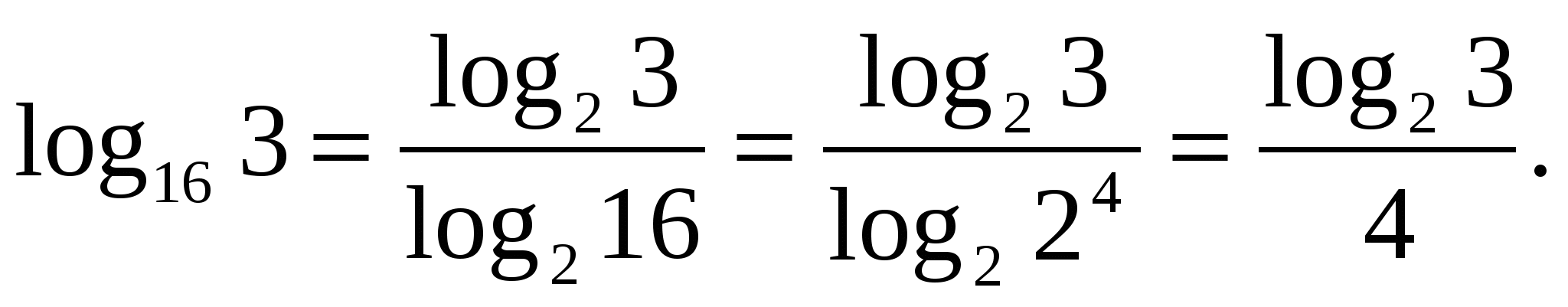

تکلیف 1.با استفاده از لگاریتم پایه 2 بیان کنید.

وظیفه 2.محاسبه

TsOR 5

TsOR 6

مثلا،

ز

تکلیف 1.محاسبه

ز
وظیفه 2.محاسبه

9) تبدیلات لگاریتمی را می توان تنها در مواردی شروع کرد کهاگر تمام خصوصیات لگاریتم را به خاطر داشته باشید. پس از تکرار آنها، وظایفی را برای تبدیل عبارات لگاریتمی از طرف دیگر در نظر خواهیم گرفت.

برای تبدیل مجموع یا تفاضل عبارات لگاریتمی، گاهی اوقات کافی است از تعریف لگاریتم و اغلب از خواص لگاریتم یک محصول یا ضریب استفاده کنیم.

ز
تکلیف 1.محاسبه

بیایید آن را به دو روش حل کنیم.

1 راه، با استفاده از تعریف لگاریتم:

روش 2، بر اساسخاصیت لگاریتم یک ضریب:

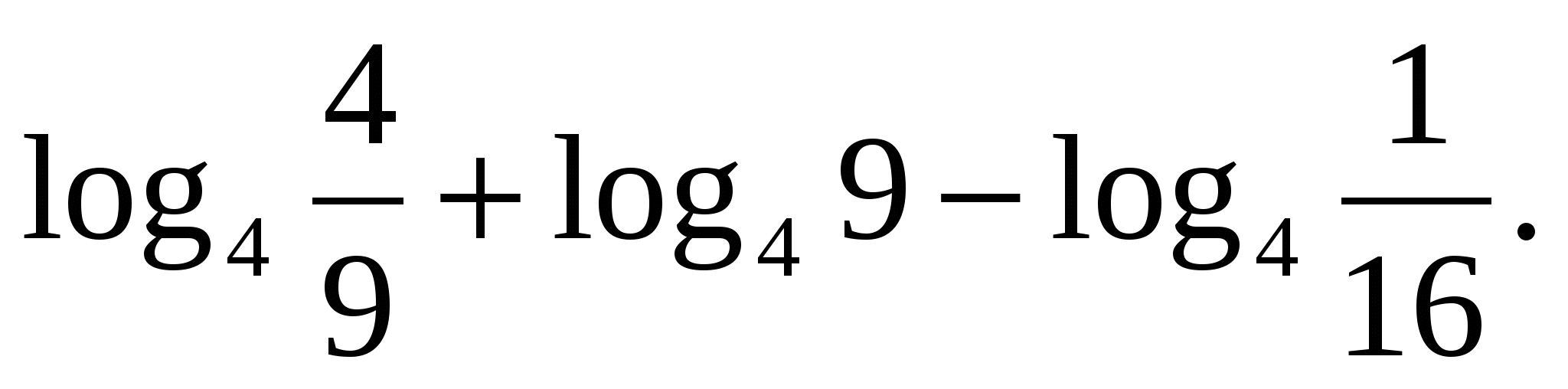
وظیفه 2.معنی عبارت را پیدا کنید

بیایید ابتدا فرمول را اعمال کنیملگاریتم محصول، سپس تعریف لگاریتم.

هویت لگاریتمی اصلی هنگام تبدیل عبارات حاوی لگاریتم به عنوان یک توان استفاده می شود. ایده چنین عملیاتی به دست آوردن پایه های مساوی از توان ها و پایه های لگاریتم است.

گاهی اوقات لازم است که بیان را تغییر دهیمبا خواص لگاریتم و با خواص درجه نیز با استفاده از فرمول انتقال به راحتی می توانید از یک پایه به پایه دیگر حرکت کنید. در موارد دیگر، چندین ویژگی باید اعمال شود.

ز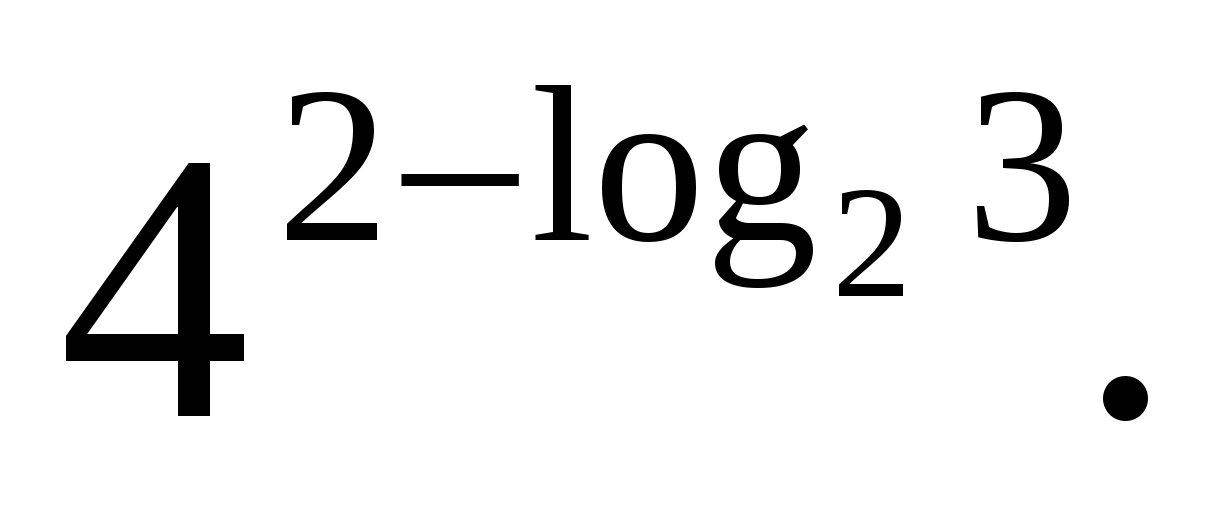
تکلیف 3.محاسبه

ز
تکلیف 4.معنی عبارت را پیدا کنید

وظیفه 5.معنی عبارت را پیدا کنید

ز
تکلیف 6.آن را به صورت اختلاف لگاریتم بیان کنید

ن
بزرگترین مشکل در تبدیل عبارات لگاریتمی تحت رادیکال است. در فرآیند تبدیل ها، باید مدول های عبارات لگاریتمی را در نظر گرفت که برای حل آن ها باید اعداد غیر منطقی یا یک عدد گویا و یک عدد غیر منطقی را با هم مقایسه کرد. ما به طور مداوم عمل خواهیم کرد. بیایید به بیان زیر رادیکال درونی نگاه کنیم.

بیایید آن را با عبارت اصلی جایگزین کنیم.

لازم به ذکر است که تبدیل عبارات لگاریتمی در حل معادلات و نابرابری ها یا مطالعه توابع نیز قابل مشاهده است، بنابراین می توانند به صورت ضمنی در وظایف گروه B و C حضور داشته باشند.

10) جمع بندی سوالات:

لگاریتم به پایه 10 نامیده می شود

لگاریتم پایه

لگاریتم اصلی

لگاریتم طبیعی

لگاریتم اعشاری

2) چه ارزش هایی می تواند داشته باشد؟ایکس در بیان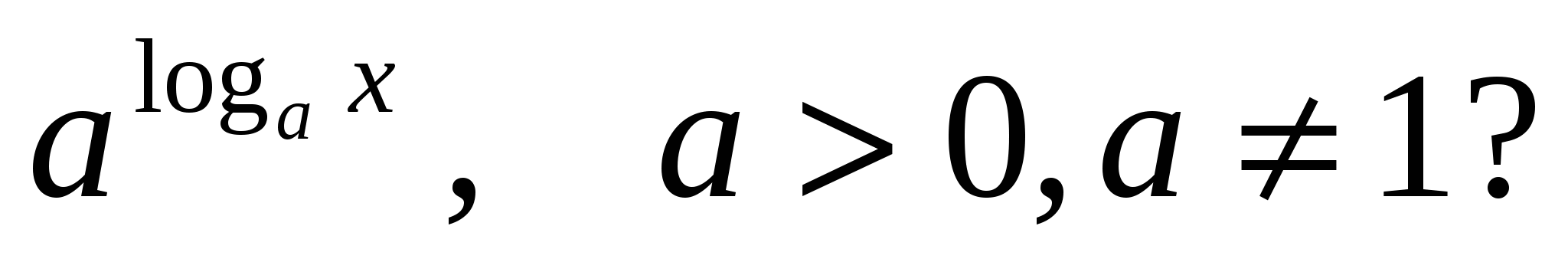

مقدار تعریف نشده است

5) نسبتی بدهید که برای همه صادق استایکس ≠ 0 .

6) نسبت صحیح فرمول انتقال به پایه جدید را مشخص کنید.

7) برابری صحیح را مشخص کنید

11) تست کنترل

مثال 1 . محاسبه:

در کنار هر عبارت یک هویت نشان داده شده است، در چرخه هایی که وظایف پیشنهادی ممکن است وجود داشته باشد. هدف از چنین وظایفی تسلط بر ویژگی های رکوردها، از جمله نمادهای عملیات و توابع جدید، و توسعه مهارت های گفتاری ریاضی است.

بخش قابل توجهی از استفاده از تبدیل هویت مرتبط با توابع ابتدایی بر روی حل معادلات غیرمنطقی و ماورایی است. چرخه های مربوط به همسان سازی هویت ها فقط ساده ترین معادلات را شامل می شود، اما در اینجا توصیه می شود کار بر روی روش حل چنین معادلاتی انجام شود: کاهش آن با جایگزینی مجهول با یک معادله جبری.

ترتیب مراحل این راه حل به شرح زیر است:

الف) تابع را پیدا کنید

، که این معادله را می توان به صورت ;

ب) جایگزینی انجام دهید

و معادله را حل کنید؛

ج) هر یک از معادلات را حل کنید

، مجموعه ریشه های معادله کجاست.

هنگام استفاده از روش توصیف شده، مرحله b) اغلب به طور ضمنی، بدون معرفی یک نماد برای انجام می شود

. علاوه بر این، دانش‌آموزان اغلب ترجیح می‌دهند، از مسیرهای مختلف منتهی به یافتن پاسخ، مسیری را انتخاب کنند که سریع‌تر و آسان‌تر به معادله جبری منتهی شود.

مثال 2 . معادله را حل کنید

.

راه اول:

راه دوم:

در اینجا می بینید که با روش اول مرحله a) دشوارتر از روش دوم است. روش اول "شروع کردن با آن دشوارتر است"، اگرچه مسیر بعدی راه حل بسیار ساده تر است. از سوی دیگر، روش دوم دارای مزایای سهولت بیشتر و دقت بیشتر در یادگیری کاهش به معادله جبری است.

برای یک دوره جبر مدرسه، وظایف معمولی هستند که در آن انتقال به یک معادله جبری حتی ساده تر از این مثال است. بار اصلی چنین وظایفی مربوط به شناسایی مرحله c) به عنوان بخشی مستقل از فرآیند حل مرتبط با استفاده از ویژگی های تابع ابتدایی مورد مطالعه است.

مثال 3 . معادله را حل کنید:

; ب) .

این معادلات به معادلات کاهش می یابد: الف)

یا ؛ ب) یا . برای حل این معادلات، آگاهی از ساده ترین حقایق در مورد تابع نمایی مورد نیاز است: یکنواختی آن، محدوده مقادیر. مانند مثال قبلی، معادلات a) و b) را می توان به عنوان اولین گروه از یک سری تمرینات برای حل معادلات نمایی درجه دوم طبقه بندی کرد.

بنابراین، به طبقه‌بندی وظایف در چرخه‌های مربوط به حل معادلات ماورایی می‌رسیم که شامل یک تابع نمایی است:

1) معادلاتی که به معادلات شکل کاهش می یابد

و داشتن یک پاسخ ساده و کلی: ;

2) معادلاتی که به معادلات کاهش می یابند

، کجا یک عدد صحیح است، یا، کجا ;

3) معادلاتی که به معادلات کاهش می یابند

و نیاز به تحلیل صریح شکلی که عدد در آن نوشته شده است .

وظایف برای سایر توابع ابتدایی را می توان به طور مشابه طبقه بندی کرد.

بخش قابل توجهی از هویت های مورد مطالعه در جبر و جبر و اصول دروس تجزیه و تحلیل در آنها اثبات یا حداقل تبیین شده است. این جنبه از بررسی هویت ها برای هر دو دوره از اهمیت بالایی برخوردار است، زیرا استدلال اثباتی در آنها دقیقاً در رابطه با هویت ها با بیشترین وضوح و دقت انجام می شود. فراتر از این مطالب، شواهد معمولاً کمتر کامل هستند؛ همیشه از شواهد مورد استفاده متمایز نمی شوند.

از ویژگی‌های عملیات حسابی به عنوان پشتیبان برای اثبات هویت استفاده می‌شود.

تأثیر آموزشی محاسبات و دگرگونی های یکسان می تواند در توسعه تفکر منطقی باشد، اگر فقط دانش آموزان به طور سیستماتیک ملزم به توجیه محاسبات و دگرگونی های یکسان باشند، و در توسعه تفکر عملکردی، که به طرق مختلف به دست می آید. اهمیت محاسبات و دگرگونی های یکسان در رشد اراده، حافظه، هوش، خویشتن داری و ابتکار خلاق کاملاً آشکار است.

الزامات محاسبات روزمره و صنعتی دانش آموزان را ملزم به توسعه مهارت های قوی و خودکار در محاسبات منطقی و تغییر هویت می کند. این مهارت‌ها در فرآیند هر کار محاسباتی ایجاد می‌شوند، با این حال، تمرین‌های آموزشی ویژه در محاسبات و تبدیل‌های سریع ضروری است.

بنابراین، اگر درس شامل حل معادلات لگاریتمی با استفاده از هویت لگاریتمی پایه باشد.

، پس از آن مفید است که در طرح درس تمرین های شفاهی در مورد ساده سازی یا محاسبه معانی عبارات گنجانده شود: ، ، . هدف از تمرینات همیشه به دانش آموزان ابلاغ می شود. در طول تمرین، ممکن است لازم باشد از دانش‌آموزان بخواهیم که تغییرات فردی، اقدامات یا راه‌حل یک مشکل را توجیه کنند، حتی اگر این برنامه‌ریزی نشده باشد. در جاهایی که راه‌های مختلفی برای حل یک مشکل امکان‌پذیر است، توصیه می‌شود همیشه سوالاتی بپرسید: "مشکل چگونه حل شد؟"، "چه کسی مشکل را به روش دیگری حل کرد؟"

مفاهیم هویت و تبدیل هویت به صراحت در درس جبر کلاس ششم معرفی شده است. خود تعریف عبارات یکسان را نمی توان عملاً برای اثبات هویت دو عبارت استفاده کرد و درک کرد که ماهیت تبدیل های یکسان این است که تعاریف و ویژگی های آن اعمالی را که در عبارت نشان داده شده اند به عبارت اعمال کنند یا به آن اضافه کنند. عبارتی است که به طور یکسان برابر با 0 است، یا در ضرب آن در عبارتی یکسان برابر با یک است. اما حتی با تسلط بر این مفاد، دانش‌آموزان اغلب نمی‌فهمند که چرا این تغییر شکل‌ها به ما اجازه می‌دهد تا اظهار کنیم که عبارات اصلی و حاصل یکسان هستند، یعنی. برای هر سیستم (مجموعه) مقادیر متغیر همان مقادیر را بگیرید.

همچنین مهم است که اطمینان حاصل شود که دانش آموزان به وضوح درک می کنند که چنین نتیجه گیری هایی از تبدیل های یکسان پیامدهای تعاریف و ویژگی های اقدامات مربوطه است.

دستگاه دگرگونی‌های هویتی که در سال‌های گذشته انباشته شده است، در کلاس ششم گسترش یافته است. این بسط با معرفی هویتی آغاز می شود که ویژگی محصول قدرت ها را با پایه های یکسان بیان می کند:

مفهوم درجه با توان منطقی. حل معادلات غیر منطقی تابع نمایی، خواص و نمودار آن. تبدیلات یکسان عبارات نمایی. حل معادلات نمایی و نامساوی. لگاریتم یک عدد. ویژگی های اصلی لگاریتم ها تابع لگاریتمی، خواص و نمودار آن. حل معادلات لگاریتمی و نامساوی. مشتق تابع نمایی. عدد و لگاریتم طبیعی مشتق تابع توان.

هدف اصلی بخش تابع نمایی و لگاریتمی آشنایی دانش آموزان با توابع نمایی، لگاریتمی و توان است. حل معادلات و نابرابری های نمایی و لگاریتمی را به دانش آموزان آموزش دهید.

مفاهیم ریشه هفتم و درجه با توان گویا تعمیم مفاهیم ریشه دوم و درجه با توان صحیح است. دانش‌آموزان باید به این نکته توجه داشته باشند که ویژگی‌های ریشه‌ها و توان‌ها با توان‌های گویا در اینجا مشابه ویژگی‌هایی است که ریشه‌های مربعی قبلاً مطالعه شده و توان‌هایی با توان‌های صحیح دارند. لازم است زمان کافی برای تمرین ویژگی های درجه ها و توسعه مهارت های دگرگونی هویت اختصاص داده شود. مفهوم درجه با توان غیرمنطقی بر مبنای بصری و شهودی معرفی شده است. این ماده نقش کمکی ایفا می کند و هنگام معرفی تابع نمایی استفاده می شود.

مطالعه خواص توابع نمایی، لگاریتمی و توانی مطابق با طرح کلی پذیرفته شده برای مطالعه توابع ساخته شده است. در این مورد، یک نمای کلی از ویژگی ها بسته به مقادیر پارامتر ارائه می شود. نابرابری های نمایی و لگاریتمی بر اساس ویژگی های مورد مطالعه توابع حل می شوند.

یکی از ویژگی های دوره، سیستم سازی و تعمیم دانش دانش آموزان، تثبیت و توسعه مهارت های به دست آمده در دوره جبر است که هم هنگام مطالعه مطالب جدید و هم در طول تکرار کلی انجام می شود.

مسئله B7 بیانی می دهد که باید ساده شود. نتیجه باید یک عدد منظم باشد که بتوان آن را در برگه پاسخنامه شما یادداشت کرد. تمام عبارات به طور معمول به سه نوع تقسیم می شوند:

1. لگاریتمی،
2. نشان دهنده،
3. ترکیب شده.

عبارات نمایی و لگاریتمی در شکل خالص خود عملاً هرگز یافت نمی شوند. با این حال، دانستن نحوه محاسبه آنها کاملاً ضروری است.

به طور کلی، مشکل B7 کاملاً ساده حل می شود و کاملاً در حد توانایی های یک فارغ التحصیل متوسط ​​است. فقدان الگوریتم های واضح با استانداردسازی و یکنواختی آن جبران می شود. شما می توانید به سادگی از طریق آموزش زیاد حل چنین مشکلاتی را یاد بگیرید.

عبارات لگاریتمی

اکثریت قریب به اتفاق مسائل B7 شامل لگاریتم در یک شکل یا شکل دیگر است. این موضوع به طور سنتی دشوار در نظر گرفته می شود، زیرا مطالعه آن معمولاً در کلاس یازدهم رخ می دهد - عصر آمادگی انبوه برای امتحانات نهایی. در نتیجه، بسیاری از فارغ التحصیلان درک بسیار مبهمی از لگاریتم دارند.

اما در این کار هیچ کس به دانش نظری عمیق نیاز ندارد. ما فقط با ساده ترین عباراتی روبرو خواهیم شد که نیاز به استدلال ساده دارند و به راحتی می توان به طور مستقل بر آنها مسلط شد. در زیر فرمول های اساسی وجود دارد که برای مقابله با لگاریتم ها باید بدانید:

علاوه بر این، شما باید بتوانید ریشه ها و کسرها را با توانی با توان گویا جایگزین کنید، در غیر این صورت در برخی عبارات به سادگی چیزی برای خارج کردن از زیر علامت لگاریتم وجود نخواهد داشت. فرمول های جایگزین:

وظیفه. معنی عبارات را بیابید:
log 6 270 − log 6 7.5
log 5 775 − log 5 6.2

دو عبارت اول به عنوان تفاضل لگاریتم تبدیل می شوند:
log 6 270 − log 6 7.5 = log 6 (270: 7.5) = log 6 36 = 2;
log 5 775 − log 5 6.2 = log 5 (775: 6.2) = log 5 125 = 3.

برای محاسبه عبارت سوم، باید قدرت ها را جدا کنید - هم در پایه و هم در استدلال. ابتدا بیایید لگاریتم داخلی را پیدا کنیم:

سپس - خارجی:

ساختارهای فرم log a log b x برای بسیاری پیچیده و اشتباه به نظر می رسد. در همین حال، این فقط یک لگاریتم لگاریتم است، یعنی. log a (log b x ). ابتدا لگاریتم داخلی محاسبه می شود (log b x = c) و سپس خارجی: log a c.

عبارات نمایشی

ما یک عبارت نمایی را به هر ساختی از شکل k می‌گوییم، که در آن اعداد a و k ثابت دلخواه هستند و a > 0. روش‌های کار با چنین عباراتی بسیار ساده هستند و در درس‌های جبر کلاس هشتم مورد بحث قرار می‌گیرند.

در زیر فرمول های اساسی وجود دارد که قطعاً باید بدانید. استفاده از این فرمول ها در عمل، به عنوان یک قاعده، مشکلی ایجاد نمی کند.

1. a n · a m = a n + m ;
2. a n / a m = a n − m ;
3. (a n) m = a n · m ;
4. (a · b ) n = a n · b n ;
5. (a : b ) n = a n : b n .

اگر با یک عبارت پیچیده با قدرت مواجه شدید و نحوه برخورد با آن مشخص نیست، از یک تکنیک جهانی استفاده کنید - تجزیه به عوامل ساده. در نتیجه، اعداد زیاد در پایه های قدرت با عناصر ساده و قابل فهم جایگزین می شوند. سپس تنها چیزی که باقی می ماند این است که فرمول های فوق را اعمال کنید - و مشکل حل خواهد شد.

وظیفه. مقادیر عبارات را بیابید: 7 9 · 3 11: 21 8, 24 7: 3 6: 16 5, 30 6: 6 5: 25 2.

راه حل. بیایید همه پایه های قدرت ها را به عوامل ساده تجزیه کنیم:
7 9 3 11: 21 8 = 7 9 3 11: (7 3) 8 = 7 9 3 11: (7 8 3 8) = 7 9 3 11: 7 8: 3 8 = 7 3 3 = 189.
24 7: 3 6: 16 5 = (3 2 3) 7: 3 6: (2 4) 5 = 3 7 2 21: 3 6: 2 20 = 3 2 = 6.
30 6: 6 5: 25 2 = (5 3 2) 6: (3 2) 5: (5 2) 2 = 5 6 3 6 2 6: 3 5: 2 5: 5 4 = 5 2 3 2 = 150 .

وظایف ترکیبی

اگر فرمول ها را بدانید، پس تمام عبارات نمایی و لگاریتمی را می توان به معنای واقعی کلمه در یک خط حل کرد. با این حال، در مسئله B7 توان ها و لگاریتم ها را می توان با هم ترکیب کرد تا ترکیبات کاملاً قوی ایجاد کند.